Національний Технічний університет України (КРІ)

Кафедра теоретичної електротехніки

Лабораторна робота №14

з дисципліни "Основи електротехніки та електроніки"

"Дослідження лінійних кіл операторним методом"

Київ —2012

Мета роботи: Оволодіти методами аналізу і отримати навички експериментального лінійних кіл операторним методом

Розрахункова частина

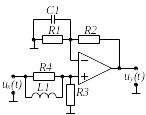
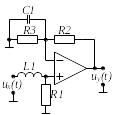
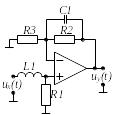
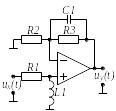
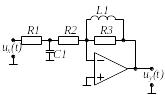
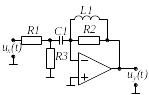
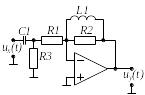
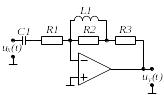
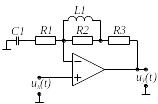
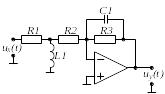
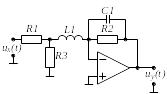
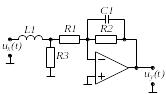
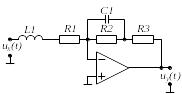
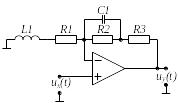
1. Вибрати відповідно до заданого викладачем варіанту N , який визначається номером студента у журналі групи, електричне коло (двополюсник) на стор. .

2. Обчислити параметри елементів електричного кола за N — номером студента у журналі групи і за індексом групи G за такими формулами:

Ом Ом Ом Ом Ом

Генрі Фарад

3. Скласти операторну схему заміщення заданого електричного кола

4. Знайти операторну передаточну функцію для струму в індуктивності

5. Обчислити нулі і полюси цієї функції

6. Знайти операторну передаточну функцію для струму в індуктивності

7. Обчислити нулі і полюси цієї функції

Результати обчислень записати у табл. 1.

Таблиця 1

	Моменти часу
	0	m	2m	3m	4m	5m
Струм в індуктивності
Результати обчислень
Результати вимірювань
Напруга на ємності
Результати обчислень
Результати вимірювань

Експериментальна частина Послідовність виконання роботи

1. Побудувати засобами Electronic Workbench електричне коло, відповідно до свого варіанту. Як приклад, на рис. 1 наведене електричне коло одного з варіантів.

2. Задати значення параметрів елементів кола, обчислені у пункті 2 розрахункової частини.

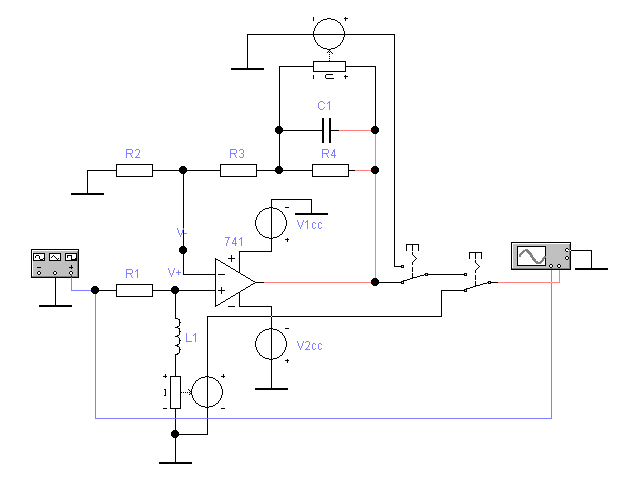
Рис.1

На рис. 1 показані:

Функціональний генератор, призначений для генерування послідовності імпульсів синусоїдної, трикутної і прямокутної форми;

Осцилограф, призначений для відображення графіків величин;

R1 — резистор;

L1 — індуктивний елемент;

С1 — конденсатор;

V_V1, V_V2, V_V3, V_V4 — керовані напругою джерела напруги;

I_V1 — кероване струмом джерело напруги;

SW1, SW2, SW3 — комутатори (ключі).

При роботі з осцилографом дотримуватися таких рекомендацій:

• Масштаб за часом (Time base) встановити такий, щоб на екрані осцилографа розміщувалося 1,5…2 періоди коливань.

• Запуск осцилографа (Triger) встановити від зовнішнього сигналу (Ext), наростанням імпульсу з нулевим (0,0) рівнем запуску (Level).

• Масштаб напруг у каналі А (Chanel A) і у каналі В (Chanel В) встановити такий, щоб подвійна амплітуда коливань становила не менше 3/4 екрану.

Варіант 1	Варіант 2
Варіант 3	Варіант 4
Варіант 5	Варіант 6
Варіант 7	Варіант 8
Варіант 9	Варіант 10
Варіант 11	Варіант 12
Варіант 13	Варіант 14
Варіант 15	Варіант 16

Теоретичні відомості

5.3 Операторний метод аналізу електричних кіл

Аналіз електричних кіл операторним методом ґрунтується на використанні інтегрального перетворення Лапласа. Застосування перетворення Лапласа для аналізу електричних кіл неперіодичного змінного струму і перехідних процесів у цих колах дає змогу перейти від розв’язування диференціальних рівнянь до розв’язування алгебраїчних рівнянь.

Інтегральне перетворення Лапласа ставить у взаємно однозначну відповідність функції f(t) функцію F(p) комплексного аргументу р відповідно до формули

. (5.141)

Функція f(t) називається оригіналом, а функція F(p) — зображенням. У електротехніці і електроніці оригіналами є струми, напруги, електрорушійні сили. Часто запис співвідношення (5.141) спрощують, користуючись умовним позначенням L[] інтегрального перетворення Лапласа

. (5.142)

Зображення найпростіших функцій. Користуючись інтегральним перетворенням Лапласа, можна показати, що зображення найпростіших функцій мають такий вигляд:

постійної величини ;	(5.143)
експоненціальної функції ;	(5.144)
синусоїдної функції ;	(5.145)
косинусоїдної функції ;	(5.146)
комплексне діюче значення синусоїдної функції .	(5.147)

Зображення похідної функції і інтеграла функції. Користуючись властивостями інтегрального перетворення, можна показати, що зображення похідної функції зв’язано із зображенням самої функції простим співвідношенням

. (5.148)

Зображення інтеграла функції зв’язано із зображенням самої функції співвідношенням

. (5.149)

Обернене перетворення Лапласа. Обернене перетворення Лапласа дає змогу за відомим зображенням F(p) знайти оригінал f(t) і записується у формі

; (5.150)

Обернене перетворення Лапласа позначається L^-1[], тобто

; (5.151)

Зображення більшості фізичних сигналів, зокрема більшість зображень сигналів у електричних і електронних колах мають вигляд

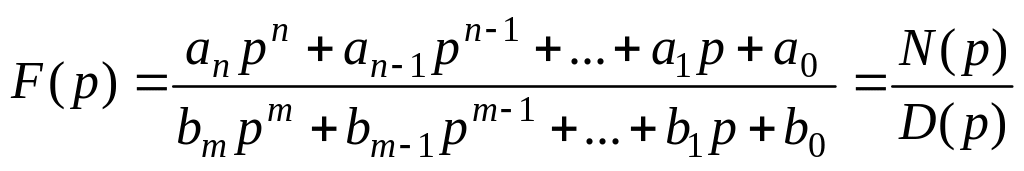, (5.152)

причому .

Можна довести, що обернене перетворення Лапласа від зображення, що виражається відношенням двох поліномів (5.152), записується у формі

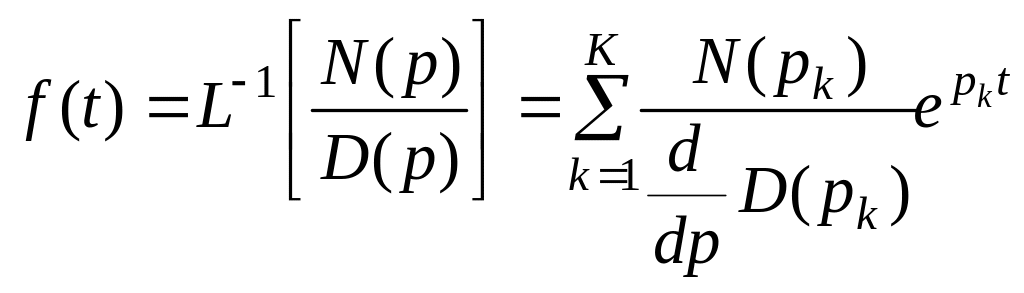; (5.153)

де p_k — корені полінома D(p).

Формула (5.153) носить назву теореми розкладання.

Приклад 5.2. Визначити оригінал, якщо зображення вихідного сигналу (вихідної напруги) електронного пристрою має вигляд

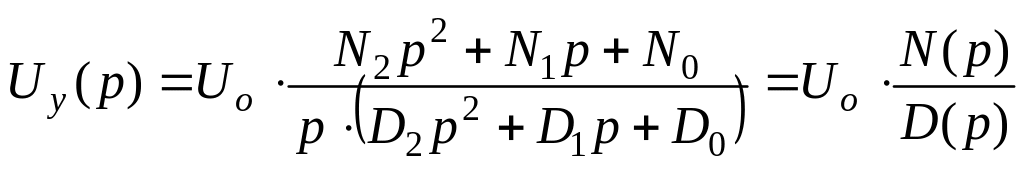. (5.154)