15) Законы радиоактивного распада ядер

    Способность ядер самопроизвольно распадаться, испуская частицы, называется радиоактивностью. Радиоактивный распад  - статистический процесс. Каждое радиоактивное ядро может распасться в любой момент и закономерность наблюдается только в среднем, в случае распада достаточно большого количества ядер.  Постоянная распада λ - вероятность распада ядра в единицу времени.      Если в образце в момент времени t имеется N радиоактивных ядер, то количество ядер dN, распавшихся за время dt пропорционально N.

dN = -λNdt.

(1)

Проинтегрировав (1) получим закон радиоактивного распада

N(t) = N0e-λt.

(2)

N₀ - количество радиоактивных ядер в момент времени t = 0. Cреднее время жизни τ -

.

(3)

Период полураспада T_1/2 - время, за которое первоначальное количество радиоактивных ядер уменьшится в два раза

T1/2 = ln2/λ=0.693/λ = τln2.

(4)

Активность A - среднее количество ядер распадающихся в единицу времени

A(t) = λN(t).

(5)

Активность измеряется в кюри (Ки) и беккерелях (Бк)

1 Ки = 3.7·10¹⁰ распадов/c, 1 Бк = 1 распад/c.

16) Радиоактивные ряды (семейства) — цепочки радиоактивных превращений.

Выделяют три естественных радиоактивных ряда и один искусственный.

Естественные ряды:

• ряд тория (4n) — начинается с нуклида Th-232;

• ряд радия (4n+2) — начинается с U-238;

• ряд актиния (4n+3) — начинается с U-235.

Искусственный ряд:

• ряд нептуния (4n+1) — начинается с Np-237.

После альфа- и бета-радиоактивных превращений ряды заканчиваются образованием стабильных изотопов.

17) Вероятности электромагнитных переходов

    Вероятности излучения γ-квантов возбужденными ядрами зависят от энергии E излучаемого кванта и от его мультипольности J – т.е. полного момента количества движения. По соотношению четности и мультипольности различают два типа γ-излучения:

электрическое (EJ), для которого четность P = (-1)J ; магнитное (MJ), для которого четность P = (-1)J+1.

(5.3)

    Точные выражения для вероятностей излучения γ-кванта ядром весьма сложны, в них, помимо энергии (или длины волны излучаемого кванта) и мультипольности излучения входят также квадраты матричных элементов операторов перехода между начальным и конечным состояниями ядра.      Если длины волн излучаемых (или поглощаемых) γ-квантов много больше, чем размеры излучателя (атомного ядра), то для приближенных оценок соотношений вероятностей γ-переходов можно использовать следующую зависимость вероятностей от мультипольности и длины волны излучаемого γ-кванта:

(5.4)

18)

19) Свойства нейтронов

Нейтрон является электрически нейтральной элементарной частицей, одной из составных частей ядра атома, с массой почти в 2000 раз тяжелее электрона. Время жизни нейтрона как свободной частицы около 15 минут, несмотря на то, что в связанном состоянии в ядре атома нейтрон является стабильной частицей.

 

Основные свойства нейтронов, применяемые в нейтронном рассеянии:

1.      Энергия замедленных нейтронов сравнима с энергией атомных и молекулярных движений, и находится в диапазоне от мэВ до эВ.

2.      Длина волны замедленных нейтронов сравнима с межатомными расстояниями, что позволяет исследовать структуру вещества в диапазоне 10^-5 – 10⁵ Å.

3.      Поскольку нейтроны являются нейтральными частицами, они взаимодействуют с ядрами атомов, а не с диффузными электронными оболочками. Сечение рассеяния нейтронов на близких по массе ядрах может существенно отличаться, это дает возможность «видеть» легкие ядра на фоне тяжелых, эффективно применять метод изотопного замещения, легко различать соседние элементы. Эта особенность является большим преимуществом перед методом рентгеновского рассеяния, в котором излучение рассеивается на электронной оболочке атомов.

4.      наличие магнитного момента у нейтронов позволяет изучать микроскопическую магнитную структуру и магнитные флуктуации, которые определяют макроскопические параметры вещества.

5.      Нейтронное излучение является глубоко проникающим вглубь вещества, что позволяет проводить исследования микроскопических свойств, типа микротрещин, промышленных объектов. Подобные исследования невозможно выполнить с помощью оптических методов, рентгеновского рассеяния или электронной микроскопии.

6.      Нейтроны являются безвредным, неповреджающим излучением даже в случае исследования живых биологических систем.

20)

21)

22)

23) Ядерное эффективное сечение, эффективное сечение ядра, ядерное сечение реакции, микроскопическое сечение реакции — величина, характеризующаявероятность взаимодействия частицы с ядром. Единица измерения эффективного сечения — барн (1 барн = 10⁻²⁸м²). С помощью известных эффективных сечений вычисляют скорости ядерных реакций или количества прореагировавших частиц.

Эта величина с одной стороны имеет тот же физический смысл, что и в классической механике, то есть эффективное сечение — это площадь поперечного сечения такой области пространства около частицы-мишени, при пересечении которой бомбардирующей частицей-точкой со 100 % вероятностью возникает взаимодействие, но при этом имеются существенные различия:

• ни в пределах объёма ядра, ни вблизи элементарной частицы нет такой области, при пересечении которой другой частицей обязательно произойдёт взаимодействие. Эффективное сечение просто даёт то число взаимодействий, которое в зависимости от его величины должно произойти. При этом в некоторых случаях даже при пересечении бомбардирующей частицей области эффективного сечения взаимодействия не происходит, тогда как в других случаях взаимодействие происходит, несмотря на пролёт частицы за пределами области эффективного сечения.

• эффективные сечения определяются не столько геометрическими размерами сложных микрочастиц или радиусами действия сил, сколько волновыми свойствами частиц. При возникновении связанных состояний область пространства, занятая взаимодействующей частицей, имеет радиус порядка дебройлевской длины волны 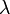 , а следовательно, сечение порядка  . Поскольку   обратно пропорциональна скорости, сечение возрастает при убывании энергии. Однако связанные состояния образуются при строгих энергетических соотношениях, и отвечающие им сечения наблюдаются только при избранных значениях энергии, что приводит к очень сложной картине поведения сечений в функции энергии.

Таким образом, эффективное сечение — это усреднённая по многим случаям взаимодействия величина, которая определяет прежде всего эффективность взаимодействия сталкивающихся частиц и только при определённых условиях даёт представление об их размерах или радиусах действия. В нейтронной физике эта величина также называется нейтронным эффективным сечением^[1].

Большинство сечений ядерных реакций имеют значения от 10⁻²⁷ до 10⁻²³см², то есть порядка геометрических сечений ядер, однако есть реакции, сечения которых много больше геометрических сечений ядра (порядка 10⁻¹⁸см²) и реакции, к примеру под действием медленных заряженных частиц, имеющие сечения много меньше геометрических сечений^[2].

24) Скорость ядерной реакции можно охарактеризовать средней продолжительностью т бомбардировки данного ядра мишени частицами до того момента, когда это ядро вступает в реакцию. [1]

Определение скоростей ядерных реакций является центральным моментом при расчете накопления того или иного радионуклида в реальных условиях облучения. [2]

Так как скорость ядерных реакций этого типа возрастает с повышением концентрации исходных веществ, особенно благоприятные условия для развития ядерных циклических превращений мы имеем в звездах. Звезды являются, таким образом, теми лабораториями, где в основном за счет различных ядерных цепных процессов образуются элементы системы Менделеева. Следует отметить, что на основе развитых представлений принципиально возможно дать приближенную оценку соотношений между количествами различных элементов в рассматриваемой системе. Для этого необходимо с помощью основных уравнений для кинетики цепных процессов определить количество различных изотопов, возникающих в ходе цепных превращений. После этого, учитывая различную устойчивость возникших изотопов, принципиально возможно определить количество тех устойчивых изотопов, которые остались к рассматриваемому периоду времени. Практически, однако, решение такой задачи встречает серьезные трудности вследствие недостаточности имеющихся данных для установления типа циклов и условий их развития внутри различных звезд. [3]

При определении скоростей ядерных реакций теоретические исследования не дают точного ответа, ввиду отсутствия теории сильных взаимодействий необходимо использовать экспериментальные данные. Получение их в области низких энергий, интересных для астрофизики, часто весьма затруднительно. [4]

Оптимизация режимов облучения мишеней в реакторе требует анализа зависимости скоростей ядерных реакций от плотности потока и спектра нейтронов. [5]

25) В ядерном реакторе функционируют свободные нейтроны широкого диапазона кинетических энергий - от 10^-3 эВ до десятков МэВ. Для удобс­тва их различий они классифицируются на: - быстрые нейтроны (с кинетическими энергиями выше 0.1 МэВ); - промежуточные нейтроны (с энергиями 0.625эВ < E < 0.1МэВ); - медленные нейтроны (с энергиями ниже 0.625 эВ). Необходимость такой классификации обусловлена тем, что нейтроны различных кинетических энергий обладаютразличной склонностью к вступ­лению в одни и те же нейтронные реакции с ядрами одних веществ. *) По этой причине,  говоря о плотности нейтронов, следует всегда указывать, о нейтронах какой энергии идет речь. Математическая форма записи - n(E) - полностью отвечает этому:  указывается и величина плотности нейтронов, и величина их кинетической энер­гии. Ибо, поскольку в рассматриваемом единичном объёме, кроме нейтронов с энергией Е, обязательно есть ещё нейтроны самых различных энергий очень широкого диапазона, суммарная (интег­ральная) плотность нейтронов всех возможных энергий будет:  n = ∫₀^∞n(E)^. dE                                 (2.3.2) Особую часть медленных нейтронов составляют тепловые нейтроны - то есть нейтроны, находящиеся в кинетическом равновесии с ядрами среды, в которой они движутся. Поскольку энергетическое распределение молекул (а следовательно, и атомов, и ядер атомов) в их тепловом движении имеет вид спектра Л.Больцмана: N(E) = N_о ^.C ^.E exp(-E / kT), -  аналогичное распределение должны иметь в непоглощающей среде и тепловые нейтроны: раз они находятся в кинетическом равновесии с ядра­ми атомов среды, то каждой группе ядер, имеющих определенную энергию Е, должна соответствовать пропорциональная по численности группа нейтро­нов той же энергии. Поэтому энергетический спектр тепловых нейтронов – спектр Максвелла (Maxwell) - в непоглощающих средах формально описы­вается тем же выражением: n(E) = n_o C E exp(-E / kT)                           (2.3.3) где: n(E) - плотность тепловых нейтронов, имеющих энергии в элементар­ном интервале dE вблизи значения Е; n_o - интегральная плотность  тепловых  нейтронов  всех  возможных энергий в среде с термодинамической температурой Т; k = 8.62 ^.10^-5 эВ/К - постоянная Больцмана; С  - постоянный сомножитель нормировки. В реальной (поглощающей нейтроны) среде максвелловское распреде­ление тепловых нейтронов по энергиям, конечно, нарушается. Однако, ком­пактное математическое удобство этого выражения настолько велико, что условились считать, что и в поглощающей тепловые нейтроны среде энер­гетическое распределение тепловых нейтронов сохраняет ту же (гауссову) форму, что и в непоглощающей среде: n(E) = n_o C E exp(-E / kT_н),                                    (2.3.4) с той лишь разницей, что в показателе экспоненциала стоит не термодинамическая температура среды Т, а так называемая темпера­тура нейтронов Т_н. Максвелловский спектр тепловых нейтронов (рис.2.9) характеризует­ся следующими присущими ему энергиями тепловых нейтронов: а) Наиболее вероятной энергией Е_нв = kT_н, соответствующей макси­муму распределения тепловых нейтронов по энергиям при данной темпе­ратуре нейтронов Т_н. Это означает, что тепловых нейтронов с кинетичес­кой энергией Е_нв в среде больше, чем тепловых нейтронов любых других энергий (до 36% от общего числа всех тепловых нейтронов). б) Средней энергией тепловых нейтронов: Е_ср = (1/n_o) ∫₀^∞E n(E) dE                      (2.3.5) Подстановка в (2.3.5) выражения (2.3.4) приводит к величине: E_ср = 4kT_н / p ≈ 1.273 kT_н = 1.273 Е_нв                          (2.3.6) В частности при температуре нейтронов Т_н = 293К (или 20^оС), называемой стандартной температурой,наиболее вероятная и средняя энергии тепло­вых нейтронов соответственно равны: E_нв = 0.0253 эВ                   Е_ср = 0.0322 эВ Заметим одно счастливое свойство максвелловского спектра: Отношение средней и наиболее вероятной энергий нейтронов  в спектре Максвелла при постоянной температуре нейтронов  есть величина постоянная, равная Е_ср/Е_нв = 4/π ≈ 1.273. Cледовательно, отношение скоростей нейтронов, соответствующих средней и наиболее вероятной энергиям тепловых нейтронов: v_ср/v_нв = √4/π = 2/√π ≈ 1.128,                                       (2.3.7) - то есть также является постоянной величиной. Запомним это. Понятие средней энергии тепловых нейтронов понадобилось  нам  для того, чтобы поведение и взаимодействия всей совокупности различных по энергиям тепловых нейтронов заменить эквивалентным их взаимодействием с ядрами среды так, словно все они одинаковы по энергиям, а значит - и по своим свойствам. Суммирование кинетической энергии всех тепловых нейтронов и раздел этой суммы поровну между всеми тепловыми нейтронами - см. формулу (2.3.5) - как раз и приводит к понятию "среднего теплово­го нейтрона", подобно понятию "среднего нейтрона деления", с которым мы уже имели дело,  говоря о спектре Уатта. Итак, спектр нейтронов, то есть их энергетическое распределение в среде, является второй характеристикой нейтронного поля. К сожалению, теория реакторов до сих пор не располагает компакт­ным аналитическим выражением для спектравсех нейтронов в реакторе, и поэтому задачу по выяснению реакторного спектра приходится решать путём громоздких вычислений с помощью ЭВМ. Частные же задачи теории решаются на базе трёх энергетических спектров: спектр нейтронов деления (Уатта); спектр тепловых нейтронов (Максвелла) и спектр замедляющихся нейтронов (Ферми), с которым мы познакомимся позже. 26) Макроскопическое сечение

Макроскопическое сечение   i-го процесса для j-го нуклида в среде можно определить как произведение i-го микроскопического сечения ядра этого нуклида   и ядерной плотности j-го нуклида  :

То есть макроскопическое сечение представляет собой как бы сечение всех ядер единицы объёма вещества. Правда такая трактовка довольно условна, так как из выражения видно, что оно не является собственно сечением и измеряется в 1/м. При описании прохождения потоков фотонов через вещество эту величину также называют линейным коэффициентом ослабления.

Используя представленное выше выражение эффективного сечения ядра для плоской мишени, можно дать другое определение макроскопического сечения:

 — это число взаимодействий i-го типа в единицу времени в единице объёма j-го нуклида при единичном   (то есть  ).

То есть если макроскопическое сечение представляет собой произведение концентрации ядер на какое-то парциальное микроскопическое сечение, например сечение рассеяния или захвата, то оно тоже будет парциальным и выражать скорость конкретных процессов в единице вещества, например число случаев рассеяния или поглощения нейтронов.

Ядерную плотность определяют по формуле:

, где:

 — число Авогадро,

 — атомная масса,

 — плотность вещества

Если вещество представляет собой гомогенную смесь различных ядер, то макроскопическое сечение смеси определяют как сумму макроскопических сечений веществ в смеси. При гетерогенном расположении материалов необходимо учитывать объёмную долю, занятую данным веществом  . Тогда ядерные плотности каждого вещества   домножают на на эту величину:

 (сумма   равна 1)

Необходимо отметить, что в случае гетерогенного расположения материалов сечение не всегда определяют как сумму сечений, так как различные материалы могут находиться в разных условиях^[1][2]. Микроскопические сечения

Теперь можно ввести в рассмотрение микросечения. Тогда

Величина носит название плотности потока нейтронов (в дальнейшем - поток) - и по физическому смыслу это число нейтронов, пересекающих единичную площадку за единицу времени.

В зависимости от вида взаимодействия рассматривают соответствующие микросечения. Для учета всех взаимодействий вводят понятие полного микросечения , которое для реакторных нейтронов складывается:

Однако удобно ввести другие обозначения. Так, все сечения рассеяния объединяют:

Макроскопические сечения

Макроскопическим сечением Σ называется произведение σ·N . Т.е. это результирующее эффективное сечение всех атомов, находящихся в 1 см³.

Ядерная плотность определяется следующей формулой:

Если вещество представляет собой гомогенную смесь j-ых нуклидов, то сечения смеси определяется как:

Ядерная плотность j-го компонента определяется его массовой концентрацией С_j и плотностью смеси ρ_смеси:

В случае сложных химических соединений массовая концентрация j-го элемента определяется числом атомов (k_j) j-го элемента, входящих в соединение и молекулярной массой соединение μ_мол, тогда N:

В гетерогенных системах необходимо учитывать объемную долю вещества. Кроме того, расположение материалов в различных условиях не всегда позволяет использовать аддитивный подход при определении сечения.