13. Некоторые частные случаи движения точки

Пользуясь полученными результатами, исследуем зависимость значений ее нормального и касательного ускорений от характера движения точки.

При равномерном движении, когда численное значение скорости    постоянно, касательное ускорение    обращается в нуль. Оно отлично от нуля только при неравномерном движении и поэтому характеризует изменение скорости по величине.

При прямолинейном движении, когда радиус кривизны траектории    равен бесконечности, нормальное ускорение обращается в нуль. Оно отлично от нуля только при криволинейном движении и, следовательно, характеризует изменение скоро­сти по направлению.

Обе составляющие ускорения обращаются в нуль только при равномерном и прямолинейном движении.

Неравномерное движение точки называется ускоренным, если модуль скоро­сти возрастает, и замедленным - в противоположном случае. Легко доказать, что движение является ускоренным, если знаки величин   и 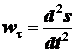   одинаковы, и замедленным, если эти знаки различны. При ускоренном движении вектор касательного ускорения направлен в ту же сторону, что и скорость, при замедленном - в противоположную сторону.

Движение называется равнопеременным в том случае, если касательное

ускорение постоянно, т. е.

  , (2.24)

 откуда

.

Интегрируя последнее выражение и имея в виду, что при     , полу­чим

. (2.25)

Формула (2.25) определяет скорость равнопеременного движения. Под­ставляем в нее значение  . Интегрируя и имея в виду, что при     , получим

  . (2.26)

 Выражение (2.26) называют уравнением равнопеременного движения точки по траектории.

14. Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д. 

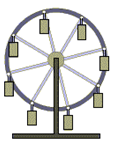
Рис. 1.1

Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

Доказательство. 

Если выбрать две точки твердого тела А  и В  (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением

Траектория точки А  – это кривая, которая задается функцией r_A(t), а  траектория точки B – это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени выражение

Получаем

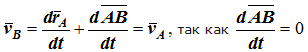
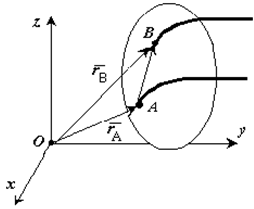
Рис. 1.2

Продифференцируем по времени скорость и получим выражение a_B = a_A. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

15. Вращательное движение тела в зависимости от времени t характеризуют угловые величины: φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек²).

Закон вращательного движения тела выражается уравнением  φ = f (t).

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени  ω = dφ/dt = f' (t).

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости  ε = dω/dt = f'' (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ_об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то  φ = 2πφ_об и φ_об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам  ω = πn/30 и n = 30ω/π.

При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a_t и a_n, характеризующими движение различных точек этого тела (рис 205).

Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:  s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством  v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой  a_t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью  a_n = ω²R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.

Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид  φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,  φ = ωt.

Угловую скорость равномерно вращающегося тела  ω = φ/t  можно выразить и так:  ω = 2π/T,  где T – период вращения тела; φ=2π – угол поворота за один период.

 Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным. Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения  (1)φ = φ₀ + ω₀t + εt²/2  и уравнение, выражающее угловую скорость тела в любой момент времени,  (2)ω = ω₀ + εt  представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:  (3)φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:  (4)φ = φ₀ + (ω² - ω₀²)/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:  (5)φ = εt²/2;  (6)ω = εt;  (7)φ = ωt/2;  (8)φ = ω²/(2ε).