1. Аксиомы (законы) статики: 1) аксиома инерции: Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.

2) аксиома равновесия двух сил: Две силы, приложенные к абсолютно твердому телу, будут уравновешены тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

3) аксиома присоединения и исключения уравновешивающихся сил: Действие системы сил на абс. твердое тело не изменится, если к ней прибавить или отнять уравновешенную систему сил. Следствие: Действие силы на абс.тв. тело не изменится, если перенести точку приложения силы вдоль ее линии действия. Т.е. сила, приложенная к абс.тв. телу– скользящий вектор.

4) аксиома параллелограмма сил: Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.

5) аксиома равенства действия и противодействия (3-й закон Ньютона): Всякому действию соответствует равное и противоположно направленное противодействие.

6) принцип отвердевания: Равновесие сил, приложенных к нетвердому телу, не нарушается при его затвердевании.

Абсолю́тно твёрдое те́ло — второй опорный объект механики наряду с материальной точкой. Механика абсолютно твёрдого тела полностью сводима к механике материальных точек (с наложенными связями), но имеет собственное содержание (полезные понятия и соотношения, которые могут быть сформулированы в рамках модели абсолютно твёрдого тела), представляющее большой теоретический и практический интерес.

2. Связи и реакции связей Тело называется свободным, если его перемещение в пространстве ничем не ограничено. В противном случае тело называется несвободным, а тела, ограничивающие перемещения данного тела, ¾ связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей. Основные виды связей и их реакции: 1.        Гладкая поверхность (без трения):

Реакция гладкой поверхности направлена по нормали к этой поверхности  (перпендикулярна общей касательной). 2. 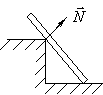       Опорная точка (ребро):Реакция перпендикулярна опирающейся поверхности.

3.       Идеальная нить (гибкая, невесомая, нерастяжимая): Примеры: моделирует трос, канат, цепь, ремень,… Реакция идеальной нити направлена по нити к точке подвеса.

4.       Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры):

Реакция связи направлена по стержню. В отличие от нити стержень может работать и на сжатие.

5.       Цилиндрический шарнир: Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вокруг оси шарнира, но не позволяет точке закрепления перемещаться в плоскости, перпендикулярной оси шарнира. Реакция лежит в плоскости, перпендикулярной оси шарнира, и проходит через нее. Положение этой реакции не определено, но она может быть представлена двумя взаимно перпендикулярными составляющими

6.       Сферический шарнир: Такая связь не дает точке закрепления тела перемещаться ни в одном из направлений. Положение  реакции не определено, но она может быть представлена тремя взаимно перпендикулярными составляющими.

7.       Подпятник: 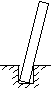Реакция данной связи задается аналогично предыдущему случаю.

8.      Жесткая заделка: Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая, как будет показано, может быть заменена одной силой и парой сил.

Аксиома освобождаемости от связей: Всякое несвободное тело можно считать свободным, если мысленно освободиться от связей, а их действие заменить соответствующими реакциями.

3. Проекция силы на ось

    Проекция силы на ось – это алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на соответствующие оси. Рисунок 1.13):

 F_x= Fcosα;

P_x= Pcosβ= P⋅ cos90^o=0;

R_x= Rcosγ = -R⋅ cos(180^o-γ).   

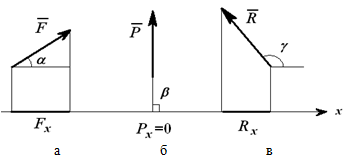
Рисунок 1.13

    Проекция силы на ось может быть положительной, рис. 1.13а (0 ≤ α < π/2), равной нулю, рис. 1.13б (β = π/2 ) и отрицательной, рис. 1.13в (π/2 < γ ≤ π).

    Иногда для нахождения проекции силы на ось сначала нужно найти ее проекцию на плоскость, а потом проекцию на ось (рисунок 1.14):

 P_z= P sinα;

P_x= (P cosα)cosβ;

Py= (P cosα)cosγ = P cosα⋅ cos(90^o-β).

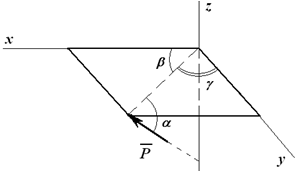
Рисунок 1.14

4. Сосре­доточенными считаются силы, приложенные к малой поверхности, размеры которой малы по сравнению с размерами тела. Однако при расчете напряжений вблизи зоны приложения силы нагрузку следует считать распределенной. К сосредоточенным нагрузкам относят не только сосредоточенные силы, но и пары сил, примером которых можно счи­тать нагрузку, создаваемую гаечным ключом при закручивании гайки. Сосредоточенные усилия измеряются в кН.

Распределенные нагрузки бывают распределенными по длине и по площади . К распределенным нагрузкам относят давление жидкости, газа или другого тела. Распределенные силы измеряются, как правило, в кН/м (распределенные по длине) и кН/м2 (распределенные по площади).

ИНТЕНСИВНОСТЬ НАГРУЗКИ нагрузка, приходящаяся на единицу нагруженной площади или длины

5.Сложение сходящихся сил. Система сил, линии действия которых пересекаются в одной точке,

называется системой с х о д я щ и х с я с и л.

Сложить две или несколько сил - это значит заменить эти силы одной силой, им эквивалентной, т.е.

найти их равнодействующую.

Из ADC: т.к.

Разложить силу — значит найти ее составляющие. Две равные силы, направленные по одной прямой в противоположные стороны, взаимно уравновешиваются, тело при действии этих сил находится в равновесии, т. е. в состоянии покоя.

6. Момент силы относительно центра (или точки).

Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее момен­том

Рассмотрим силу  , приложенную в точке А твердого тела (рис. 20). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы  , на­зывается плечом силы   от­носительно центра О. Так как точку приложения силы можно произвольно переме­щать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть: 1) от модуля силы F и длины плеча h; 2) от поло­жения плоскости поворота ОАВ, проходящей через центр О и силу F; 3) от направления поворота к этой плоскости.

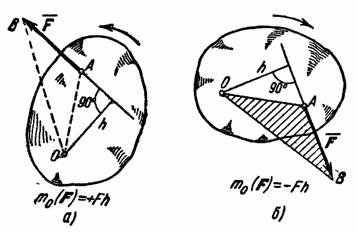
Рис.20

 

Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.

Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы   относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.

Момент силы   относительно центра О будем обозначать сим­волом m₀(F). Следовательно,

В дальнейшем условимся считать, что момент имеет знак плюс, если сила стремится повернуть тело вокруг центра О против хода ча­совой стрелки, и знак минус, - если по ходу часовой стрелки. Так, для силы  , изображенной на рис.20,а, момент относительно центра О имеет знак плюс, а для силы, показанной на рис.20,б, - знак ми­нус.

Отметим следующие свойства момента силы:

1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.

2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).

3) Момент силы численно выражается удвоенной площадью тре­угольника ОАВ (рис. 20,б)

Этот результат следует из того, что

7. Теорема Вариньона о моменте равнодействующей.

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил от­носительно любого центра равен алгеб­раической сумме моментов слагаемых сил относительно того же центра.

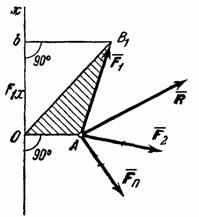
Рис.21

 

Рассмотрим систему сил  ,  , …,  , сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Для доказательства теоремы найдем соответствующие  выражения  моментов m₀( ), m₀( ), … . По формуле  . Но, как видно из рисунка,  , где F_1x - проекция силы   на ось Ох; сле­довательно  

.                                                                   

Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил  ,  , …,  , через  , где  . Тогда, по теореме о проекции суммы сил на ось, получим  . Умножая обе части этого равенства на ОА, найдем:

или,

.