1.1. Дифференциальное уравнение автогенератора

Анализ работы автогенератора проводят на основе решения его диф­ференциального уравнения, но сначала рассмотрим свободные колеба­ния в LС - контуре. Это необходимо сделать в связи с тем, что колеба­тельный контур является главным элементом автогенератора гармони­ческих колебаний, а источник постоянного тока, регулятор и цепь обратной связи - вспомогательными элементами, с помощью которых лишь компенсируются потери энергии в колебательном контуре. Для изучения физических процессов, происходящих в одиночном колебательном контуре, рассмотрим схему рис. 3, а

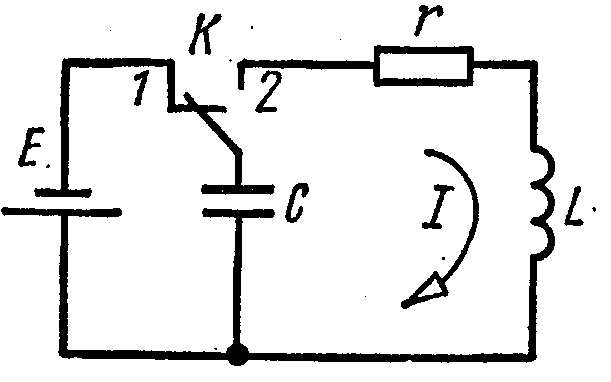
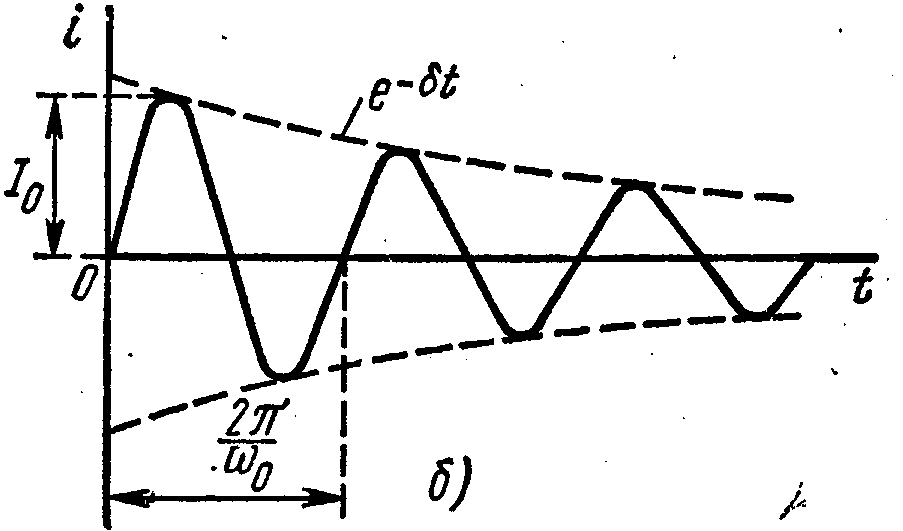
Рис. 3. Свободные колебания в LС - контуре:

а - принципиальная схема; б - временная диаграмма.

Сначала ключ K находится в положении 1 и в контуре происходит накопление энергии в виде заряда конденсатора С. Если в момент t = 0 перевести ключ K в положение 2, то в контуре возникнут свободные колебания, которые описываются дифференциальным уравнением

,

или после дифференцирования и деления на L

. (1)

Вводя обозначение , (δ - коэффициент затухания контура) и учитывая, что ,

последнее уравнение можно записать в окончательном виде:

. (2)

С учетом того, что в радиоэлектронике используются колебатель­ные контуры с малыми потерями, решение дифференциального урав­нения (2) будет иметь вид

, (3)

где I₀ - начальная амплитуда тока в колебательном контуре, завися­щая от запасенной контуром энергии, а ω_CB ≈ ω_P - частота свободных колебаний.

Свободные колебания в контуре будут иметь форму, показанную на рис. 3, б. Очевидно, в обычном контуре свободные колебания будут затухающими из - за наличия потерь (сопротивление г).

Теперь перейдем к автогенератору. Но прежде чем составлять его дифференциальное уравнение, отметим, что в зависимости от условий работы автогенератора необходимо учитывать разное число парамет­ров, характеризующих происходящие в нем процессы. Например, на низких частотах активный элемент автогенератора можно считать безынерционным и имеющим очень большое входное сопротивление, что приводит к простому дифференциальному уравнению. При увеличении генерируемой частоты следует учитывать величину входного сопротив­ления и инерционность активного элемен­та, что усложняет дифференциальное урав­нение. Ограничимся простейшим случаем и составим дифференциальное уравнение для транзисторного автогенератора с транс­форматорной связью (рис. 4), предпола­гая, что частота генерируемых колебаний. достаточно низка и можно не учитывать инерционные свойства транзистора и величину его входного сопротивления. Для этой схемы справедливы следующие уравнения:

i_K(t) = i(t) + i_C(t)

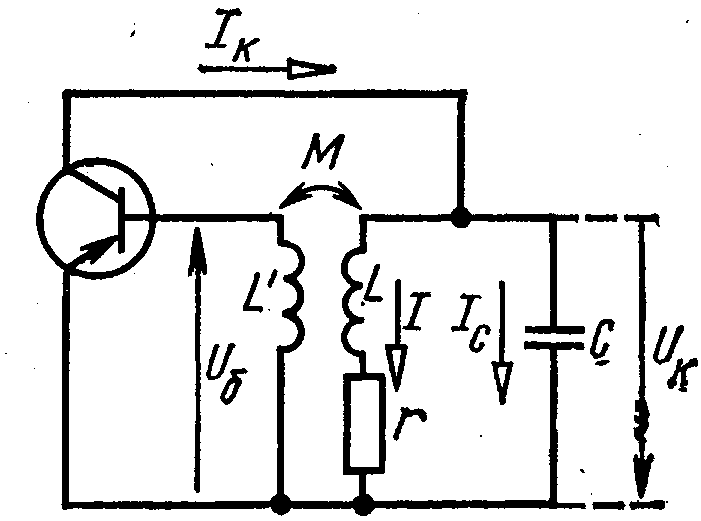
Рис. 4. Принципиальная схема по переменному току транзисторного LС - автогенератора

(4)

Заменив во втором уравнении (4) ток в емкостной ветви контура через ток в индуктивной ветви и коллекторный ток: i_C(t) = i_K(t) - i(t) и продифференцировав полученное выражение по времени, получим диф­ференциальное уравнение автогенератора для токов:

(5)

Поскольку в рассматриваемой схеме автогенератора существует обратная связь, на базе транзистора возникает переменное напряже­ние и₆, которое является функцией тока в индуктивной ветви контура:

U_В(t) = ± M

Знак «±» обусловлен тем, что катушка обратной связи может быть включена либо согласно, либо встречно по отношению к контурной катушке L. Коллекторный ток i_к транзистора в общем случае является нели­нейной функцией напряжений и_б и и_к. Однако во многих случаях в схеме рис. 4.4 транзистор работает в режиме, когда напряжение и_к мало влияет на ток i_к. Поэтому для упрощения можно пренебречь вли­янием напряжения на коллекторе и считать, что коллекторный ток за­висит только от напряжения на базе:

i_K(t) = Ψ(U_B). (6)

Тогда уравнение (5) принимает вид

(7)

или после преобразования правой части

M = M = M = Mφ((u_B(t)) . (8)

Подставляя в правую часть уравнения (7) выражение (8), про­ведя элементарные преобразования и опуская в дальнейшем индекс «б», получим основное уравнение автогенератора:

. (9)

Это нелинейное дифференциальное уравнение второго порядка, точного решения которого в настоящее время не существует. Поэтому в теории автогенераторов приходится пользоваться приближенными методами. При этом для исследования одних вопросов используют ме­тоды грубого приближения, для других - достаточно точные. Наиболее грубым приближением является линеаризация уравне­ния (4.9), которая применяется для определения условий самовозбуждения автогенератора. Более точным является квазилинейный ме­тод, позволяющий решить задачу об амплитуде и частоте стационар­ных колебаний автогенератора. И, наконец, для ответа на вопрос о поведении автогенератора в любой момент времени приходится ис­пользовать наиболее точные методы решения нелинейных дифференци­альных уравнений, например метод медленно меняющихся амплитуд (метод Ван – дер – Поля). Далее исследуются основные режимы работы автогенераторов.