2. Экономико-математическая модель задачи

Данная задача является транспортной задачей линейного программирования. Проверим, совпадают ли суммарные запасы муки на складах с суммарными потребностями в ней магазинов:

• суммарные запасы муки на складах

тонн;

• суммарные потребности магазинов

тонн.

Видно, что суммарные запасы муки на складах превышают суммарные потребности магазинов:

.

Следовательно, транспортная задача является открытой, и решать такую задачу будем путем приведения ее к закрытой задаче. Для этого вводится фиктивный потребитель E, потребность которого равна разности между суммарными запасами муки на складах и суммарными потребностями магазинов:

тонн.

Стоимость перевозки единицы груза фиктивному потребителю принимается равной нулю, так как груз фактически не перевозится.

Представим исходные данные закрытой задачи в виде таблицы:

Мощности поставщиков ai (i=1, …, 4)	Мощности потребителей bj (j=1, …, 5)
	40	20	75	110	25
70	4	4	5	8	0
80	2	5	7	7	0
30	1	2	5	6	0
90	4	6	6	8	0

В ячейках с заливкой находятся удельные транспортные затраты на перевозку одной тонны муки c_ij от i–го поставщика к j–му потребителю.

Обозначим через x_ij количество муки (в тоннах), запланированное к перевозке с i–го склада в j–й магазин. Стоимость такой перевозки составит , а математическая модель задачи будет иметь вид:

Найти такие значения x_ij, чтобы общая стоимость перевозок была наименьшей:

;

и при этом:

 вся имеющаяся на складах мука должна быть перевезена:

;

 все потребности магазинов в муке должны быть удовлетворены:

;

 перевозимые количества не могут быть отрицательными:

.

3. Компьютерная технология получения оптимального решения

Данную задачу решаем с помощью надстройки «Поиск решения» табличного процессора EXCEL. В ячейки рабочего листа программного средства вводятся исходные данные и формулы:

• В ячейки А5:A8 вводятся мощности поставщиков, в ячейки B4:F4 — мощности потребителей, в ячейки B5:F8 — значения удельных транспортных затрат на перевозку одной тонны муки.

• В ячейках B12:F15 находятся значения переменных x_ij (i=1, …, 4; j=1, …, 5). Первоначально в них помещаются произвольные числа, например, единицы.

• В ячейки А12:A15 вводятся формулы для расчета сумм значений переменных в соответствующих строках. Например, в ячейке A12 формула имеет вид: =СУММ(B12:F12).

• В ячейки B11:F11 вводятся формулы для расчета сумм значений переменных в соответствующих столбцах. Например, в ячейке B11 формула имеет вид: =СУММ(B12:B15).

• В ячейку B18 вводится выражение целевой функции задачи с использованием встроенной функции «СУММПРОИЗВ». Аргументами этой функции являются блоки ячеек, содержащие удельные транспортные затраты и значения переменных: =СУММПРОИЗВ(B5:F8;B12:F15).

Исходный рабочий лист EXCEL, таким образом, имеет вид:

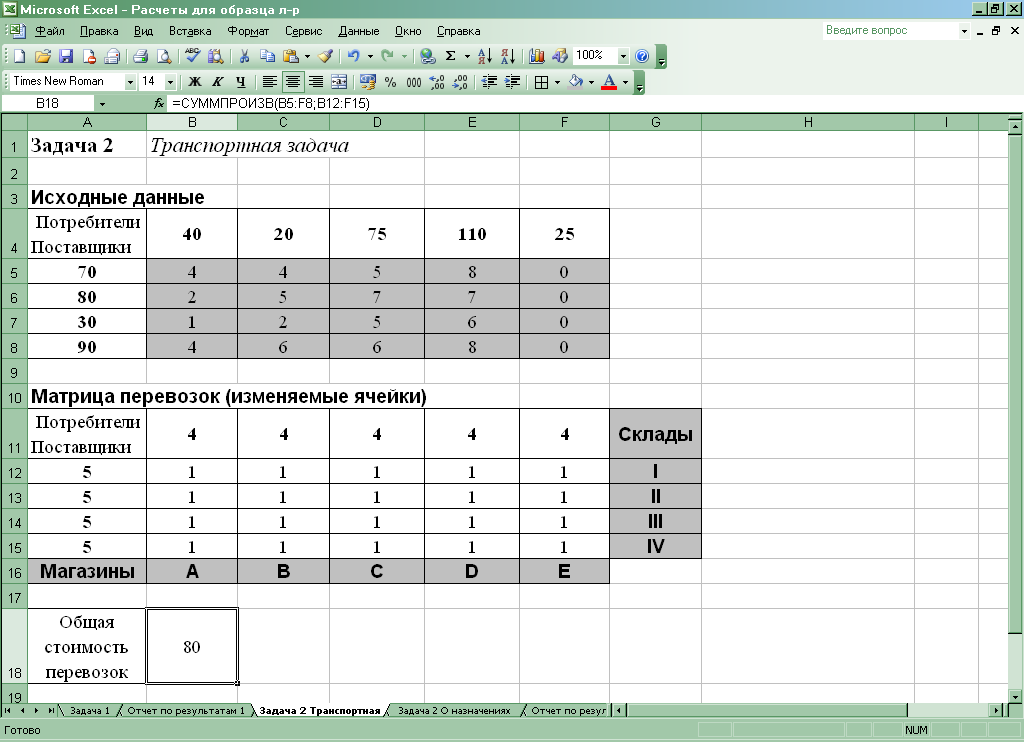
После ввода исходных данных запускается надстройка «Поиск решения» (меню «Сервис») и заполняются все необходимые поля в панели надстройки:

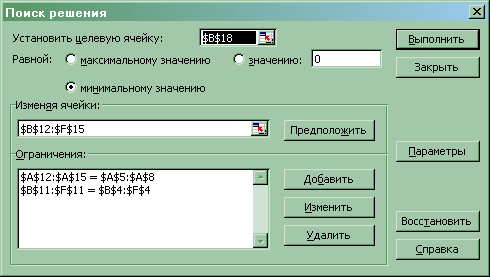
В панели «Параметры поиска решения» указывается, что модель задачи оптимизации является линейной, и задается условие неотрицательности переменных: