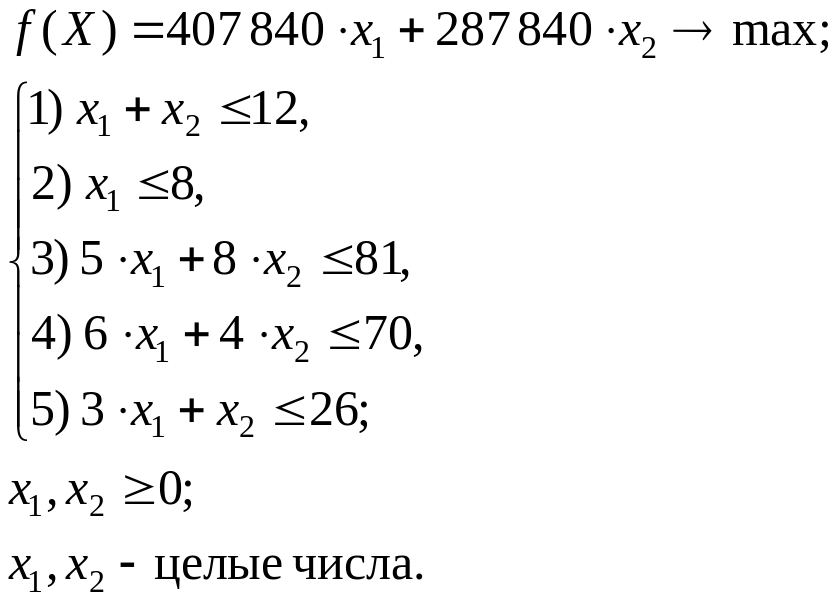16

Министерство образования и науки Российской Федерации

Федеральное государственного бюджетное образовательного учреждения высшего профессионального образования

Финансовый Университет при правительстве РФ

Брянский филиал

ЛАБОРАТОРНАЯ РАБОТА

по дисциплине

Методы принятия управленческих решений

Вариант 11

ВЫПОЛНИЛ(А)	Симонова Н.С.
СТУДЕНТ(КА)	2 курса
НАПРАВЛЕНИЕ	МЕНЕДЖМЕНТ (день)
№ ЗАЧ. КНИЖКИ	07ММД15027
ПРЕПОДАВАТЕЛЬ	Дадон В.А.

Брянск — 2012

ЗАДАЧА 1

Оптимальное формирование поездов

1. Постановка экономической задачи (исходные данные варианта)

Из пункта А в пункт В ежедневно отправляются пассажирские и скорые поезда. В таблице указаны наличный парк вагонов разных типов, из которых можно комплектовать данные поезда, количество пассажиров, вмещающихся в каждый из вагонов, и стоимость билета на проезд:

Поезда	Вагоны
	багажный	почтовый	плацкарт	купейный	мягкий
Скорый	1	1	5	6	3
Пассажирский	1	—	8	4	1
Число пассажиров	—	—	58	40	32
Парк вагонов	12	8	81	70	26
	Стоимость билета, руб.
Скорый	—	—	400	760	1140
Пассажирский	—	—	350	600	920

Какое количество скорых и пассажирских поездов следует отправлять ежедневно из пункта А в пункт В, чтобы обеспечивалась наибольшая выручка от продажи билетов при условии стопроцентной заполняемости поездов?

2. Экономико-математическая модель задачи

Данная задача является целочисленной задачей линейного программирования. Сформулируем целевую функцию задачи. Обозначим через х₁ количество скорых, а через х₂ — пассажирских поездов, перемещающихся ежедневно из пункта А в пункт В. Пассажиры перевозятся в плацкартных, купейных и мягких вагонах, количество мест в которых составляет соответственно: 58, 40 и 32.

Скорый поезд включает в себя 5 плацкартных, 6 купейных и 3 мягких вагона. Стоимость билета в плацкартном, купейном и мягком вагонах скорого поезда составляет соответственно 400, 760 и 1140 руб. Таким образом, при стопроцентной заполняемости скорого поезда выручка от реализации всех билетов на проезд в нем составит: руб. Общая ежедневная выручка от реализации билетов на все скорые поезда составит руб.

Пассажирский поезд включает в себя 8 плацкартных, 4 купейных, 1 мягкий вагон. Стоимость билета в плацкартном, купейном и мягком вагонах пассажирского поезда составляет соответственно 350, 600 и 920 руб., а выручка от реализации всех билетов на пассажирский поезд — руб. Общая ежедневная выручка от реализации билетов на все пассажирские поезда будет равна руб.

Суммарная выручка от реализации билетов на проезд во всех скорых и пассажирских поездах в день — руб., является целевой функцией задачи, которую необходимо максимизировать. Окончательно целевая функция имеет вид:

.

Сформируем систему ограничений на изменение значений переменных х₁ и х₂. Имеются пять ограничений по количеству вагонов разного типа:

• Парк багажных вагонов составляет 12 штук. И скорый, и пассажирский поезда включают в себя по одному багажному вагону. Следовательно ограничение по парку багажных вагонов будет иметь вид: 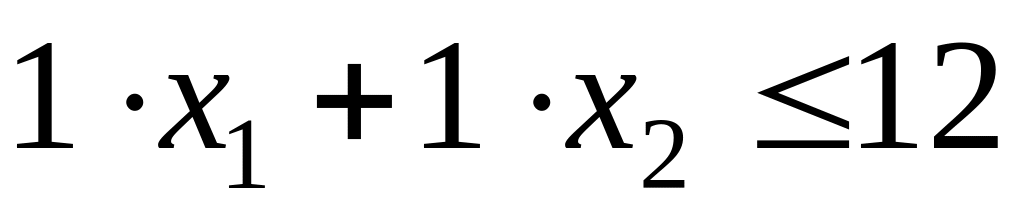, или, что одно и тоже — .

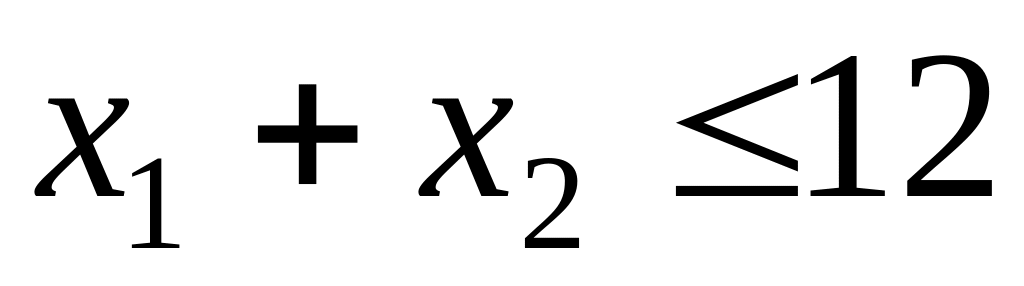• Всего имеется 8 почтовых вагонов. Скорый поезд включает в себя 1 почтовый вагон, пассажирские поезда почтовыми вагонами не комплектуются. Таким образом ограничение по парку почтовых вагонов выглядит следующим образом: 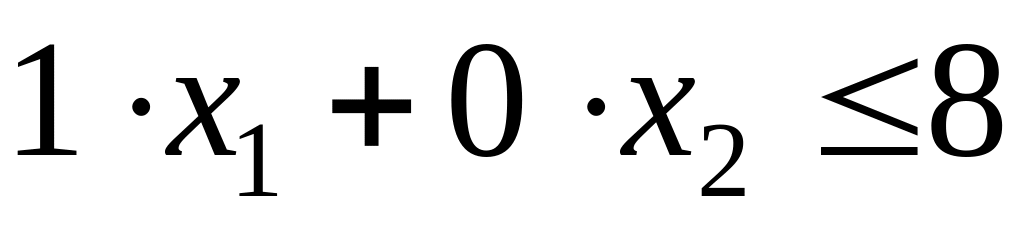, т.е. .

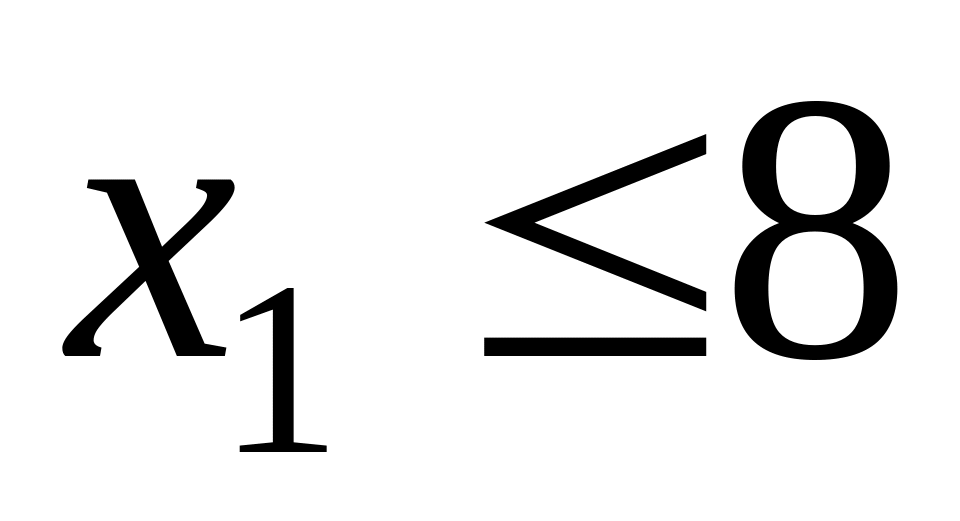Аналогичным образом формулируются и три других ограничения:

• по парку плацкартных вагонов — ;

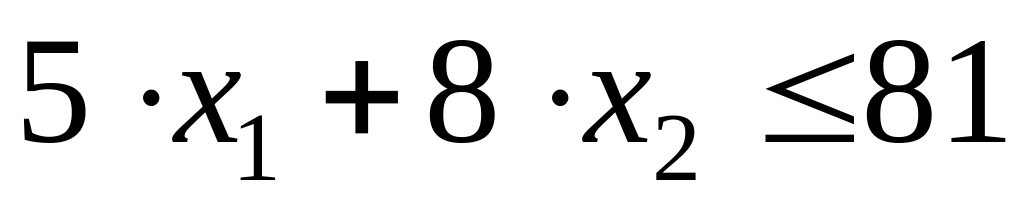• по парку купейных вагонов — ;

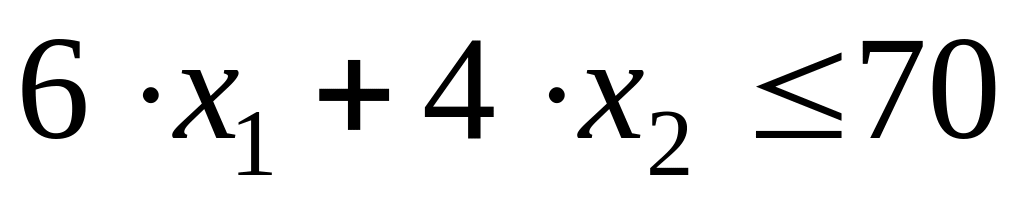• по парку мягких вагонов — 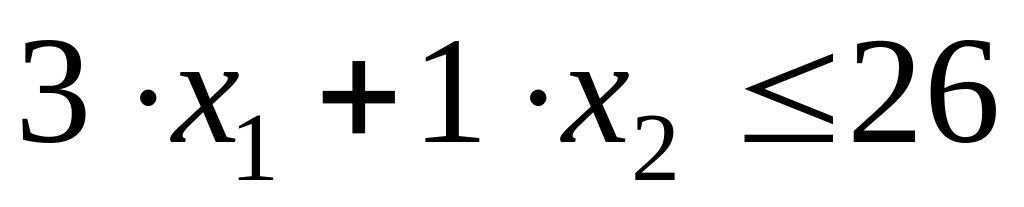или .

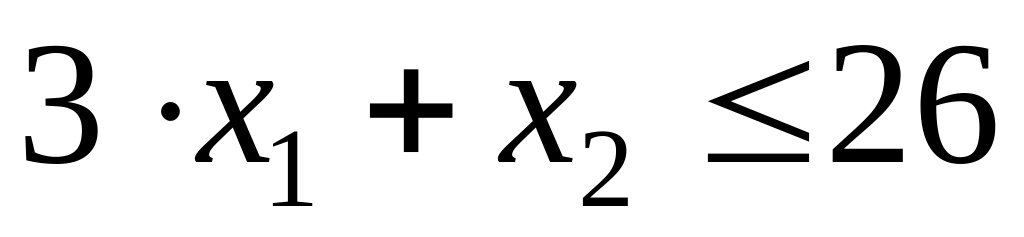Дополнительно на значения переменных накладываются ограничения неотрицательности и целочисленности.

Окончательно математическая модель задачи оптимизации будет иметь вид: