18. Расчет магнитного поля (интегральные выражения).

При решении прямых задач тело рассматривают как систему бесконечно большого числа диполей с упорядоченно расположенными осями магнитных моментов.

РИСУНОК 18.1. НАМАГНИЧЕННЫЙ ОБЪЕКТ И ТОЧКА ВЫЧИСЛЕНИЯ ПОЛЯ

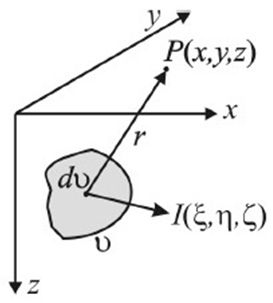
Пусть объем тела - v, а вектор намагничения - J. Тогда J*dv - магнитный момент элементарного объема dv. Магн. потенциал U для некоторой точки Р(х,у,z):

U(P) = 1/4*пи * интеграл по v (J*grad 1/r dv) (*), где вектор grad 1/r направлен по r в сторону его возрастания, 1/4*пи - коэффициент пропорциональности. Скалярное произведение J*grad 1/r можно представить в виде (в соответствии с правилами векторной алгебры): J*grad1/r = -div J/r + div J/r.

Тогда U(P) = 1/4*пи * (- интеграл по v div J/r dv + интеграл по v div J/r dv)

По теоремы Остроградского-Гаусса имеем: +интеграл по v div J/r dv = интеграл по S Jn/r dS , где Jn - проекция вектора намагничения на внешнюю нормаль n к поверхности S.

Таким образом, окончательно запишем:

U(P) = -1/4*пи интеграл по v div J/r dv + 1/4*пи интеграл по S Jn/r dS (**)

Для расчета м/поля можно использовать любое из урав.: (*) или (**)

При divJ = 0: U(P) = 1/4*пи интеграл по S Jn/r dS - формула справедлива только для однородно намагниченных тел.

19. Связь гравитационного и магнитного потенциала.

Пуассон установил, что в частном случае (намагнич. J и плотность sigma постоянны) гравитац. V и магн. U потенциалы количественно связаны м/у собой:

U = J/k*sigma * dV/di - формула связи потенциалов, где J/k*sigma - коэф. Пуассонна,

dV/di = (dV/dx * dx/di) + (dV/dy * dx/di) + (dV/dz * dz/di)

U= J * интеграл по тау (dтау/r^2 * cos тета) - магн. потенциал,

V= k*sigma*интеграл по тау dтау/r - гравитац. потенциал, где k=6.67*10^-8 см^3/г*с^2 - гравитац. постоянная.

Связь: Магнитный потенциал U однородно намагниченного тела с точностью до постоянного коэффициента равен производной гравитационного потенциала этого же тела, взятого по направлению намагниченности (теорема Пуассона).

СВЯЗЬ М/У ПРОИЗВОЛЬНЫМ И ВЕРТИКАЛЬНЫМ НАМАГНИЧЕНИЕМ

Za = Zв*sin(alfa)+Hв*cos(alfa)

Ha=Hв*sin(alfa)+Zв*cos(alfa)

Hв = На*sin(alfa)-Za*cos(alfa)

Zв = Za*sin(alfa)-Ha*cos(alfa)

20. Решение прямой задачи магниторазведки для тел простой формы.

ШАР

Вертикально намагниченный шар с центром на глубине h залегает под началом координат. Его потенциал: U = 4/3*пи*R^3*m*дэ/дэl (1/po), где m=J - магнитный момент единицы объема (намагниченность), 4/3*пи*R^3 = V - объем шара. M=V*J - магнитный момент шара.

Продифференцируем потенциал U по z и x. Совместим начало координат с проекцией центра шара. Начала координат поместим в точку наблюдения и получим выражения для составляющих Z (вертикальн.) и H (горизонт.):

Zа = M* (2*h^2-x^2 + у^2) / (x^2+h^2)^5/2

Hа = -M*3*h*x / (x^2+h^2)^5/2, где (x^2+h^2)^5/2 = ро^5.

ЦИЛИНДР

Геометрические аналоги цилиндра: линейные складки (антиклинальные, синклинальные), ровообразные впадины.

Выражения для Za и Ha полючают интегрированием по у выражений для шара.

Za = 2*M* (h^2-x^2)/ (h^2+x^2)^2,

Ha = -2*M* 2*h*x / (h^2+x^2)^2

ПЛАСТ МАЛОЙ МОЩНОСТИ

Тонкий пласт - пласт, у которого мощность во много раз меньше глубины залегания верхней кромки (2b << h). Выражения Za и Ha получают интегрированием от -бесконечность до +бесконечность по z выражений для цилиндра.

Za = 2*J*2*b *h/ (x^2+h^2),

Ha = - 2*J*2*b *x/ (x^2+h^2)

ПЛАСТ БОЛЬШОЙ МОЩНОСТИ

Для пласта большой мощности, безграничного на глубину и по простиранию, выражения Za и Ha получим из выражений Za и Ha для пласта малой мощности.

Заменим 2*b на dкси и х на х-кси, где кси - абсцисса середины верхней кромки пласта

Проинтегрируем выражения для тонкого пласта по кси в пределах его мощности и получим выражения:

Za = 2*J* (arctg (x+b)/h - arctg (x-b)/h).

Ha = -J*ln (h^2 + (x+b)^2)/(h^2 + (x-b)^2)