представить в виде полного дифференциала

, (21.32)

где Н= U + P V- энтальпия, или тепловая функция системы.

Изменение энтальпии в процессах, происходящих при постоянном давлении, равно количеству теплоты, подведенному к системе. Если теплообмен с окружающей средой отсутствует (dQ = 0), то ее энтальпия при изобарно-адиабатическом процессе постоянна (Н = const).

Отметим, что в области влажного состояния (см. рис. 21-1) давление паров жидкости не зависит от влажности материала и равно давлению насыщения паров свободной жидкости при температуре материала θ. Таким образом, при .

Будем считать, что температура жидкости . В зависимости от соотношения между температурами газа и жидкости, а также влагосодержания газа будут происходить изменения температуры жидкости и газа, а также испарение жидкости с поверхности. В условиях взаимодействия газа и жидкости процесс теплообмена осложняется переносом массы в виде пара жидкости, поэтому уравнение (21.32) примет вид

, (21.33)

где энтальпия жидкости; dW-изменение массы жидкости, отнесенное к единице массы сухой части газа.

Величина dW характеризует перенос влаги в виде пара с поверхности испарения в газовую фазу. При этом влагосодержание газовой фазы изменяется на бесконечно малую величину dx, т. е. , и дифференциальное уравнение (21.33) принимает следующий вид:

, или . (21.34)

После интегрирования уравнения (21.34) в пределах некоторых состояний 1 и 2 получим

. (21.35)

Независимо от направления процесса (испарение с поверхности или конденсация пара влаги на поверхности) между газом и жидкостью через определенное время установится динамическое равновесие. Здесь наблюдаются три физических явления одновременно: испарение жидкости, увеличивающее содержание влаги в газе, отбор из влажного газа теплоты, идущей на испарение жидкости, и повышение (понижение) температуры жидкости до значения, примерно постоянного на протяжении всего процесса насыщения газа. В состоянии полного насыщения температуры газа и жидкости становятся равными, что соответствует предельному равновесному состоянию. Эту температуру в изобарно-адиабатическом процессе называют температурой адиабатического насыщения газа. При некоторых условиях температура, показываемая смоченным термометром, соответствует температуре испаряющейся жидкости.

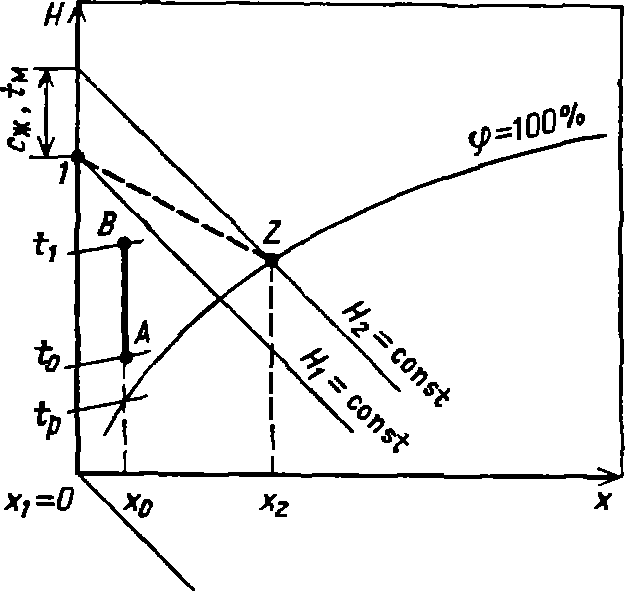
Рис. 21-4. К построению линий, отражающих изменение параметров влажного воздуха на диаграмме Н-х

Поэтому температура мокрого термометра t_м - это температура адиабатического насыщения газа.

Тогда

(21.36)

и

. (21.37)

Уравнение (21.37) соответствует прямой линии в координатах Н-х (см. рис. 21-4).

В случае исходного сухого воздуха точка 1, соответствующая начальному состоянию воздуха, имеет координаты

; Н₁, а конечному (точка 2)-х₂, Н₂. Пунктирная линия 1-2, описываемая уравнением (21.37), является линией постоянной температуры мокрого термометра.

При нагревании влажного воздуха в специальных теплообменниках-калориферах-его относительная влажность φ уменьшается, а влагосодержание х₀ остается постоянным. Поэтому на диаграмме Н-х процесс нагрева воздуха изображают отрезком АВ, проводя из точки, отвечающей начальному состоянию воздуха (t₀, х₀), вертикальную линию х₀ = const до пересечения с изотермой, отвечающей температуре нагрева воздуха t₁. Процесс охлаждения воздуха (имеющего начальную температуру t₁) при постоянном влагосодержании до его насыщения изображается вертикалью, проведенной из точки В вниз до пересечения с линией φ = 100%. При этом изотерма, проходящая через эту точку, определяет температуру точки росы t_p. Дальнейшее охлаждение воздуха, ниже температуры точки росы, приводит к конденсации из него части влаги и соответственно-к уменьшению его влагосодержания.

Отметим, что на диаграмме Н-х по двум независимым известным параметрам влажного воздуха можно найти точку, характеризующую его состояние, и определить все его остальные параметры. Для расчетов используют площадь диаграммы, расположенную над линией φ = 100% и отвечающую ненасыщенному влажному воздуху. Область диаграммы, находящаяся под линией φ = 100%, относится к воздуху, пересыщенному водяным паром, и для расчета процесса сушки интереса не представляет.

21.5. Материальный баланс конвективной сушки

Материальный баланс имеет целью определение количества (расхода) испаренной влаги и расхода сушильного агента. Его составляют для потоков высушиваемого материала и газа.

При составлении баланса по высушиваемому материалу в качестве исходных параметров используют влажность (w) и влагосодержание (w°) материала. Обозначив через G₁ и G₂ расходы исходного и высушенного материала, w₁ и w₂ - их влажности, а через W- расход удаляемой из материала влаги, получим материальный баланс в форме системы из двух уравнений:

, . (21.38)

Из системы (21.38) можно определить расход удаляемой влаги:

. (21.39)

Используя связь между влажностью материала w (массовые доли) и влагосодержанием:

,

получим уравнение для определения расхода удаляемой влаги:

. (21.40)

Эта влага в процессе сушки в виде паров поступает в сушильный агент, влагосодержание которого повышается. Таким образом, для газовой фазы можно записать следующее уравнение:

, (21.41)

где L- расход абсолютно сухого газа, кг/с; x₁, и х₂—влагосодержание газа соответственно на входе и на выходе из сушильной камеры в расчете на 1 кг абсолютно сухих газов, кг.

Из уравнения (21.41) найдем расход абсолютно сухого газа, необходимого для сушки:

. (21.42)

В расчетах и анализе процесса сушки используют понятие об удельном расходе абсолютно сухого газа l (в килограммах абсолютно сухого газа на 1 кг испаряемой воды):

(21.43)

21.6. Тепловой баланс сушки

По основному варианту конвективной сушки (рис. 21-5) сушильный агент, нагретый в калорифере, однократно проходит сушильную камеру, двигаясь прямо- или противоточно по отношению к материалу.

Обозначим параметры сушильного агента до калорифера индексом 0 (х₀, Н₀), после калорифера - индексом 1 ( x₁, Н₁ ) и после сушильной камеры индексом 2 (х₂, Н₂).

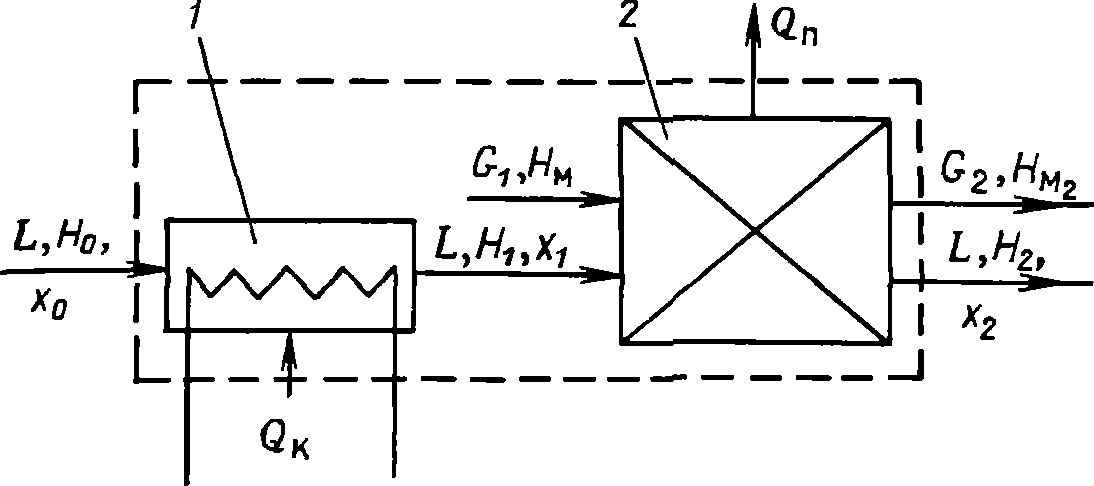
Рис. 21-5. К составлению теплового баланса конвективной сушилки:

1 - калорифер; 2 -сушильная камера

Влажный материал в количестве G₁, (в кг/с) при прохождении сушилки меняет свою энтальпию от Hм₁ до Hм₂. Считая энтальпию влажного материала аддитивно складывающейся из энтальпии высушенного материала и содержащейся в материале влаги, получим поток теплоты, входящий с материалом в сушилку:

, (21.44)

где с_м теплоемкость высушенного материала, Дж/(кг·К); θ₁,-температура материала, поступающего в сушилку, К, с_в - теплоемкость воды, Дж/(кг·К).

Поток теплоты с покидающим сушилку материалом

, (21.45)

где 02-температура высушенного материала, уходящего из сушильной камеры, °С.

Теплота, необходимая для сушки, подводится из калорифера (Q_к). Учитывая все поступающие (с сушильным агентом LH₀, с влажным материалом G₁H_M1) и уходящие (с сушильным агентом LH₂, С высушенным материалом G₂H_M2, потери теплоты в окружающее пространство Q_п) тепловые потоки, можно получить уравнение теплового баланса

(21.46)

Уравнение (21.46) может включать дополнительный член, учитывающий расход теплоты в дополнительном калорифере, иногда устанавливаемом в сушильной камере Q_доп. Кроме того, если в сушилке имеются перемещающие материал транспортные средства, которые покидают сушилку вместе с материалом, с ними входят (G_Tc_Tt_TH) и выходят (G_Tc_Tt_TH) тепловые потоки [здесь G_T - масса транспортных устройств, проходящих через сушильную камеру в единицу времени, кг/с; с_т - средняя теплоемкость материала, из которого выполнены транспортные устройства, Дж/(кг·К); t_т.н и t_т.к, - начальная и конечная температуры транспортных устройств, ⁰C].

В окончательном виде уравнение теплового баланса запишется

следующим образом:

. (21.47)

Общий расход теплоты на сушку

. (21.48)

Разделив обе части на расход удаляемой влаги W, получим выражение для удельного расхода теплоты (т. е. отнесенного к 1 кг испаряемой влаги):

, (21.49)

где q_м=(G₂/W)c_м( ) удельный расход теплоты на нагрев высушенного материала; q_т=(G_т/W)( ) - удельный расход теплоты на нагрев транспортных устройств; - удельные потери теплоты.

Удельный расход теплоты в основном (внешнем) калорифере можно также представить в виде

(21.50)

Подставляя значение q_к в выражение (21.49), находим

ИЛИ

. (21.51)

Обозначая правую часть уравнения (21.51) через Δ,

, (21.52)

получим следующее соотношение:

, или с учетом

(21.53)

Выражение (21.53), являющееся уравнением прямой линии, показывает, в какую сторону и насколько процесс изменения параметров газа в сушилке отклоняется от изоэнтальпийного. Это внутренний тепловой баланс сушилки.

Как уже указывалось, в отличие от конвективной контактная сушка реализуется путем передачи теплоты от теплоносителя к материалу через разделяющую их стенку. В качестве теплоносителя при контактной сушке обычно используют насыщенный водяной пар. При этом тепловой баланс непрерывно действующей контактной сушилки будет отличаться от соответствующего баланса конвективной сушилки.

Если к обозначениям, введенным ранее, принять, что расход греющего пара составляет D (в кг/с), его энтальпия Н_т.п (в Дж/кг), температура конденсации Т(в °С), теплоемкость конденсата греющего пара с_к [в Дж/(кг·К)], то тепловой баланс фаз контактной сушилки можно представить следующим выражением:

, (21.54)

или

. (21.54а)

Обычно уравнение (21.54а) решают относительно величины D с целью определения расхода греющего пара.