20.1.4 Кинетика адсорбции

Равновесная адсорбция. Кинетика равновесной адсорбции описы­вается уравнениями материального баланса (20.19) и изотермы (20.21). Поскольку скорость массопереноса принимается бесконеч­ной, в каждой точке аппарата фазы находятся в равновесии. Запишем эту систему, дополненную граничными условиями, прини­мая отсутствие продольного перемешивания (т. е. D_L = 0):

ε(дс/дх) + р_и,_с(дХ/дх) + w (дс/дх) = 0, (20.22) x=f(c), (20.23)

τ>0, х = 0, с = с₀, Х = Х₀, (20.24)

τ = 0, 0<х<х₀ с=φ(х) X =f (с*), (20.25)

τ = 0, х>х₀, с=0, X=0. (20.26)

Условия (20.24) - (20.26) означают, что в нулевой момент вре­мени (х = 0) на входе в слой адсорбента (л: = 0) находятся подвиж­ная фаза с концентрацией с = с₀ и равновесная с ней твердая фаза с концентрацией X = Х₀. Кроме того, они означают, что в адсор­бенте, имеющем остаточное содержание адсорбата, в начальный момент времени на участке 0<х<х₀ распределение адсорбиро­ванного вещества выражается функцией с=φ(х)

Условие (20.25) означает, что в начальный момент времени в слое на участке 0<х<х₀ есть какое-то остаточное содержание адсорбата.

Решение данной системы уравнений дозволяет найти скорость перемещения по слою точек, концентрация в которых постоянна. Для таких точек можно записать

дс = (дс/дх)dх + (дс/дτ)dτ = 0. (20.27)

Это равенство равнозначно следующему:

(дс/дх) (dx/dx) + дс/дх = 0. (20.28)

В связи с тем, что координаты х и τ связаны условием с = const, величина dx/dτ = U является скоростью перемещения по слою точки, имеющей концентрацию с.

Из уравнений (20.22), (20.23), (20.28) получим выражение для определения U:

U =w/ (ε +р_нас дХ/дс), (20.29)

где дХ/дс =f'(c) -производная функция изотермы в точке с концентрацией с.

Соотношение (20.29) позволяет проанализировать изменение профиля концентрации при его перемещении по слою. Отметим, что

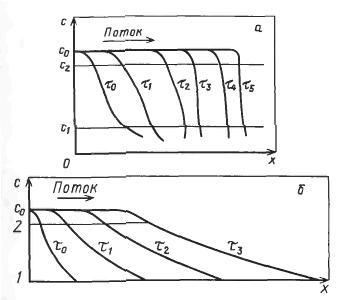
Рис. 20-4. Движение фронта сорбции по слою адсорбента при выпуклой (о) и вогну­той (б) изотермах

распределение концентраций в любой из фаз, достигнутое к неко­торому моменту времени, часто называют фронтом сорбции, или сорбционной волной, изменение которой во времени рассматривают как перемещение фронта сорбции.

В случае выпуклой изотермы (д²Х/дс² < 0), ввиду того что (дХ/дс)_С1 > (дХ/дс)_С2 при с₂> с₁, согласно уравнению (20.29) точки с большей концентрацией будут перемещаться по слою с большей скоростью, что приведет к постепенному сжатию начального про­филя (фронта сорбции) с=φ(х)до профиля (ступенчатого) беско­нечно малой толщины (рис. 20-4, а).

Если изотерма вогнутая (д²Х/дс²>0), ввиду того что (дХ/дс)_С1 < (дХ/дс)при с₂ < с₁, точки с меньшей концентрацией будут перемещаться с большими скоростями, что приведет к рас­ширению фронта сорбции (рис. 20-4,6).

В промышленных условиях скорость поглощения адсорбентом довольно высока, что часто делает условия процесса близкими к равновесных, поэтому данный анализ профиля концентраций при различных видах изотермы позволяет приближенно судить о влия­нии статических факторов на эффективность работы адсорберов. Из сделанного анализа видно, что при выпуклой изотерме условия сорбции наиболее благоприятны, так как «проскоковая», т. е. мини­мально допустимая, концентрация при ступенчатом профиле появ­ляется за слоем тогда, когда он полностью насыщен, что делает необходимую длину (или высоту) адсорбера минимальной.

В случае вогнутой изотермы условия наименее благоприятны, так как проскоковая концентрация может появиться за слоем

довольно быстро ввиду прогрессирующего расширения профиля концентраций.

Неравновесная адсорбция. Кинетика неравновесной изотерми­ческой адсорбции в отсутствие продольного перемешивания описы­вается системой уравнений (20.20) -(20.22). Возможность получения решения уравнений кинетики в аналитической форме и ввд этого решения зависят от вида функции, описывающей изотерму сорбции.

Ес. га форма изотермы выпуклая, задача кинетики на асимп­тотической стадии процесса имеет достаточно простое решение. В этом случае на форму перемещающегося фронта сорбции дейст­вуют два основных фактора: неравновесность сорбции, расши­ряющая фронт, и выпуклая форма изотермы, его сужающая. В ре­зультате конкурирующего действия этих двух факторов начиная с некоторого расстояния от входа потока по слою адсорбента станет перемещаться с постоянной скоростью фронт сорбции не­изменной формы (стационарный фронт).

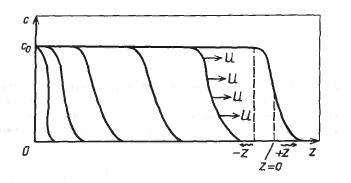
Замена текущего расстояния по длине слоя л: на расстояние по ширине профиля концентрации z (рис. 20-5) позволяет преобра­зовать уравнение (20.22) в частных производных в обыкновенное дифференциальное.

Выберем произвольную точку на пр( филе концентраций с или X. Если скорость перемещения начала координат равна U, а старой координатой произвольной точки с или X является л:, то значение новой координаты будет

z = х-Uτ. (20.30)

Концентрация в этой движущейся системе координат будет функцией только z, поскольку неизменный профиль перемещается вместе с новой системой координат.

Произведя замену переменных, получим следующую систему уравнений:

1/ ε (dc/dz)—Up_нас(dX/dz)+wdc/dz=0 (20.31)

-p_насU(dX/dz) =K_Vc[c-c^*(X)] (20.32)

Граничные условия:

τ→∞, z = -∞ , c= с₀, Х = Х₀, (20.33)

z =+∞, с=0, X= 0. (20.34)

Интегрирование уравнения (20.31) в граничных условиях (20.33) и (20.34) дает следующее выражение для скорости перемещения фронта:

и = wc/( ε + Р_нас X)=xс₀/( εс₀ + р_нас Х₀), (20.35)

откуда вытекает линейная зависимость между рабочими концентра­циями в подвижной фазе и адсорбенте:

с/с₀ = Х/Х₀ (20.36)

Поскольку в движущейся системе координат с=φ(z), z является функцией концентрации с:

Z=φ^-1c=z(c) (20.37)

где φ^-1 -функция, обратная φ.

В соответствии с соотношением (20.30) получим решение систе­мы уравнений кинетики в нелвном виде:

x=Uτ + z(c), (20.38) x=Uτ+z(X). (20.39)

Функции z(c) и z(X) получим интегрированием уравнения кине­тики (20.32) с учетом соотношений (20.35) и (20.36):

z(X)=- (20.40)

z(c)=- (20.41)

Константу интегрирования c₁ находят из материального ба­ланса:

c₁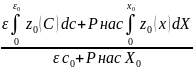₌ (20.42)

где z₀(X) и z₀(c)- первые слагаемые правых частей уравнений (20.40) и (20.41).

Уравнения (20.38)-(20.42) позволяют рассчитать профили кон­центраций в фазах, необходимую длину (высоту) слоя адсорбента при данном времени работы или, соответственно, время при за­данной длине слоя в случае выпуклой изотермы адсорбции при постоянной скорости движения фронта.

Следует отметить, что решения системы уравнений (20.38) и (20.39) совпадают по форме с уравнением Шилова, найденным им экспериментально:

τ=k₃L- τ₀ (20.43)

где к₃ -коэффициент защитного действия, с/м; L- длина (высота) слоя адсорбента, м; т₀-потеря времени защитного действия, с/м.

Сравнивая уравнения (20.38) и (20.43), найдем, что к,= 1/и и т₀ = z(c)/U. Решение системы уравнений кинетики изотермической адсорб­ции, верное не только для стационарного фронта, движущегося с постоянной скоростью, в аналитической форме известно лишь для случая линейной изотермы. Однако несмотря на то что это решение справедливо лишь для линейной изотермы, его с помощью соот­ветствующих поправок используют и для нелинейных равновесных зависимостей, объединенных следующим уравнением:

Х*/Х*(с₀) = (с/с₀)/[с/с₀ + r(1 - с/с₀)], (20.44)

где г- постоянная величина, называемая фактором разделения.

В случае ленгмюровской изотермы фактор разделения опреде­ляется по формуле

r = 1/(1 + кс₀). (20.45)

Для линейной изотермы r= 1.

Решение системы уравнений кинетики при постоянном факторе разделения выглядит так:

а) адсорбция, исходный адсорбент-чистый (Х_н = 0):

(20.46)

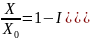
где n_0c=K’v_c-общее число единиц переноса для слоя сорбента длиной х, Т= wс₀[τ — хс)/w] Р_нас X^*(C₀) х - безразмерное время:

K’_Vc=2 K’_Vc/(r+1) при 0,2<r<1

K’_Vc= K’_Vc/(r+1) при r>1

K’_Vc= K_Vc при r=1

пересчет объемного коэффициента массопередачи К_Ус в К'у_с необходим для корректировки уравнений (20.46) и (20.47) в случае, когда г ф 1, полностью верных только для линейной изотермы (г = I); функция /(а, Р) представляет собой ряд сходящийся при достаточно больших значениях а и р. Величины функции I обычно представляют в табличной форме в зависимости от параметров а и Р;

б) изотермическая десорбция, уравнения (20.44)-(20.47) видоизменяются:

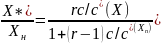(20.48) r=1+kc*(X_n ) (20.49)

(20.50)

(20.51)

Уравнения (20.44)-(20.51) служат для расчета профилей концентраций и опре­деления времени процесса или длины слоя сорбента при изотермической адсорбции Десорбции), изотерма которой подчиняется обобщенным уравнениям (20.44), (20.48).