22.3. Экстрагирование твердого вещества

Твердые пористые частицы содержат целевой компонент в твердом виде. Возможны различные варианты распределения целевого ком­понента по объему частицы. Во многих случаях реализуется равно­мерное распределение извлекаемого вещества по объему пористого тела. В процессе экстрагирования область, заключающая в себе извлекаемое вещество, систематически уменьшается в объеме (рис. 22-4). Область, освобожденная от твердого извлекаемого ве­щества, содержит это вещество в растворенном виде. С течением времени объем этой области возрастает.

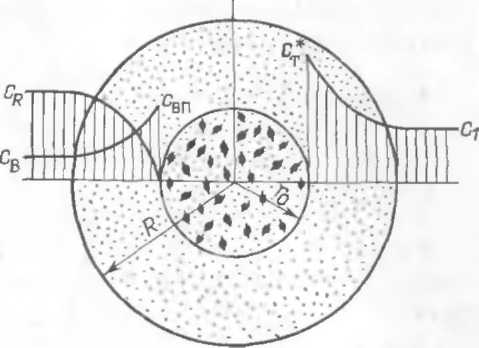
Рис. 22-5. Изменение концентраци­онных полей в процессе экстрагиро­вания твердого вещества

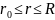В правой части рис. 22-5 изображено распределение концентрации при простом физическом растворении вещества в экстрагенте, в левой его части-распреде­ление концентраций реагента и продуктов реакции ( и с_в) при химическом растворении. Перейдем к математическому описанию массообмена при экстрагировании твердого вещества, физически растворимого в экстрагенте. Концентрационное поле в области описывается дифференциальным уравнением диффузии (22.10)

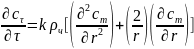
и краевыми условиями

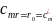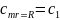; (22-17)

Если допустить, что все извлекаемое вещество сосредоточено в сфере радиуса 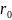, а плотность его распределения (масса извле­каемого вещества в единице объема частицы) 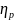= 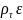, то изменение массосодержания происходит вследствие диффузии вещества с по­верхности сферы радиусом R в основную массу жидкости:

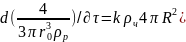. (22.18)

Это уравнение определяет границы области 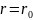заключаю­щей в себе вещество в твердом состоянии, в каждый момент времени т. Имеется возможность еще более упростить рассматри­ваемую систему уравнений (22.10), (22.17), (22.18). Для этого следует обратить внимание на то, что экстрагирование твердого вещества-процесс медленный, и поэтому в каждый момент времени в области «успевает» установиться стационарное распределение концентраций, удовлетворяющее уравнению

.

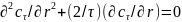Решение этого уравнения в граничных условиях (22.17) имеет вид

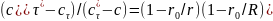(22.19)

Подстановка (22.19) в (22.18) и решение полученного при этом дифференциального уравнения приводит к окончательному резуль­тату:

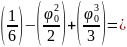, (22.20)

Где

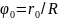
Время полного экстрагирования твердого вещества определит­ся из (22.20) при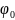 = 0:

. (22.20а)

В заключение укажем на возможность решения более общей задачи прямоточного и противоточного экстрагирования. Для это­го вместо допущения = const следует использовать уравнения материального баланса, как это сделано при рассмотрении преды­дущих тем.

Теоретическое описание кинетики растворения или экстрагиро­вания в сочетании с экспериментом может служить основой для инженерного расчета. Другим способом расчета является опреде­ление числа теоретических ступеней равновесия, как это делается при расчете жидкостной экстракции. Введение коэффициента по­лезного действия, учитывающего степень приближения к равнове­сию, позволяет определить число необходимых ступеней равнове­сия. Ясно, что этот коэффициент полезного действия также опре­деляется временем контакта фаз, т. е. той же кинетикой растворения или экстрагирования.