27. Корреляционная функция и спектральная плотность стационарных случайных процессов.

Корреляц. ф-ция стационар. СП r_x(t,) – детерменир. ф-ция времени двух переменных: времени t и сдвига по времени , значение кот. для каждой пары переменных t и  равно корреляц. моменту двух сечений СП при t и t+. r_x(t,) определ. вероятностную взаимосвязь двух сечений СП. Оценка:

(t,)=1/n∙(t)∙(t+).

К определению r_x(t,)

Стационарный случ. процесс: r_x(t,)= r_x(). Характерный график r_xx() стационар. СП.

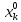(t)∙(t+)

Эргодические стационарные СП–СП для которых вероятностные хар-ки, определенные по множеству реализаций, совпадают с вероятностными хар-ками, найденными усреднением по времени реализации.

Для эргодич. СП r_xx()=1/T∙dt.

Св-во корреляц. ф-ции эргодич. случ. процесса:

r_xx(t)=r_xx(–t) – четно симметричная убыв-ая ф-ия корреляц. сдвига .

Схема расчета r_xx(t)

Св-ва r_xx(t):

1) Четно симметричная, убыв. ф-ция корреляц. сдвига

 { r_xx(t)=r_xx(–t); r_xx(t)<r_xx(0)};

2) r_xx(0)=D_x=_x² есть дисперсия СП.

Корреляц. функция вых сигнала

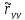()=1/T∙(t)∙y⁰(t+)dt=1/T∙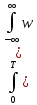(ξ)x⁰(t–ξ)dξ]∙[(η)x⁰(t+–η)dη]dt

После смены порядка интегрирования:

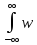()=(ξ){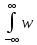(η)∙[1/T∙(t–ξ)∙x⁰(t+–η)dt]dη} dξ

Заметим:

1/T∙(t–ξ)∙x⁰(t+–η)dt=(+ξ–η).

Итак, корреляц. ф-ция вых. Сигнала

()=(ξ)∙(η)∙(+ξ–η)dη dξ.

Спектральная плотность мощности стационарного СП

G_xx()=_xx­()∙e^{–i∙∙}d — преобраз. Фурье r_xx(t).

Физический смысл–предел дисперсии СП, приход. на интервал + к значению этого интервала

G_xx()=_xx­()∙e^{–i∙∙}d=G_xx(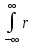)=_xx­()∙cos()d–i∙_xx­()∙sin()d, где _xx­()∙sin()d=0, т.к. ф-ция нечетная.

В силу четности r_xx(t)спектральная плотность –веществ. неотриц ф-ция частоты Типичная форма G_xx()

Выполнив обратное преобразов. Фурье G_xx() получим r_xx()=1/(2∙π)_xx­()∙e^{i∙∙}d;

D_x=r_xx(0)= 1/(2∙π)_xx­()d

Определение спектральной плотности вых. Сигнала

G_yy(s)=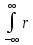_yy­()∙e ^–s∙d.

После подстановки () в G_yy(s), получим

G_yy(s)=^–s∙d(ξ)dξ∙(η)∙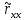(+ξ–η)dη.

Представим e^–s∙= e^{–s∙(+ξ–η)}∙e^s∙ξ∙e^–s∙η.

При этом

G_yy(s)=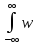(ξ)∙e^sξdξ∙(η)∙e^–s∙ηdη∙(+ξ–η)∙e^{–s∙(+ξ–η)}d(+ξ–η).

Здесь:

1) (ξ)∙e^sξdξ=W(–s);

2)(η)∙e^–s∙ηdη=W(s); 3)(+ξ–η)∙e^{–s∙(+ξ–η)}d(+ξ–η)=G_xx(s). Таким образом G_yy(s)=W(–s)∙W(–s)∙G_xx(s).

28. Взаимная корреляционная функция и взаимная спектральная плотность входа и выхода линейной динамической системы. Взаимная корреляционная ф-ция СП x(t) и y(t).r_xy()=

Взаимная корреляционная ф-ция определяет вероятностную взаимосвязь двух случайных процессоы.

Геометрич. смысл. Св-ва взаимн.корреляционной ф-ции.Заменим переменную .Тогдаr_xy()=.Взаимная корреляционная ф-ция СПx(t) и y(t) не явл. четно семмитричной и обладает след. св-вом: r_xy()=r_yх().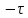

Максимум r_xy() достигается при>0 (макс. коррел. ф-ции при).Типичный видr_xy()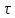

Взаимная корреляц. ф-ция вх. и вых. СП. Подставив в ф-лу ВКФ интеграл свертки, получим: ř_xy()=. Рассмотрим случай, когда на вых. сигнал наложена помеха,независимая от вх. возд.m_y=h_уст·m_x+m_n; r_yy()=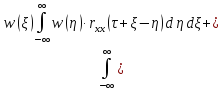r_nn(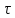).r_xy(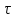)=. Использование преобразования Фурье позволяет упростить определение взаимн. кор. ф-ции СП на вх. в лин. динамич. сис-му и выходе из нее. Применив к (1) это преобразование, получим:G_xy(iω)=W(iω)·G_xx(iω); где G_xy(iω)=.Фурье-изображение взаимной корреляционной ф-ции 2 случ. процессов – взаимная спектральная плотность мощности 2 случ. процессов.G^-_xy(s) и G⁺_xy(s) для G_xy(s) не равны друг другу. Взаимн. спектр. пл-ть явл. комплексной ф-цией частоты. Если поменять знак: G_xy(iω)=, тоG_xy(iω)= G_yх(-iω).