23. Частотный показатель колеб-ти. Запас устойчивости по максимуму ачх замкнутой системы. М-окружности и их свойства

Запас устойчивости системы м оцениваться по виду импульсной переходной характеристики её замкнутого контура. Такая оценка обладает наглядностью, что оказывается важным при расчёте сложных структур САУ, в также при расчёте схем с цифровыми контроллерами.

Колебательному характеру переходной, а следовательно, и импульсной переходной характеристике соответствует появление в графике модуля КЧХ (гр-к АЧХ) резонансного пика. То же самое справедливо и для контуров произвольно высокого порядка, в том числе и контуров с запаздыванием. Высота резонансного пика зависит от степени приближения КЧХ разомкнутого контура к «опасной» точке -1, j0 (по кр Найквиста охват этой точки указанной КЧХ приводит к неустойчивости замкнутого контура).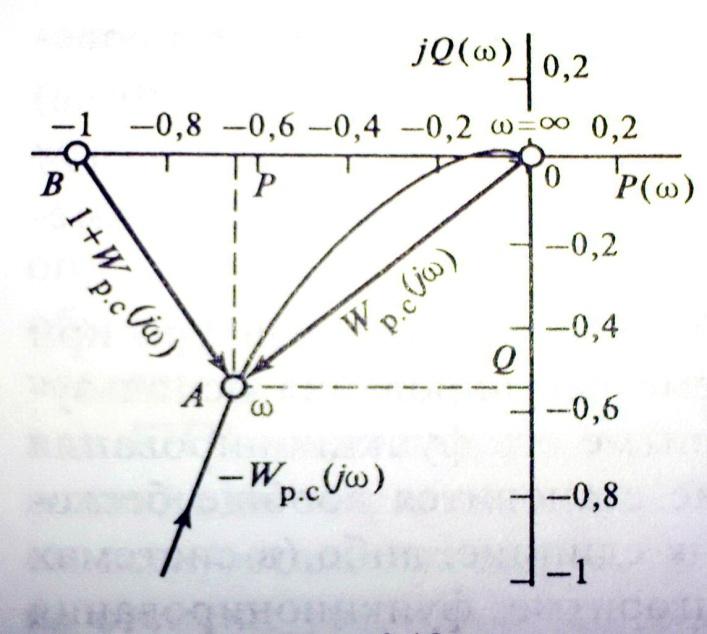

Модуль КЧХ: |Ф(jw) | = | W_pc(jw) |/|1 + W_pc(jw) |

Допустим, что х-ка р.к. W_pc(jw) располагается в компл-й плоскости как показано на рисунке.

Числитель для нек-й фиксированной частоты ω равен длине вектора W_рс(jw), т.е. отрезку ОА, а знаменатель – длине вектора, проведённого к W_рс(jw) из точки -1,j0, т.е. отрезку ВА. Поэтому знач. модуля Ф(jw) в графической интерпретации представляет собой отношение длин отрезков ОА и ВА: |Ф(jw) | = ОА/ВА. Проследим, как меняется это отношение при изм-ии частоты от ω=0 до ω=.

Обычно в сист рег-ия значение КЧХ р.к. при нулевой частоте достаточно велико; если же в сист регулирования используется рег-р с интегральной составляющей в алг его функционирования (И-, ПИ-, ПИД-), её значение становится вообще бесконечно большим. Поэтому значение Ф(j0) вообще близко к единице, либо (в сист регулирования с интегральной составляющей) равно единице. С ростом частоты т.А движется по направлению стрелки и в пределе, при ω -> длина вектора ОА стремится к нулю, а вектора ВА – к единице; соответственно модуль характеристики также стремится к нулю. Однако характер изменения отношения векторов при промежуточных значениях частоты 0 <ω < оказывается различным в зав-ти от удаления х-киW_рс(jw) от точки -1,j0 (точка B).

Если характеристика W_рс(jw) располагается достаточно далеко от точки -1,j0,длина вектора ВА при указанном перемещении точки А всё время остаётся больше длины вектора ОА и их отношение монотонно уменьшается от значения |Ф(jw)| при ω=0 до нуля при при ω -> . Если же х-каW_рс(jw) располагается близко к точке 1, j0, то вначале отношение отрезков с ростом частоты возрастает, поскольку длина вектора ОА уменьшатся медленнее, чем происходит уменьшение вектора ВА. Достигнув максимального значения при некоторой частоте ω_рез, это отношение затем устремляется к нулю.

24. . Прямые и косвенные критерии качества процессов регулирования.

Прямые: динамическая ошибка, время регулирования, степень затухания.

Для оценки динамич. точ-ти АСР исп-т прямые пок-ли кач-ва и косвенные-интегральные критерии кач-ва.

Линейный интегральный критерий и его свойства.I₁=. В АСР с И-,ПИ-,ПИД-рег-ми значениеI₁ опред-ся значением коэф-та при интегральной составляющей I₁=1/k_и.Минимуму I₁ отвечает максим. допустимое значение k_и.

Св-ва:

1.Связан простым соотношением с парам-ми настройки рег-ов

2.Инвариантен по отношению к точке приложения возмущения.

3.Без ограничения на запас уст-ти прим-ся не может.

Квадратичный интегральный критерий и его свойства. I₂=.

Св-ва:

1.не инвариантен по отношению к точке приложения возмущения.

2.Вычисления произв-ся по модулю КЧХ сис-мы.

3. Может применяться без ограничения на запас уст-ти.

Модульный: I=

Выбор оптимальных настроек П-, И-, ПИ-, ПИД-алгоритмов.

При выборе настроек высший приоритет-запасу уст-ти.

Порядок расчета оптим. настроек при ограничении m=m_доп­:

1.расчет линий заданного запаса уст-ти m=const.

2.Выбор критерия(показ-ля)кач-ва.

3.Определение оптимальных настроек.

4.Расчет переходного процесса и определение прямых показ-лей кач-ва.

При настройках,соотв. точке (k_и)_max при α_крит.:

1.Достиг-ся максим. кач-во АСР по лин. интегральному критерию k_и=[(k_и)_max]_max2.Характеристич. ур-ие замкнутой АСР имеет пару сопряженных комплексных корней кратности 2, нарушается соответсвие м/у показ-ми запаса уст-ти m,M и ψ.4. АСР стан-ся чувствительной к вариациям пар-ов рег-ра.

k_п(m,ω)=;k_и(m,ω)=.