41. Метод фазовых траекторий

Метод анализа устойчивости состояния равновесия и автоколебаний автономной системы.

Изучение состояния системы отображается на фазовой плоскости движения изображающей точки. След от движения изображающей точки называется фазовой траекторией.

Координата изображающей точки по оси абсцисс определяется значением выходной переменной y в момент времени t, по оси ординат - значением первой производной по времени dy/dt в этот же момент времени. Стрелками показывают перемещение изображающее точки в течение времени.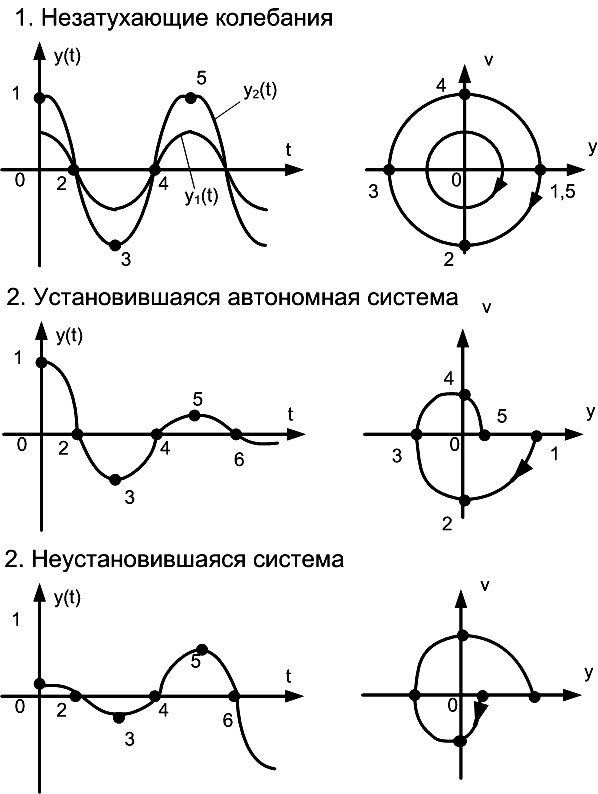

Полную совокупность различных фазовых траекторий называют фазовым портретом. Он задаёт представление о всех возможных движениях системы в зависимости от н.у.

Чтобы определить устойчива ли система необходимо выявить качественную картину фазовых траекторий.

Метод изоклин. Уравнение системы второго порядка можно получить из уравнения состояния

Полученное уравнение ставит в соответствие каждой точке плоскости z₁,z₂ определённое значение dz₁/dz₂.

Геометрическое место точек dz₁/dz₂ = const в плоскости z₁,z₂ определяется уравнением: f_1,0 (z₁(t), z₂(t)) – C f_2,0(z₁(t), z₂(t)) = 0.

Линия в плоскости z₁,z₂, кот определяется этим уравнением называется изоклиной.

Изоклина - геометрическое место точек с одним и тем же наклоном касательной к фазовой траектории (угол наклона касательной отмечают на изоклине чертой со стрелкой).

Семейство изоклин позволяет построить для заданных н.у. в плоскости переменных состояния фазовых траекторий.

Уравнения состояния ОУ:

Уравнения регулятора Δx₁ = -k_pΔz₂

Для уравнения изоклин следует задать значения всех коэффициентов в уравнениях состояния и значения k_p

По условию примера:

В общем случае нелинейное ДУ 2-го порядка имеет вид:

42. Прямой метод исследования устойчивости а.М. Ляпунова.

Сущ-т 2 метода исследования уст-ти Ляпунова:

1-ый:основан на решении сис-мы нелин. диф. ур-ий.

2-ой: основан на использовании критериальной формы и не сопряжен с непосредств. решением диф. ур-ий.

Прямой метод-метод изучения уст-ти движения,заключ. в отыскании ф-ций V=f(t,y₁,..,y_n), и их полных производных по времени,св-ва которых позв-т судить об уст. нелин. сис-мы.

Диф.нелин. ур-ия возмущенного движения:

Определяющим сост. равновесия,кот. м.б. устойчивым и неуст.Вводимая спец. ф-ция переменных состояния V(y₁,..,y_n) обл-т св-ми:1.V(y₁,..,y_n) непрерывна и имеет непр. частные производные.2.V(0,..,0)=0.3.V(y₁,..,y_n)>0 за исключ. т. y_i=0.Ф-ция ляпунова,удовл. этим св-вам наз. знакоопределенной положительной ф-цией.Если V принимает нулевые знач. не только в начале координат,а в остальных точках пр-ва сохраняет постоянный знак она наз. знакопостоянной.

Для решения вопроса об сут-ти невозмущенного движения Ляпунов докаказал 2 фундаментальные теоремы.

1 теорема:Если диф. ур-ия автономной сис-мы таковы,что возможно найти знакоопределенную положительную ф-цию V(y₁,..,y_n), полная производная которой в силу ур-ий есть ф-ция знакопостоянная отриц,то равновесие в нач. координат устойчиво.

2 теорема:Если диф. ур-ия автономной сис-мы таковы,что возможно найти знакоопределенную положительную ф-цию V(y₁,..,y_n), полная производная которой в силу ур-ий есть ф-ция знакоопределенная отриц,то сост. равновесия в нач. координат асимптотически устойчиво. Определение полной производной ф-ции Ляпунова не требует решения сис-мы диф. ур-й

Частный пример ф-ции Ляпунова квадратичная форма V=a₁·y₁²+a₂·y₂²+a₃·y₃²,a_i>0. Ф-ции V=a₁·y₁²+a₂·y₂²+a₃·y₃² в пр-ве переменных сост. y_i отвечают односвязные пов-ти V=a₁·y₁²+a₂·y₂²+a₃·y₃²=с_k,окружающие начало координат,а опред. набору y_i-точка М_к на пов-ти с_к.Мн-во М_к образуют фазовую траекторию.Если dV/dt<0, то с ↑ t изображающая точка будет перемещаться с пов-ти с большим знач. с на пов-ть с меньшим с,т.к знакоопределенная положит. ф-ция может только ↓, если dV/dt<0:фазовая траектория 1 на рисунке.

Условие dV/dt<0 не явл. необх. усл. уст-ти.Сост. равновесия м.б. уст. и при траектории 2.

Теория Ляпунова дает только достаточные усл. уст-ти сост. рановесия нелин. сис-мы.