36. Дискретные системы, их виды. Цифровая реализация типовых алгоритмов регулирования.

Виды дискретных сигналов и систем.различ. два вида изменяющ. во времени величин:

1)непрерывные, определяемые в любой момент времени(темп-ра, напряж. и т.п.);

2) дискретные, принимающ. отличные от нуля знач. только в некотор. определенные моменты времени. В сист. управл. непрерыв. технологич. процессами переходят к дискретным сигналам с целью расшир. ф-цион. возможностей управляющ. и/или измерит. устройств. Непрерывные сигналы преобраз. в импульс. или числов. последовательности.

Сист. назыв. дискретной, если в цепи преобразов. сигналов хотя бы один из сигналов явл. дискретным. Дискрет. сист. приобретает особые не присущие непрерыв. сист. св-ва и должна исследов. методами спец. теории дискрет. сист. Современная сист. управл. технолог. процессами содержит непрерыв. элементы, элем. с непрерыв. вх. и дискрет. вых. и элем. с дискрет. вх. и дискрет. вых.

Дискрет. сист.:

1) импульсные а)с амплитуд-импульс. модуляцией, б)с широтно-импульс. модуляц., в)с частотно-импульс. модул., г)дельта импульс.]; 2) цифровые.

Цифровая реализация типовых линейных алгоритмов регулирования

П-алгоритм. Передаточная функция

W_ву(z) = k_p W_дш(s) =

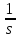
W(z) = W_ВУ(z)W_ДШ(z) = k_p = k_p(1 – z^-1)

W(s) = k_p(1 – e^-Ts)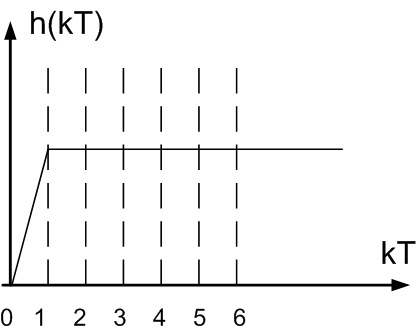

W_pэ(s) = W_ДШ(s)W(s) = (1 – e^-Ts)

Переходная характеристика:

h_p(t) = (k_p/T) [t – (Ф – 1)(t – T)]

И-алгоритм. Передаточная функция

W_ву(z) =

W(z) = W_ВУ(z)W_ДШ(z) =

W(s) = k_иT

W_pэ(s) = W(s) =k_иT =

ПИ-алгоритм. Передаточная функция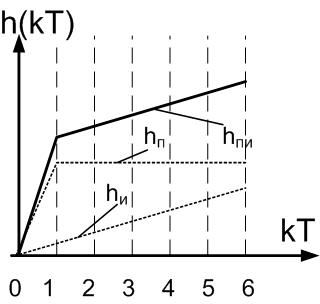

W_pэ(s) = (1 –e^-Ts) +

W_pэ(s) = (1 – e^-Ts + )

Переходная характеристика:

h_p(t) = k_p [t – (Ф – 1)(t 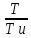– T) + t]

Идеальный Д-алгоритм

ПИД-алгоритм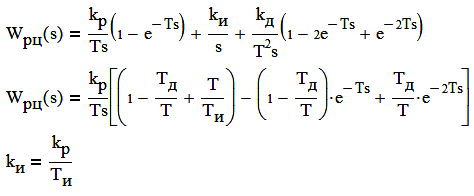

37. Математическое описание дискретных систем. Дискретное преобразование Лапласа и z-преобразование.

Дискрет. преобразов. Лапаса и Z-преобразов.

Дельта-имп. послед. может быть представл. в виде:

x*(t)=(t)∙(t–k∙T)=x[kT]∙(t–k∙T).

X(s)=(t)∙e^–s∙dt; X*(s)=[kT](t–k∙T)∙e^–s∙dt.

Таким образом X*(s)=[kT] e^–kTs.

Формула Z-преобразов.:X(z)=[kT] z^–k, где z=e^sT.

Математическое описание дискретных систем.

СПИП–сист. преобразов. имп. последоват.. Неравновес. режимы имп. сист. описыв. ур-ниями

y*(t)+C₁∙y*(t–T)+…+C_r∙y*(t–r∙T)=d₀x*(t)+d₁∙x*(t–T)+…+d_l∙x*(t–l∙T).

При t=kT эквивал. форма описания дискрет. сист.:

y[kT]+C₁∙y((k–1)T)+…+C_r∙y*((k–r)∙T)=d₀x[kT]+d₁∙x((k–1)T)+…+d_l∙x((k–l)∙T). Решение для любой заданной числов. последоват. x[kT] находится: y[kT]=d₀x[kT]+d₁∙x((k–1)T)+…+d_l∙x((k–l)∙T)–C₁∙y((k–1)T)–…–C_r∙y*((k–r)∙T). Разностные ур-ние получается из дифференциального при замене дифференциалов приращениями dxx;dyy. при малых T:

1) dxx=x[kT]–x[(k–1)T]; dx/dt;

2)d²x²x=x[kT]–x[(k–1)T];

d²x/dt² = =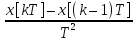

= .

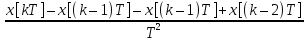38. Передаточная функция дискретной системы.

В рез-те z-преобразования разностного ур-ия:y[kT]+c₁·y[(k-l)·T]+..+c_r·y[(k-r)·T]=d₀·x[kT]+d₁·x[(k-1)·T]+..+d_l·x[(k-1)·T] получим(1+с₁·z^-1+с₂·z^-2+..+с_r·z^-r)·Y(z)=(d₀+d₁·z^-1+d₂·z^-2+..+d_l·z^-l)·X(z).Передаточная ф-ция дискретной сис-мы-отношение Y(z) к Х(z):W(z)=Y(z)/X(z)=(d₀+d₁·z^-1+d₂·z^-2+..+d_l·z^-l)/(1+с₁·z^-1+с₂·z^-2+..+с_r·z^-r).После умножения числителя и знаменателя на z в положительной степени (n=r) получаем:W(z)=Y(z)/X(z)=.Определение хар-к дискретной сис-мы в обл-ти изображений производ-ся по таким же правилам,что и систем непрерывных.При последовательном соединенииn эл-ов W_с(z)=W₁(z)·W₂(z)·..· W_n(z).При параллельном соединении W_c(z)=.При встречно-параллельном соединении:W_з.с.(z)=.

Передаточные ф-ции дискретных звеньев.

Апериодическое звено:Т_a·+y(t)=k_а·x(t);Т_a·+y[kT]=k_а·x[kT];·y[(k+1)·T]+(1-)·y[kT]=k_а·x[kT];·Y(z)=k_a·X(z);W(z)=Y(z)/X(z)=.

Интегрирующее звено:y(t)=k_и·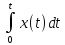→=k_и·х(t);y[kT]-y[(k-1)·T]=kи·T·x[kT];(1-z^-1)·Y(z)=kи·T·X(z);W(z)=Y(z)/X(z)=.

Дифференциирующее звено:y(t)=k_д·→y[kT]=·( x[kT]- x[(k-1)T]);Y(z)=·(1-z^-1)·X(z);W(z)=Y(z)/X(z)=·(1-z^-1).