2. Понятие математической модели. Методы математического описания оу. Дифф. Ур-ия дин. Систем, методы решения, линеаризация

Математич. модели ОУ:

1) расчетные на основе физич. з-нов (дифференц. уравнения);

2) основанные на экспериментальных динамич. хар-ках.

Расчетные сложно сделать. По переход. хар-ке перейти к передаточн. ф-ции математически некорректно.

ДХ-динаимч. хар-ка. Критерии адекватности – минимум отклонения аппроксимирующей хар-ки от экспериментальной: в среднем – минимум среднего квадратичного отклонения; в определенных характерных точках.

Пример получения модели:

аппроксимируем кривую разгона (не переходную характерист.) для объектов с самовыравниванием (одноемкостные, двухемкостные, многоемкостные) с помощью произведения нескольких А-звеньев и звена запаздывания. Для вычисления коэф. моедли использ.:

1) значения k–коэф. передачи модели, τ₀–время запаздыв., T₀–постоянная времени объекта;

2) координаты точки перегиба t_п, h_п(t_п);

3) значение производных h_п’(t_п) и h_п”(t_п) в точке перегиба.

Для построения модели использ. критерии приближения:

1) h_а(0)=h_э(0);

2) h_а(∞)=h_э(∞);

3) h_а’(t_п)=h_э’(t_п);

4) h_а”(t_п)=h_э”(t_п).

Модель объекта удовлетворяет требованиям точности, если после подачи одних и тех же входных воздействий на систему управления с реальным объектом и систему с его моделью при оптимальном алгоритме функционирования контроллера разность выходных величин обеих систем окажется достаточно малой. Математич. модель предполагается заранее известной и может быть использована для определения алгоритма ф-циониров. контроллера (алгоритм управл.) При построении модели объекта и контроллера следует, когда это возможно, стремиться к составлению линейных математических моделей.

Имитационная математич. модель: y_э – экспериментальное значение; y_р – реакция; e – точность (ошибка).

Дифференциальные уравнения динамических систем, их решение. В ТАУ представляют ЛДУ: _·+_·+..+Т₁·+y(t)= k·x(t).

Методы решений ЛДУ:

1.Классические методы теории ЛДУ;

2. Операционный метод;

3.Символьное и численное решение с использованием математических пакетов(Mathcad,Matlab).

Классич. метод: решение ЛДУ ·+..+ Т₁· +y(t)=f(t) имеет вид y(t)=y_св(t)+ y_вын(t), где y_св(t)-общее решение однородного ДУ; y_вын(t)-частное решение. Общее решение имеет вид: y_св(t)=С₁·+ С₂·+ С_n·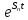,гдеS_k-корни ур-ия: _·Sⁿ+_·S^n-1+..+T₁·S+1=0.

Преобразование Лапласа. Х(s)=,гдеX(s)-изображение x(t), x(t)-ф-ция-оригинал; s=-αjω; X(s)=L{x(t)}.

Понятие передаточной функции.

Передаточная ф-ция линейной системы W(s): W(s)=Передаточная ф-ция - хар-ка, представляющ. собой преобразование Лапласа импульсной хар-ки системы;отношение преобразованных по Лапласу при нулевых н.у. выхода ко входу:W(s)=Y(s)/X(s).X(s)-вх.воздействие. Переход к оригиналу- по ф-ле обратного преобразование Лапаласа:x(t)=,t>0,c=Re(s).

Порядок решения ДУ операторным методом:

1.Преобразовать ДУ по Лапласу.

2.Для заданного оригинала x(t) определить изображение входа Х(s).

3.Записать выражение для выходной величины Y(s)=B(s)/A(s).

4. Определить оригинал y(t). В общем случае:B(s)=b_m·S^m+ b_m-1·S^m-1+..+b₁S+b₀; А(s)=a_n·Sⁿ+ a_n-1·S^n-1+..+a₁S+a₀. Y(s) следует представить суммой простых дробей:Y(s)=S_k-корни ур-ия, C_k-коэф-ты. Действительному корню S_k=α кратности r соответствует rпростых дробей вида: .