5.4. Цена победы

При данном подходе оценка трудозатрат производится таким образом, чтобы она была самой выгодной для заказчика и контракт был бы гарантированно заключен. Т.о. оценка основывается на бюджете заказчика а не на конечной функциональности ПО. Например, если разумная оценка для проекта составляет 100 человеко-месяцев, но заказчик может оплатить только 60 человеко-месяцев, то оценщика просят изменить оценку, до 60-ти человеко-месяцев, чтобы выиграть проект. Это также очень плохой подход, который однако очень часто встречается на практике вследствие "политических игр руководства", и он с очень высокой степенью вероятности, вызовет задержку поставки или вынудит команду работать в сверхурочное время.

6. Алгоритмические методы

Используемый в алгоритмических моделях математический аппарат весьма разнообразен и варьируется от простых линейный формул, использующих математическое ожидание и среднеквадратичное отклонение, до сложных регрессионных моделей [12] и дифференциальных уравнений [11]. Как правило, чтобы улучшить точность алгоритмических моделей, их требуется приспособить (например, с помощью пересчета основных параметров и коэффициентов) к конкретным обстоятельствам. Причем, даже после такой калибровки точность может оставлять желать лучшего. Поэтому, можно считать, что у каждой конкретной модели есть своя конкретная область применения, в которой она может дать адекватный конечный результат.

Все алгоритмические методы основаны на математических моделях которые определяют трудозатраты как функцию зависящую от множества переменных соответствующих основным влияющим на трудозатраты факторам и имеют общий вид:

(7)

Здесь E - суммарный объем трудозатрат (например, в человеко-часах), а x_i, i = 1,...,n - учитывающиеся факторы. Соответственно многообразие алгоритмических методов обуславливается двумя основными аспектами: выбором факторов и формой функции f. В зависимости от этого, среди алгоритмических моделей могут быть выделены 3 основных группы:

• Линейные модели ( )

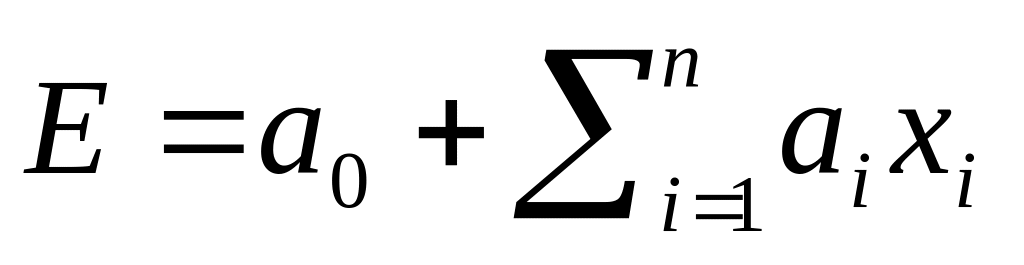• Мультипликативные модели ( )

• Степенные модели ( )

в первых двух группах коэффициенты a₁,...,a_n выбираются на основании данных предыдущих проектов; в третьей группе: S – размер проекта (основной фактор), a, b – функции (как правило очень простые) других факторов трудозатрат.

Линейные модели не оправдали себя на практике и не раз подвергались объективной критике [5]. В частности, зависимость от большого числа факторов влияющих на разработку ПО имеет явно нелинейный характер, что приводит к явной неэффективности данного класса моделей. Мультипликативные модели (например модель Валстона-Феликса [12]) сложны в калибровке (рассчете и уточнении коэффициентов) и не нашли обширного практического применения. В силу указанных причин, мы не будем далее рассматривать методы данных классов, а кратко опишем один из наиболее популярных и эффективных степенных алгоритмических методов.

7. COCOMO

COCOMO (COnstructive COst MOdel) и её производные являются пожалуй самыми популярными алгоритмическими моделями для оценки трудоемкости разработки ПО, которые де-факто стали стандартом. Модели относятся к классу степенных (см. выше). Базовая модель была представлена в 1981 г. Барри Боемом (Barry Boehm) [1]. С момента своего появления модель постепенно эволюционировала и можно обозначить основные этапы её развития следующим образом:

1. Базовая модель COCOMO. Размер проекта S измеряется в LOC (KLOC), а трудозатраты в человеко-месяцах. Cоздана на основе анализа статистических данных 63 проектов (в основном Министерства Обороны США) различных типов. Используется три набора параметров {a, b} в зависимости от сложности разрабатываемого программного обеспечения:

   1. Для простых, легко понимаемых проектов, а = 2.4, b = 1.05

   2. Для сложных систем, a = 3.0, b = 1.15

   3. Для встроенных систем, a = 3.6, b = 1.20.

Модель была проста в использовании, но не обеспечивала должной точности.

2. Детализированная модель COCOMO. Уточнены наборы параметров {a, b}, и, кроме того, общая формула приняла форму , где M – уточняющий коэффициент, рассчитывающийся как произведение 15-ти поправочных факторов из 4-х категорий (факторы конечного продукта, вычислительной среды, персонала, проекта) варьирующихся в диапазоне от 0.7 до 1.66, которые могут быть найдены в специальной таблице. Эти изменения базовой модели позволили существенно улучшить точность оценки, особенно в случае применения метода к отдельным компонентам, а не к системе в целом.

3. COCOMO II. (1997 г.) Имеет много общего со своей предшественницей, однако во многом основана на новых идеях, а также адаптирована к современным методологиям разработки ПО (в частности, если COCOMO подразумевала только каскадную модель жизненного цикла, то COCOMO II также пригодна для спиральной и итеративной). При построении COCOMO II для обработки статистических данных использовался Байесовский анализ, который дает лучшие результаты для программных проектов, характеризующихся неполнотой и неоднозначностью, в отличие от многофакторного регрессионного, примененного в COCOMO. Также в ней допускается измерять размер проекта не только числом строк кода (LOC), но и более современными функциональными и объектными точками (см. выше). Помимо прочего, при расчете показателей COCOMO II учитывает уровень зрелости процесса разработки в соответствии с моделями SEI CMM/CMMI. [15]

Общее плановое время разработки в модели COCOMO рассчитывается по формуле:

(8)

где c – коэффициент сжатия нормального графика, а p – функция зависящая от факторов масштаба системы. Детальное описание модели COCOMO II может быть найдено в [[1]].