1.3. Принципы цифрового управления

На риc. 1.7 показана обобщенная схема система автомати­ческого управления (САУ). Чтобы спроектировать реальную циф­ровую систему управления (ЦСУ) для того или иного ОУ, не­обходимо, прежде всего, ответить на вопрос, с какой целью и какими средствами предполагается управлять объектом, и выб­рать соответствующие принципы управления. Последние суще­ственно различаются в зависимости от характеристик ОУ, от характера информации, получаемой об объекте в процессе его работы, от характера окружающей среды и имеющейся инфор­мации об ее изменении в процессе работы, от наличия и полноты математического описания ОУ и окружающей среды и, что самое главное, от задачи, поставленной перед САУ, т. е. от цели управления.

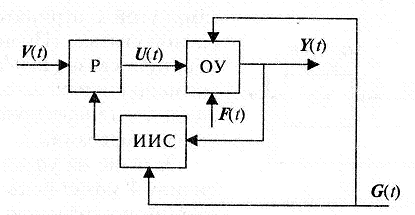
Рис. 1.7. Функциональная блок-схема САУ

Можно выделить следующие основные задачи, которые мо­гут быть поставлены перед САУ: стабилизация управляемых ве­личин, слежение за некоторой измеряемой величиной, про­граммное управление состоянием ОУ, самонастройка САУ на оптимум какого-либо параметра, управление целесообразным поведением ОУ, управление живучестью САУ.

Задача стабилизации может решаться различными путями в зависимости от имеющейся информации от ОУ и о внешних воздействиях на него. Если все внешние воздействия на ОУ кон­тролируются и могут быть измерены, а свойства ОУ и его дина­мические характеристики известны, то управление может вес­тись по возмущению в соответствии с функциональной схемой, показанной на рис. 1.8.

Рис. 1.8. Схема системы стабилизации по возмущению

В этом случае F≈ 0 и задача управления решается путем нахождения функции управления U(G), при которой обеспечивается условие:

Y= = const, (1.2)

где — эталонное или требуемое значение упрашгяемой величины, соответствующее заданию V.

Регулятор (Р), выполняющий условие (1.2), обеспечивает стабилизацию управляемых величин или их инвариантность, т. е. независимость от внешних воздействий с некоторой погрешно­стью , которая должна быть минимально возможной. Это дос­тигается путем решения соответствующей оптимизационной за­дачи для нахождения параметров регулятора, обеспечивающих минимум . При наличии неконтролируемых возмущений (F 0) и при недостаточно полном математическом описании ОУ управление по возмущению не может обеспечивать требуе­мой стабилизации управляемых величин. В этом случае применяет­ся принцип управления по отклонению в соответствии с функ­циональной схемой, показанной на рис. 1.9. Управляющее воздействие на ОУ U(e) зависит от разности между управляе­мой величиной и заданием (Е = V— Y) и направлено в сторону уменьшения этой разности. Образующаяся связь между выходом ОУ и входом Р называется обратной связью, а так как выход ОУ вычитается из задания, то такая обратная связь называется от­рицательной. Поэтому САУ, показанная на рис. 1.9, является замкнутой с отрицательной об­ратной связью. (Положительная обратная связь (F = V + Y) так­же используется в технике для создания генераторов периоди­ческих колебаний.).

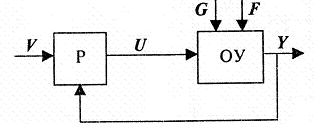
Рис. 1.9. Схема системы стабилизации по отклонению

З адание на управляемую величину V может быть либо равно требуемому значению Y, либо несколько превышать это значение для того, чтобы обеспечить зна­чение Е, достаточное для рабо­ты регулятора, параметры ко­торого определяются путем решения соответствующей оп­тимизационной задачи. Для по­вышения точности работы САУ применяются комбинирован­ные системы с функциональ­ной схемой, показанной на рис. 1.10, в которой сочетаются прин­ципы управления по возмущению и по отклонению.

Рис. 1.10. Схема комбинированной системы стабилизации

З адача слежения за изменениями измеряемой величины например координат самолета, выполняется с помощью следя­щей системы. Основным требованием, предъявляемым к следя­щей системе, является поддержание минимума погрешности d(t), определяемой как разность между заранее неизвестным законом изменения измеренной величины V(t) и управляемой величи­ной Y(t). Следящие системы обычно представляют собой замк­нутые системы управления по отклонению (рис. 1.11). В них за­дающее воздействие V(t) однозначно определяет эталонное значение

управляемой величины Y(t). Поэтому режим стабили­зации можно считать частным случаем слежения, когда должно выполняться равенство .

Программное управление какой-либо управляемой величи­ной в зависимости от наличия математического описания ОУ и неконтролируемых внешних воздействий может осуществляться разомкнутыми и замкнутыми системами.

Если существует точное математическое описание ОУ, а все внешние воздействия контролируются и путем регулирования по возмущению их влияние может быть сведено к минимуму (прак­тически до нуля), то программное управление осуществляется

п о разомкнутой системе, жестким управлением. При этом задает­ся такой закон изменения управляющей величины U(t), который обеспечивает требуемый закон изменения управляемой величи­ны Y(t), так как если известны уравнения, описывающие поведе­ние ОУ, то по заданному закону изменения управляемой величи­ны Y(t) = можно вычислить требуемый закон изменения управляющей величины U(t).

Рис. 1.12. Схема разомкнутой системы программного управления

Применение программного устройства (ПУ) (рис. 1.12), за­дающего эту зависимость, вычисленную заранее, обеспечивает выполнение программного управления. Кроме того, зависимость U(t) может вычисляться автоматически, в процессе функцио­нирования ОУ, с помощью специального вычислительного ус­тройства (управляющей вычислительной машины (УВМ) с опе­рационной системой реального времени), моделирующего ОУ (рис. 1.13). На вход модели (М) подаются задающее воздействие V(t) и контролируемые возмущения G(t). С помощью модели вычисляется зависимость U(t), подаваемая на ОУ и обеспечива­ющая эталонный закон управления Y₃(t). При этом, очевидно, что модель ОУ должна работать значительно быстрее самого ОУ.

Л юбая неточность математического описания ОУ или нали­чие неконтролируемых воздействий F(t) на ОУ приводит к нарушению соответствия между Y₃(t) и Y(t), т. е. к невыполне­нию требуемого закона изменения управляемой величины. В этом

Рис. 1.13. Схема разомкнутой системы программного управления с моделью ОУ

случае следует применять принцип программного управления по отклонению, т. е. использовать замкнутую САУ (рис. 1.14). Те­перь в регулятор (УВМ) подаются задающее воздействия V(t) и измеренные значения управляемой величины Y(t). В результате их сравнения УВМ вырабатывает такое управляющее воздействие U(t), которое обеспечивает минимальное значение рассогласо­вания E(t) = V(t) — Y(t). Функция V(t) хранится в памяти УВМ, выполняющей функцию программного устройства.

Рис. 1.14. Схема замкнутой системы программного управления

Для повышения точности управления могут использоваться комбинированные САУ, показанные на рис. 1.15. Описанные ра­нее системы автоматической стабилизации можно рассматри­вать как частный случай программных систем, в которых про­грамма не зависит от времени, т. е. V(t) = const.

Самонастройка или адаптация осуществляется адаптивны­ми САУ. Задачи, стоящие перед такими системами, значитель­но сложнее.

П ервой задачей является поддержание экстремума управляе­мой величины. Для этой цели на ОУ могут подаваться пробные воздействия от регулятора (Р), анализируется знак изменения управляемой величины Y, вычисляется управляющее воздействие

Рис. 1.15. Схема комбинированной системы программного управления

U , приближающее режим к точке экстремума, и подается на ОУ (рис. 1.16).

Рис. 1.16. Схема системы адаптации с экстремальным регулятором

Таким образом, САУ ав­томатически поддерживает режим, близкий к оптимальному, при ко­тором все dyjdu_j ≈ 0. Устройства, обеспечивающие режим работы ОУ, близкий к оптимальному, на­зываются автоматическими опти­мизаторами или экстремальными регуляторами.

Подобные регуляторы применяются для ОУ, имеющих экстремальные характеристики и существенные, но медленно меняющиеся неконтролируемые возмущения, приводящие к из­менению экстремальных характеристик. При этом можно считать, что за время прихода за счет управления к экстремуму характеристики ОУ изменяются несущественно.

Второй задачей самонастройки является поддержание опти­мальной работы САУ но условию ее максимального быстродей­ствия. В этом случае показателем экстремума является время, в течение которого система приходит в соответствие с измене­нием задающего воздействия V(t). Это время может анализиро­ваться с помощью специального устройства самонастройки (С), изменяющего параметры регулятора (Р) таким образом, чтобы время регулирования стало минимальным (рис. 1.17). Параметры регулятора R изменяются за счет воздействия М, вычисляемого устройством самонастройки (программой УВМ) по результатам измерения Y(t), R(t) и вычисления времени реакции ОУ на проб­ные задающие воздействия V.

Рис. 1.17. Схема системы самонастройки на максимальное быстродействие

Объект управления вместе с регулятором в этом случае рас­сматривается как новый объект экстремального управления бо­лее высокой категории, управляемый устройством самонастройки (УС). В этом случае управляемыми величинами являются показа­тели качества переходных процессов, а также V, вычисляемые в УС на основании Y(t)и R(t), а управляющей — М, подаваемой в Р для настройки его параметров. Таким образом, рассматрива­емую систему можно разбить на две подсистемы, из которых одна управляет другой.

Управление целесообразным поведением характерно для сложных многосвязанных систем с элементами искусственно­го интеллекта. Как правило, четкое математическое описание таких систем связано с большими трудностями. Поэтому по­добные системы часто относят к классу интеллектуальных сис­тем управления (ИСУ), описываемых как нечеткие системы автоматического управления, либо как человеко-машинные си­стемы.

При создании САУ целесообразным поведением интеллек­туальных систем необходимо, прежде всего, решать следующие проблемы:

• Проблему интеллектуализации управления стратегического уровня, обеспечивающего планирование целесообразного пове­дения. Она связана с решением задач по выбору стратегии выпол­нения требуемого задания и формирования последовательности действий, необходимых для его реализации. Кроме того, данный уровень должен обеспечивать оперативную коррекцию поведе­ния в зависимости от изменений внешней среды и в самой ИСУ, например, из-за повреждений. Функционирование ИСУ на этом уровне требует наличия развитых способностей к приобретению знаний о закономерностях окружающей обстановки, к интерпре­тации, классификации и идентификации возникающих ситуаций, к анализу и запоминанию последствий своих действий, исходя из опыта работы (свойство самообучения).

Проблему интеллектуализации управления тактического уровня, которая в первую очередь касается поиска решения одной из ключевых задач, связанных с планированием марш­рутов и траекторий продвижения к цели в неполностью опре­деленных условиях, в том числе и с различными препятствия­ми, с учетом динамики исполнительных подсистем и текущих изменений среды функционирования. При этом должно обес­печиваться не только продвижение к цели по априорно задава­емым маршрутам и траекториям, но и необходимые произ­вольные изменения продвижения к заданному целевому объекту.

• Проблему интеллектуализации управления исполнитель­ного уровня, которая связана с обеспечением активной адапта­ции управления исполнительными механизмами к изменениям нагрузочных характеристик, к вариациям собственных парамет­ров и параметров среды функционирования.

Интеллектуальная сенсорная информационно-измеритель­ная система должна обеспечивать замыкание контуров управле­ния различных уровней путем формирования соответствующих афферентных потоков. Основной проблемой интеллектуализа­ции такой системы является определение степени адекватности преобразуемой сенсорной информации целям функционирова­ния ИСУ и степени достоверности отображения как ее внешней среды, так и внутреннего состояния объектов управления, а также обеспечения системы способностью к адаптации.

В настоящее время для решения перечисленных проблем в ИСУ используют проблемно-ориентированные экспертные си­стемы в качестве интеллектуальных экспертных регуляторов (ЭР) каждого из уровней управления. Общей отличительной чертой таких регуляторов является возможность инициализации тех про­граммно реализованных алгоритмов управления или распозна­вания, выбор которых в той или иной ситуации представляется наиболее оправданным. Поэтому важнейшим среди множества принципиальных вопросов построения ЭР является определе­ние объема выполняемых функций, синтез архитектуры по­строения, формирование базы алгоритмов и соответствующей базы знаний, конструирование машины логического вывода, обеспечивающей режим реального времени.

Д ля обеспечения решения возлагаемых на ЭР задач после­дние функционально должны содержать следующие основные модули (рис. 1.18): супервизор (СВ), базу знаний (БЗ), базу алгоритмов (БА), базу данных (БД), машину логического вы­вода (МЛВ), и контроллер (К) для связи с аппаратными сред­ствами систем управления. Кроме того, ЭР может содержать имитационную модель (ИМ), анализатор (А) и контроллер адаптации (КА) для обучения и адаптации к изменяющимся условиям функционирования.

Рис. 1.18. Схема интеллектуальной системы управления

Супервизор должен обеспечивать выбор одного из режимов работы, включая интерфейс с пользователем (для наполнения базы знаний, определения целей и алгоритмов управления и пр.), настройку контуров управления, обучение и собственно функционирование, предусматривающее обработку данных, идентификацию, коррекцию контуров управления, оценку ка­чества проведенной коррекции.

База знаний должна содержать знания о динамике объекта управления, диапазоне входных и возмущающих сигналов, алгоритмах базы алгоритмов. База алгоритмов должна содер­жать множество алгоритмов управления и идентификации. База данных должна содержать информацию о целях управ­ления и о текущем состоянии системы и процесса ее функ­ционирования.

Машина логического вывода должна обеспечивать эксперт­ные заключения по управлению в режиме реального времени.

Исходя из основной функции, а именно — решения задачи проектирования оптимального процесса управления, можно выделить следующие основные типы интеллектуальных систем управления с ЭР.

Простейшей ИСУ является система с жесткой логикой. В такой системе база знаний (БЗ) неизменна и задачей ЭР явля­ется обеспечение функционирования регулятора (Р) в оптималь­ном режиме, путем логического анализа данных, поступающих из сенсорной информационно-измерительной системы (СИИС), связанной с объектом управления (ОУ), и базы данных (БД). БЗ в такой системе представляет собой набор правил, набранных пользователем-проектировщиком в процессе создания ИСУ и не изменяющихся в процессе функционирования. Машина ло­гического вывода (МЛВ) анализирует эти правила, используя данные БД, пополняемые из СИИС, и принимает решения об использовании того или иного алгоритма из базы алгоритмов (БА). Супервизор (СВ) по выбранному алгоритму вырабатывает задающие воздействия, подаваемые через контроллер (К) в ре­гулятор и обеспечивающие оптимальное функционирование системы.

При необходимости адаптации параметров регулятора под изменяющиеся внешние условия, параметры объекта управле­ния (ОУ) и параметры исполнительных механизмов (ИМ) струк­тура ИСУ усложняется, так как теперь на регулятор поступают не только сигналы задания, но и сигналы адаптации — из блока настройки СВ через тот же или дополнительный контроллер адап­тации (КА). В этом случае БЗ должна быть дополнена правилами для принятия решения об изменении настройки регулятора, а БА должна быть дополнена соответствующими алгоритмами адаптации. Решения по прежнему принимает МЛВ, а СВ допол­нительно с помощью блока настройки по выбранному ранее алгоритму вырабатывает сигналы адаптации. Такие ИСУ отно­сятся к классу адаптивных систем.

При необходимости вмешательства оператора в процесс функционирования ИСУ или в процесс управления СВ через блок интерфейса с пользователем может изменять и/или допол­нять содержимое БД и БЗ, тем самым корректируя задающие воздействия, вырабатываемые блоками настройки и функцио­нирования СВ. Такие ИСУ относятся к классу обучаемых чело­веко-машинных систем.

В ряде случаев МЛВ ИСУ может выбирать такие алгоритмы управления и/или адаптации, которые требуют при выработке задающих воздействий сравнения сигналов из СИИС с сигнала­ми из имитационной модели (ИМ) ОУ. В этом случае ЭР допол­няется блоком имитационного моделирования, связанного с ос­тальными блоками ЭР и СИИС. Такие ИСУ относятся к классу систем управления с имитационными моделями в контуре уп­равления.

Наконец, наиболее функционально полной ИСУ является структура, ЭР дополнительно снабжен анализатором (А) послед­ствий принятия решения, который анализирует последствия уп­равляющих воздействий на ОУ, сравнивает их с реакциями блока ИМ на такие же воздействия, а в ряде случаев и с реакцией оператора, и по результатам анализа корректирует БЗ и/или БА, а иногда и БД. Такие ИСУ относятся к классу самообучающихся систем.

Управление живучестью наиболее полно используется в интеллектуальных системах.

К основным принципам, которые могут использоваться в ИСУ для регулирования живучестью, относятся: адаптация, динамический естественный отбор или горячее резервирование, стресс, компенсация и заимствование, ступор или включение аварийного режима.

Принцип адаптации традиционно используется как в жи­вых организмах, так и в управляемых системах для обеспечения приспосабливаемости к изменяющимся внешним условиям фун­кционирования [4].

ИСУ, как и любая целеустремленная система, формирует поведение Y(t), исходя из заложенной при проектировании в память ИСУ генетической программы U_r, обеспечивающей фун­кционирование системы, исходя из внутреннего текущего со­стояния системы X(t) и изменяющихся во времени внешних воздействий со стороны окружающей среды, в том числе дей­ствий оператора FJ):

.

Кроме того, поведение любой ИСУ корректируется за счет гибкой реакции на изменяющиеся во времени внешние условия и внутреннее состояние. Появляющиеся при этом отклонения Y(t) в поведении формируются в основном за счет выявления отклонений от прогнозируемых внешних воздействий F(t) и внутреннего текущего состояния X(t), а в ряде случаев и за счет выявления нарушений (сбоев и повреждений) генетиче­ских программ U_r:

Y(t) = f( ).

Наиболее изученной и часто встречающейся задачей управ­ления живучестью является адаптация, когда U_r(t) отсутству­ет, X(t) — минимально, а F(t) — максимально из-за нестацио­нарности среды, ее активного противодействия или из-за вмешательства оператора в процесс функционирования. В этом случае можно считать, что Y(t) =f( ) и сигналом для вклю­чения механизма адаптации служит наблюдаемое превышение сверх допустимых норм изменений внешней среды: F(t) > .

Принцип горячего резервирования, аналогичный динами­ческому естественному отбору, существующему в живых орга­низмах, также традиционно используется в системах управле­ния для обеспечения живучести при отклонениях внутреннего состояния системы из-за различных поломок и отказов. Задача обеспечения живучести или надежности функционирования системы, когда U_r отсутствует, влияние отклонений окружа­ющей среды F(t) минимально, а отклонение внутреннего со­стояния Х(t) максимально, т. е. когда можно считать, что Y(t)=f( ) поставлена достаточно давно и в значитель­ной степени изучена [5].

Сигналом для включения механизма динамического есте­ственного отбора, т. е. переключения каналов и блоков на ре­зервные, служит наблюдаемое превышение сверх допустимых норм изменений внутреннего состояния: X(t) > x_доп.

Принцип стресса, аналогичный стрессу у человека, ис­пользуется в ИСУ для управления живучестью сравнительно недавно. Подобная задача управления живучестью функцио­нирования системы возникает, когда отклонениями в изме­нениях окружающей среды F(t) и внутреннего состояния можно пренебречь, а отклонения в поведении опреде­ляются в основном изменениями, сбоями генетических про­грамм .

Включение механизма стресса приводит к переводу систе­мы в резервный режим, при котором качество функционирова­ния системы и (или) ее надежность резко уменьшаются, напри­мер, падает точность, энергетический ресурс, ослабевают усилия неперемещения и т. п., но система в целом продолжает целе­устремленно функционировать. Поэтому очень важно правиль­но определять моменты включения этого механизма, т. е. четко выявлять Ur(t) в процессе функционирования и в про­цессе проектирования.

Принцип компенсации и заимствования, когда после ана­лиза изменения поведения Y(t) для обеспечения живучести системы производится подключение к внешним источникам ресурсов, например к внешним базам данных, источникам пи­тания и др., в неавтоматическом режиме, т. е. операторами, используется давно [6]. Такая задача обеспечения живучести фун­кционирования системы возникает, когда изменения U. от­сутствуют, а изменения F(t) и K(t) выходят за информацион­ные диапазоны и не могут быть компенсированы за счет собственных ресурсов. В этом случае можно считать, что Y(t) = f( ) и сигналом для включения механизма ком­пенсации и заимствования служит наблюдаемое изменение по­ведения сверх допустимых норм Y(t) > , превышающих внутренние ресурсы. Включение этого режима связано со зна­чительными затратами, потерей автономности функциониро­вания, а также с ухудшением ряда существенных характерис­тик, например, быстродействия, мобильности и др. Поэтому очень важно правильно выявлять моменты наступления ситуа­ции включения механизмов компенсации и заимствования.

Принцип ступора или включения аварийного режима может использоваться в ИСУ для обеспечения живучести подобно тому, как это происходит у человека при бредовом состоянии [7]. Такая задача управления живучестью системы возникает, когда откло­нения в изменениях окружающей среды и внутреннего со­стояния превышают информационные диапазоны и одно­временно наблюдаются сбои генетических программ т. е.

В этом случае система после анализа начинает игно­рировать некоторую информацию или ее преднамеренно иска­жает из-за наличия сбоев , но добивается выполнения основной цели генетической программы — продолжения жиз­ненного цикла, несмотря на резкое ухудшение качества функ­ционирования и отказ от менее жизненно важных функций. На­пример, система становится очень медленно действующей, ослабевают усилия на перемещения, система отказывается от некоторых перемещений и т. п. При ступоре тенденциозен не только отбор, но и переработка информации, что выражается, в частности, в крайней избирательности извлечения информа­ции из памяти. Обычно этот режим возникает при существен­ных изменениях внутреннего состояния и значительных сбоях генетических программ .