Федеральное агентство по образованию

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В ПОЛИТЕХНИЧЕСКОМ УНИВЕРСИТЕТЕ

Выпуск 1

А.Е. ГОРОДЕЦКИЙ В. В. КОЗЛОВ Ю.Н. АРТЕМ ЕМКО ИЛ. ТАРАСОВА

ВЫЧИСЛЕНИЯ В СИСТЕМАХ УПРАВЛЕНИЯ

Рекомендовано Учебно-методическим объединением по университетскому политехническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки 220100 "Системный анализ и управление"

Санкт-Петербург Издательство Политехнического университета 2006

УДК 681.3 (075.8) ББК 32.818я73 Г 701

Рецензенты: Член-корреспондент РАН, профессор СПбГПУ Ю.М. Смирнов Доктор технических наук, профессор В.В. Александров (СПИИ РАН)

Городецкий А. Е., Козлов В. В., Артеменко Ю.Н., Тарасова И.Л. Вычис­ления в системах управления: Учеб. пособие. СПб.: Изд-во Политехи, ун-та, 2006. 464 с. (Информационные технологии в политехническом университете. Вып. 1).

ISBN 5-7422-1275-5

Пособие соответствует авторским курсам дисциплин "Управляю­щие ЭВМ и комплексы" и "Интегрированные системы автоматизации научно-производственной деятельности" направления магистерской подготовки 220100 "Системный анализ и управление".

Изложены вопросы организации вычислений в системах управле­ния. Главное внимание уделено проблемам вычислений в режиме ре­ального времени и параллельным вычислениям. Проведен анализ раз­личных архитектур вычислительных устройств с операционными системами реального времени. Даны примеры применения различных вычислительных устройств в системах управления. Описаны средства интеллектуализации и оптических вычислений. Рассмотрены вопросы развития нано- и молекулярных вычислительных средств.

Предназначено для студентов высших учебных заведений, обуча­ющихся по направлению магистерской подготовки 220100 "Системный анализ и управление". Может быть использовано также для студентов и аспирантов, специализирующихся в области цифровых систем уп­равления и информатики.

Табл. 11. Ил. 192. Библиогр.: 69 назв.

Печатается по решению редакционно-издательского совета Санкт- Петербургского государственного политехнического университета.

© Городецкий А.Е., Козлов В.В., Арте­менко Ю.Н., Тарасова И.Л., 2006 © Санкт-Петербургский государственный ISBN 5-7422-1275-5 политехнический университет, 2006

ОГЛАВЛЕНИЕ

Введение…………………………………………………………………………………...4

Глава 1. Цифровые системы управления ………………………………………….....7

• Обобщенное описание задачи цифрового управления……………………....7

• Объекты управления…………………………………………………………..16

• Принципы цифрового управления.…………………………………………..21

• Математические модели цифровых систем управления……………………34

• Вычислительные методы решения задач оптимального управления……...50

Глава 2. Управляющие вычислительные системы………………………………….62

1. Обобщенное описание…………………………………………………………62

2. Математические модели вычислительных устройств………………………94

3. Микроконтроллеры и микро-ЭВМ………………………………………….109

4. Персональные вычислительные машины и супер­компьютеры…………...131

2.5 Управляющие вычислительные комплексы………………………………...179

Глава 3. Управление с использованием нейронных сетей………………………....195

1. Обобщенное описание ………………...195

2. Классификация нейронных сетей ………………...202

3. Математические модели нейронных сетей ………………...212

4. Решение задач управления в нейросетевом базисе ………………...223

5. Гибридные нейронные сети ………………...260

Глава 4. Возможности повышения эффективности управляющих

систем ………………...275

1. Программные средства интеллектуализации ………………...275

2. Управляющие нейрокомпьютеры ………………...297

3. Нанокомпьютеры ……………..….337

Глава 5. Примеры применения вычислительных устройств в системах

управления ……………..….370

1. Микропроцессорная система управления электродвигателем .. ……...…...370

2. Нечеткая адаптивная система управления скоростью движения

автомобиля…………………………………………………………………...…….389

3. Нечеткая система управления углом поворота автомобиля…………...…..420

4. Управляющий вычислительный комплекс радиотеле­скопа РТ-70………..435

Библиографический список ………………....460

ВВЕДЕНИЕ

В последние годы вычисления играют все большую и большую роль в системах управления. Это объясняется прежде всего все возра­стающей сложностью современных систем управления, для функ­ционирования которых требуется не только вычислять традицион­ные скорости и ускорения, связанные со взятием производных и интегрированием, но и решать сложные задачи идентификации объектов управления и среды функционировании в условиях не­полной информации, а также находить оптимальные управляю­щие воздействия в условиях ограниченности временных и вычис­лительных ресурсов и большой изменчивости окружающей среды.

Теория и практика применения средств вычислительной тех­ники в системах управления в последнее время наталкиваются на предельные возможности ведения процесса управления в ре­альном времени с использованием традиционных вычислите­лей фон-неймановского типа. Это объясняется, во-первых, по­стоянным повышением к точности и скорости вычислений, а во-вторых — усложнением вычислительных задач. Последнее особенно характерно для интеллектуальных и человеко-машин­ных систем управления.

Достижения микроэлектроники и информатики стимули­руют практическую реализацию многоядерных процессоров и суперкомпьютеров, обеспечивающих принципиально новые архитектуры и алгоритмы параллельных вычислений, а также переход на нано технологический уровень изготовления элемен­тов вычислительных устройств.

Поскольку суперкомпьютеры, нейронные сети, нейроком­пьютеры и нанокомпьютеры занимают особое место среди управляющих вычислительных машин и в современных систе­мах интеллектуального управления выполняют важнейшие вы­числительные функции, этим вопросам в данной монографии уделяется наибольшее внимание.

Учебное пособие может быть рекомендовано для студентов старших курсов технических университетов, обучающихся по на­правлениям "Системный анализ и управление" и "Автоматиза­ция и управление". Так же она может быть полезна и для студен­тов по направлению "Информатика и вычислительная техника", и поэтому первая глава пособия содержит основные сведения из теории цифрового управления. Пособие состоит из пяти глав.

В главе 1 даны элементы теории цифрового управления, включая описание принципов построения систем цифрового управления, анализ их математических моделей, рассмотрение приемов и методов анализа статических и динамических харак­теристик, а также методов синтеза систем управления с задан­ными свойствами. Особое внимание уделяется методам управле­ния в условиях неопределенности.

В главе 2 приводится обобщенное описание управляющих вычислительных машин. Описываются математические модели блоков вычислительных машин, строящихся на основе конеч­ных автоматов. Описываются особенности организации вычис­лительных процессов и архитектур современных микроконтрол­леров, одноплатных микро-ЭВМ, персональных и супер­компьютеров, а также вычислительных комплексов с анализом сетевых средств.

Глава 3 посвящена нейросетевому подходу к организации вычислений в системах управления. Проводится классификация нейронных сетей, описываются их математические модели. По­дробно излагаются методы решения управленческих задач в нейросетевом базисе, в том числе и нечетких задач управления.

В главе 4 дан обзор методов повышения эффективности вы­числений в сложных системах управления. Описываются совре­менных программные средства интеллектуализации управления, управляющие нейрокомпьютеры. Анализируются возможности и пути создания управляющих нанокомпьютеров.

В главе 5 приводится ряд примеров применения вычислитель­ных устройств в системах управления — от простейших контроллеров до сложных управляющих вычислительных комплексов. Изло­жение материала этой главы построено таким образом, чтобы его можно было использовать при выполнении курсовых работ по си­стемам цифрового и интеллектуального управления.

Авторы выражают благодарность сотрудникам кафедры "Си­стем управления и информатики" СПбГУАП и кафедры "Ин­теллектуальных систем управления" СПбГПУ, а также профес­сору В. В. Дубаренко (Институт проблем машиноведения РАН) за ценные замечания и рекомендации, которые были учтены авторами при работе над рукописью, и заведующему кафедрой "Интеллектуальных систем управления" СПбГПУ члену-коррес­понденту РАН Ю. М. Смирнову за помощь в работе над рукопи­сью и при ее опубликовании.

Авторы

Глава 1

ЦИФРОВЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

1.1. Обобщенное описание задачи

цифрового управления

За время, прошедшее с момента, когда появилась первая ЭВМ, сменилось уже несколько поколений вычислительных машин. Менялись элементная база, конструктивные решения, языки программирования, программное обеспечение, но осно­вы архитектуры, заложенные при создании машин первого по­коления, практически без изменения перешли на машины по­следующих и успешно работают до настоящего времени. Нет сомнений, что идеи машин первого поколения еще послужат человеку. Однако все настоятельнее требуются системы, наде­ленные элементами интеллекта при обработке колоссального объема информации и в то же время работающие в темпе управ­ляемых процессов. Наиболее ярким примером таких систем яв­ляются системы автоматического (и/или автоматизированного) управления (САУ) техническими объектами с ЭВМ в контуре. В классической теории управления техническими объектами рас­сматривают различные варианты схем систем управления с ЭВМ в контуре. Для лучшего понимания принципа их построения рас­смотрим схему, представленную на рис. 1.1.

Система работает следующим образом. Под действием уп­равления U(t) объект движется по заданной программой траек­тории. Однако случайные, неуправляемые возмущения F(t) от­клоняют его движение от заданного. Отдельные компоненты вектора состояния объекта (t) измеряются датчиками, затем квантуются по амплитуде и по времени аналого-цифровыми

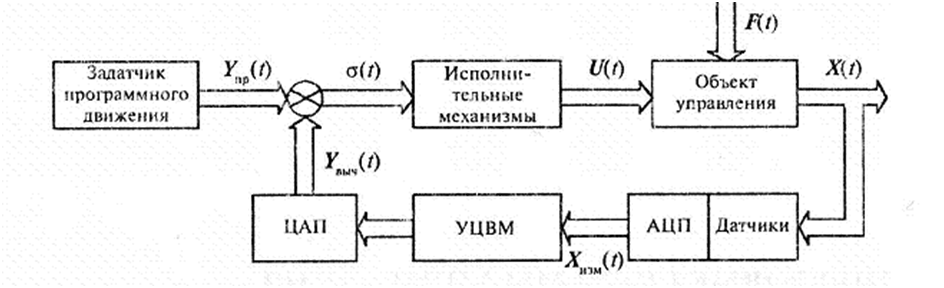
Рис. 1.1. Структура САУ с ЭВМ

преобразователями (АЦП) и передаются в управляющую вы­числительную машину (УЦВМ). Последняя, преобразовав изме­ренную входную информацию по заданному алгоритму, подает на узел сравнения вектор вычисленного воздействия Y_выч(t), со­ответствующий состоянию объекта на момент измерения. Узел сравнения вырабатывает сигнал ошибки Ω(t) и передает его ис­полнительным механизмам. Сформированное исполнительными механизмами управление U(t), воздействуя на объект, возвра­щает его на программную траекторию.

Очевидно, что УВМ, включенная в контур рассмотренной системы управления, должна удовлетворять следующим требо­ваниям:

осуществлять возложенные на нее вычисления с точностью, позволяющей системе нормально выполнять свои функции;

проводить обработку входной информации в темпе работы системы. Иначе говоря, УВМ должна выдавать результаты с тре­буемой точностью и работать в реальном масштабе времени.

Работа УВМ в реальном масштабе времени обеспечивается операционной системой реального времени (ОС РВ), являющейся фундаментом базового программного обеспечения любой ЭВМ. ОС РВ должна обеспечивать полный цикл жизни программного обеспечения: создание текста программы, ее компиляцию, по­строение, отладку, исполнение и сопровождение. Требования, которым должны удовлетворять любые ОС РВ, изложены в стан­дарте POSIX 1003.4 (Real Time Extensions for Portable Operating Systems) рабочего комитета IEEE, утвержденном ISO/IEC как международный стандарт 9945. Этот стандарт определяет операционную систему как систему реального времени (ОС РВ), если она обеспечивает требуемый уровень сервиса за вполне опреде­ленное, ограниченное время. Сказанное можно сформулировать таким образом, что ОС РВ должна быть предсказуема. Правиль­ная, но запоздалая реакция системы на внешнее событие зачас­тую может быть просто гибельной, например, в системе без­опасности атомной станции, системах управления воздушным транспортом и т. п. При этом важно не абсолютное время реак­ции системы, а то, что оно определено заранее. В системе управ­ления прокатным станом время реакции системы должно быть в пределах нескольких миллисекунд, а в системе контроля над окружающей средой — несколько минут. Однако оба эти приме­ра из области задач реального времени.

Современный уровень развития элементной базы вычисли­тельной техники позволяет выполнять задатчик программного движения и узел сравнения в виде программных модулей, раз­мещаемых в памяти той же УВМ, что и основной алгоритм об­работки входной информации. В этом случае УВМ будет выраба­тывать непосредственно сигнал ошибки и, очевидно, будет иметь большую вычислительную нагрузку. На рис. 1.2 представлена цифровая система управления с расширенными функциями УВМ.

Значительное повышение качества работы системы цифро­вого управления дает ее интеллектуализация. Систему управле­ния можно назвать интеллектуальной (ИСУ), если она способ­на на основе заложенных в ней знаний и полученных извне

Рис. 1.2. Схема цифровой системы управления

сведений сформулировать программу движения объекта и найти способ оптимальной реализации этой программы. При этом рез­ко возрастает объем вычислительных работ в ИСУ, и УВМ с последовательной архитектурой обычно не в состоянии его выполнить. Выход можно найти лишь в применении параллель­ных принципов организации обработки информации.

При синтезе систем управления одним из важнейших этапов является формализация описания объектов управления, среды функционирования, управляющих модулей и систем, а также целей управления. Процесс формализации обычно начинается с лингвистического описания задачи, построения систем логи­ческих уравнений, соответствующих поставленной и описанной лингвистической задаче и отражающих причинно-следственные связи между понятиями и отношениями, определение допусти­мых решений построенной системы уравнений и поиск наилуч­ших решений путем анализа атрибутов логических переменных, в том числе и таких их качественных элементов, как понятия и отношения с нечеткими границами, высказывания с много­значной шкалой истинности и др. Причем, чем сложнее описы­ваемые объекты, тем более нечеткие описания удается сформу­лировать на первом этапе. Далее, в процессе анализа задачи и пополнения знаний об объектах за счет проведения дополни­тельных исследований и изучения аналогов все или часть не­определенностей удается разрешить. При этом, если все неопре­деленности разрешаются, то получаются четкие модели, описываемые системами уравнений с вещественными или ком­плексными аргументами, а если не все неопределенности раз­решаются, то получаются нечеткие модели, описываемые сис­темами уравнений с логическими и (или) лингвистическими переменными. Исследование последних сопряжено с перебор­ными методами решений, не скалярными целевыми функция­ми и множественностью оптимальных решений, ранжирование или упорядочивание которых часто носит субъективный харак­тер. Однако попытки в этом случае решать задачи путем задания строгих границ "волевым" методом или искусственным введе­нием однозначности приводят к огрублению исходных данных, которое может способствовать получению четкого, но невер­ного результата, и поэтому нецелесообразны. Следовательно, формализованное описание систем управления может быть двух классов — четкое и нечеткое. В последнем случае управление при­нято называть нечетким (fuzzy control) [1]

При формировании задач управления, производят отобра­жение реальной задачи на некоторый формальный язык, явля­ющийся профессиональным языком лица, принимающего ре­шение, т. е. на язык разработчика Ф: Q₃ —> Q_p, где Ф-отображение множества Q₃ объектов отображаемой задачи (элементов и их взаимосвязей) в множество Q_p объектов языка разработчика (по­нятий, отношений, имен и т. д.). В случае, если отображение Ф устанавливает однозначное соответствие элементов множеств Q₃ и Q_p, имеет место задача управления в условиях определенности. В противном случае будет задача управления в условиях не пол­ной определенности или нечеткая задача управления (НЗУ), которая наступает, когда выполняется хотя бы одно из следую­щих условий:

где /. / — мощность множества, а — пустое множество. При этом в языке описания присутствует: синонимия (от греч. synonymous одноименный) — слова, раз­личные по звучанию, но тождественные или близкие по смыс­лу, а также синтаксические и грамматические конструкции, совпадающие по значению[2];

полисемия (от греч. поли — много и sema — знак) — наличие различных (но в какой-либо мере связанных) смыслов и (или) значений у одного и того же знака или знакосочетания [3]. На­пример, слово "лиса" обозначает животное и хитрого человека;

недостаточность или избыточность — наличие информации в изложении, не нашедшей отображения в модели, либо, на­оборот, наличие в модели понятий и (или) отношений, без которых можно обойтись при отображении и которым не соот­ветствуют какие-либо понятия и (или) отношения в исходном языке (исходной постановке задачи).

Рассмотрим наиболее часто встречающиеся виды неопреде­ленностей описания.

На начальной стадии изучения любой новой задачи инфор­мации о ней практически нет, т. е. неопределенность связана с неизвестностью информации.

По мере продвижения в изучении задачи на определенном этапе может быть недостоверность информации из-за того, что:

собрана не вся возможная информация (имеется ее непол­нота);

собрана не вся необходимая информация (имеется ее недо­статочность);

для некоторых элементов определены не их точные описа­ния, а лишь множества, к которым эти описания принадлежат (имеется недоопределенность);

ряд элементов задачи временно описан лишь по аналогии с уже решавшимися задачами (имеется лишь замещающее опи­сание, приводящее к неадекватности информации).

Данные типы неопределенности носят название "недостовер­ность", которая связана либо с тем, что процесс сбора информа­ции не закончен, либо с тем, что не хватает ресурсов, выделенных для сбора информации. Однако в принципе возможность результа­тивного продолжения сбора информации существует.

Дальнейшее изучение может привести к ситуации либо пол­ной определенности, либо неоднозначности, когда вся возмож­ная информация собрана, но полностью определенное описа­ние не получено и не может быть получено. Источниками возможной неоднозначности могут быть внешняя среда, т. е. фи­зическая неопределенность, либо используемый профессиональ­ный язык, т. е. лингвистическая неопределенность.

Физическая неопределенность может быть связана как со стохастической неопределенностью (случайностью) среды, так и с неточностью измерений вполне определенных величин, фиксируемых приборами с некоторой погрешностью (техни­ческой неточностью). При этом, как правило, законы распре­деления случайных величин, вызывающих физическую неопре­деленность задачи, можно установить, так как они носят вероятностный характер. Однако описания случайных процес­сов в виде корреляционных функций, либо спектральных плотностей в случае невыполнения условий стационарности и эргодичности получить не удается, что затрудняет формализацию указанных неопределенностей.

Лингвистическая неопределенность связана с использованием естественного языка при описании НЗУ. Эта неопределенность обусловливается необходимостью оперировать конечным числом слов и ограниченным числом структур фраз для описания за конечное время бесконечного множества разно­образных ситуаций, возникающих в процессе решения НЗУ. Лингвистическая неопределенность порождается, с одной сто­роны, множественностью значений слов (понятий и отноше­ний)языка, т. е. полисемией, а с другой — неоднозначностью смысла фраз.

Множественность значений слов может привести к непра­вильному присвоению атрибутов логическим переменным в базе знаний, если одним и тем же словом отображаются существенно различные объекты НЗУ. Такую ситуацию называют монимией. Например, слово "дом" обозначает жилое здание (сбе­жался весь дом), семья, люди, живущие вместе, их хозяйство (мы знакомы домами), место, где живут люди объединенные общими интересами (Общеевропейский дом), династия, род (Царствующий дом Романовых) и т. д.

Если же слова неточно определяют объекты НЗУ, напри­мер небольшой запас топлива — это может быть и 1 тонна и 1,1 тонны и т.д., то возникает ситуация нечеткости, описываемая нечеткими множествами.

Источниками неоднозначности смысла фраз могут быть сле­дующие неоднозначности:

синтаксическая — система языковых категорий, относящихся к соединениям слов и строению предложений [2]. Например: "казнить, нельзя помиловать" и "казнить нельзя, помиловать";

семантическая — значение, смысл отдельного слова, обо­рота речи [2]. Например, неспециалистам в вычислительной технике могут быть непонятны такие слова, как листинг, флоп­пи и др.

прагматическая — направление, ограничивающееся описа­нием событий в их внешней связи и последовательности без рас­крытия закономерностей их развития [2]. Например, в рекламе слышим "Бочкарев — правильное пиво". Теперь попробуем за­даться целью: производить правильное пиво. Что это означает?

В первом случае для уточнения смысла фраз достаточно уточ­нить или пополнить правила базы знаний дополнительными правилами синтаксиса. Так, в приведенном примере достаточно правильно поставить запятую и неопределенность устраняется.

Во втором случае может возникать поверхностная и глубин­ная неоднозначность. При поверхностной неоднозначности мо­гут быть понятны отдельные слова фразы, но вся фраза непо­нятна и для ее расшифровки требуются уточняющие смысл дополнительные фразы. При глубинной неоднозначности непо­нятны все отдельные слова фразы и для ее расшифровки требу­ется доопределение слов. При этом может быть либо разрешена неопределенность, либо мы перейдем к первому варианту не­однозначности, и тогда потребуются уточняющие смысл дополнительные фразы.

Наконец, прагматическая неопределенность связана с не­однозначностью использования синтаксически и семантически понятной информации для достижения целей управления или принятия решения. Так, в приведенном примере, очевидно, что поставленную цель выполнить нельзя, так как не определено понятие "правильное пиво".

Следует отметить, что учет физической неопределенности может усложняться проявлением лингвистических неопределен­ностей в описании: различные виды неопределенностей могут накладываться друг на друга. Кроме того, необходимо иметь в виду, что указанными типами неопределенности могут обла­дать любые элементы НЗУ.

В общем случае задача управления может быть охарактери­зована следующим кортежем: <Z, М, Р, К, Q, W>, где Z— множество альтернативных решений (законов управления); М — окружение выбора, т. е. среда задачи, в которую включены эта­лонная модель объекта управления, технических средств управ­ления и окружающей среды, в которой предполагается функци­онирование объекта управления; Р— система предпочтений эксперта или системы, принимающей решение, на базе кото­рой строятся критерии качества К, соответствующие целям уп­равления Q; W— необходимые способы действий (алгоритм), которые требуется выполнить над множеством альтернатив Z, например, найти наиболее предпочтительную, линейно упоря­дочить множество допустимых альтернатив и т. п., для того что­бы синтезировать управление, удовлетворяющее системе пред­почтений Р по построенному критерию качества К.

Альтернативным решением будем называть вариант реше­ния, удовлетворяющий ограничениям задачи управления и обес­печивающий получение требуемых параметров и характеристик управления, а средой задачи — эталонную модель объектов и системы управления, а также тех условий, в которых предпо­лагается функционирование системы, которые необходимо учи­тывать при формировании и решении задачи. При этом можно выделить следующие пять основных типов задач управления:

в условиях определенности, когда каждой альтернативе со­ответствует строго определенный исход,

в условиях риска, когда исход является дискретной или не­прерывной случайной величиной с известным законом распре­деления или хотя бы с известными числовыми характеристика­ми распределения,

в условиях неопределенности, когда исход является случай­ной логической переменной или функцией с известной вероят­ностью ее истинности или ложности,

в условиях неопределенности, когда исход является лингви­стической переменной, задаваемой кортежем < I, L, A, G, V>, где /— наименование лингвистической переменной, L— мно­жество ее значений или термов, представляющих собой наиме­нование нечетких переменных, областью определения каждой из которых является множество A, G — синтаксическая проце­дура, описывающая процесс образования из множества L но­вых, осмысленных для данной задачи управления значений лин­гвистической переменной, V— семантическая процедура, позволяющая приписать каждому новому значению, образуемо­му процедурой G, некоторую семантику путем формирования соответствующего нечеткого множества, т. е. отобразить новое значение в нечеткую переменную,

в условиях неопределенности, когда исход является ре­зультатом эволюции и скрещивания ряда альтернатив, каж­дая из которых может иметь исход либо в виде случайной логической переменной (функции), либо в виде лингвистической переменной.

Первую задачу будем называть классической задачей детер­минированного управления, вторую — классической задачей недетерминированного управления, третью — задачей логико-вероятностного управления, четвертую — задачей логико-линг­вистического управления и пятую — задачей эволюционно-генетического управления. Очевидно, что к задачам нечеткого управления относятся задачи с третьей по пятую и в общем виде их решением будет синтез алгоритма поиска ⱷ W из множе­ства альтернатив Z лyчшeгo закона управления f Z на основе оценок качества К, построенных с учетом системы предпочте­ний Р и среды задачи М: , где 2^Z— обозначает мно­жество всех подмножеств Z, а К^z— множество всех кортежей длиной от 2 до /Z/.