Лекция 7 уравнения электромагнитного переходного процесса синхронной машины

Переходный процесс в электрической машине может быть описан системой дифференциальных уравнений. Выбор системы координат определяется конкретными условиями решаемой задачи.

Дифференциальные уравнения равновесия ЭДС и падений напряжений в каждой из обмоток статора (А, В, С) и ротора (f):

U_А = - - R_Аi_А;

U_В = - – R_Вi_В;

U_С = - – R_Сi_С;

U_f = + R_fi_f,

где R_А, R_В, R_С, R_f – активные сопротивления контуров фаз А, В, С и обмотки возбуждения; Ψ_А, Ψ_В, Ψ_С, Ψ_f - результирующие потокосцепления контуров фаз А, В, С и обмотки возбуждения.

Потокосцепление обмотки фазы А выражается уравнением:

Ψ_А = L_Аi_А + M_АВi_В + M_АСi_С + M_Аfi_f ,

Ψ_В = M_ВАi_А + L_Вi_В + M_ВСi_С + M_Вfi_f ,

Ψ_С = M_САi_А + M_СВi_В +L_Сi_С + M_Сfi_f ,

Ψ_f = M_fAi_A + M_fBi_B + M_fCi_C + L_fi_f,

где L_А, L_В, L_С, – коэффициент самоиндукции обмотки фаз А, В, С; M_АВ, M_ВА, M_СА, M_СВ, M_СА, M_ВС, - коэффициент взаимоиндукции обмоток фаз А , В и С; M_Аf - коэффициент взаимоиндукции обмотки фазы А и обмотки возбуждения.

Во вращающейся машине коэффициенты L и M не являются постоянными коэффициентами и зависят от положения ротора относительно обмоток статора и, следовательно, являются функциями времени.

Закон изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора выражается синусоидальной функцией.

М_Аf = М_fА = М_Аfсоsγ

где γ – угол между магнитной осью фазы А и продольной осью ротора d.

Индуктивность обмотки фазы А определяют как

L_А = l₀ + l₂соs2γ

Взаимная индуктивность М_АВ = m₀ + m₂соs2(γ - π/3)

где l₀ и m₀ – постоянные составляющие соответствующих индуктивностей;

l₂ и m₂ – амплитуды вторых гармоник тех же индуктивностей.

Коэффииценты l₀ и m₀ и l₂можно выразить через индуктивности, которыми характеризуется синхронная машина

l₀ = ; l₂ = ;

Систему дифференциальных уравнений с переменными коэффициентами решить очень сложно. Для её решения существуют несколько способов. Мгновенные значения фазных величин (U, Ψ, i) можно получить как проекции фазных векторов на неподвижную ось времени t или как проекции обобщенного вектора f на неподвижные магнитные оси фаз А, В и С. Вектор f в общем случае может характеризовать фазные величины, изменяющиеся во времени по произвольному закону. Представление трехфазной системы векторов обобщенным вектором упрощает выражение связи между статором и ротором, что позволяет в дифференциальных уравнениях переходного процесса освободится от переменных коэффициентов.

Замена переменных

Представление фазных величин f_А, f_В, f_С через обобщенный вектор f возможно при условии:

f_А + f_В + f_С = 0.

Если сумма фазных переменных не равна нулю, то её целесообразно выразить через новое переменное f₀ : f_А + f_В + f_С = 3f₀. Нулевая составляющая во всех фазах одинакова и тождественна составляющей нулевой последовательности. Фазные переменные, выраженные через обобщенный вектор:

f_А = fcosα; f_В = fcos(α - 2π/3); f_c = fcos(α + 2π/3),

где α - угол между векторами f_А и f (Рис.1)

Рис.1. Обобщенный вектор трехфазной системы

Обобщенный вектор можно определить как

f²_А + f²_В + f²_С = (3/2) f²,

Откуда

f

Обобщенный вектор можно выразить и в двухосной системе координат. В качестве последней удобно выбрать декартовые ортогональные координаты х и у или d и q (cовмещенные с магнитными осями ротора генератора, рис.2.).

Преобразование координат соответствует замене переменных. Проекции вектора f на оси х и у:

f_Х = fcos(θ - α); f_У = fsin(θ - α),

где θ - угол между магнитной осью фазы А и осью Х.

А

d q

f f_A α

f_d γ

f_q

В С

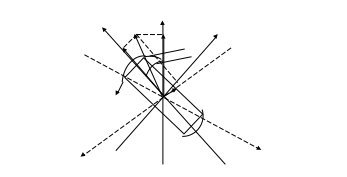
Рис.2. Преобразование координат

Применение новой системы координат сокращает переменные коэффициенты. Упрощения можно достичь, используя декартову систему координат, жестко связанную с ротором синхронной машины d, q и 0. Поскольку фазные обмотки, расположенные в осях d, q, неподвижны относительно ротора, индуктивности такой машины постоянны. Фазные переменные в системе координат d, q и 0:

f_А = cosγ + sinγ + f₀;

f_В = cos(γ - 2π/3) + sin(γ - 2π/3) + f₀;

f_С = cos(γ + 2π/3) + sin(γ + 2π/3) + f₀,

где γ = ω_сt + γ₀ – угол, характеризующий положение ротора в пространстве; ω_с - синхронная угловая скорость, γ₀ - начальный угол.

Фазные переменные напряжения, тока в системе координат d, q и 0:

U_А = cosγ + sinγ + U₀;

i_А = cos(γ - 2π/3) + sin(γ - 2π/3) + i₀;

Ψ_А = Ψ_dcos(γ + 2π/3) + Ψ_qsin(γ + 2π/3) + Ψ₀.

Подставляя фазные переменные в дифференциальное уравнение равновесия обмотки фазы А получим уравнения Парка-Горева

= - – Ψ_q – R ; (1)

= - + Ψ_d – R ;

= - – R ,

где , , – ЭДС трансформации, вызывается изменением величин потокосцеплений; Ψ_q , Ψ_d – ЭДС вращения (скольжения).

Потокосцепления в системе относительных единиц равны

где - индуктивность и индуктивное сопротивление нулевой последовательности машины.

Таким образом переход к новым переменным в координатах d, q, 0 позволил преобразовать систему дифференциальных уравнений равновесия ЭДС и падений напряжений, где все коэффициенты постоянны.

Уравнения (1) выражают основу теории двух реакций синхронной машины при электромагнитном переходной процессе.

Для самостоятельного изучения - тема: Схемы замещения синхронной машины в продольной и поперечной осях ротора для начального момента переходного процесса