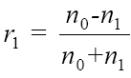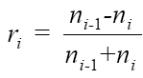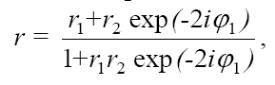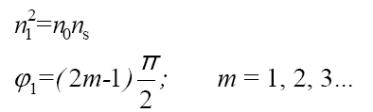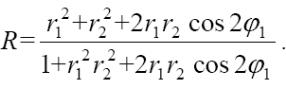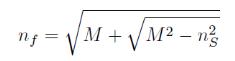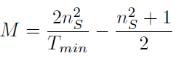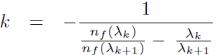1.4. Содержание отчета и обработка результатов

1. Кратко описать методики исследований.

2. Построить вольт-амперные и световые характеристики фоторезистора.

3. Привести измеренные значения _н и _сп, а также построить зависимость амплитуды импульса фототока от длительности светового импульса для фоторезистора.

4. Рассчитать кратность изменения сопротивления фоторезистора при 5 и 10 В, используя выражение (1.2).

5. Определить коэффициент усиления фоторезистора, пользуясь выражением (1.3) при  = 350 см²/(Вс), l = 0.1 см, U = 10 В и  = _сп/3.

6. Аппроксимировать световую характеристику фоторезистора выражением (1.1) и определить параметры A и x.

7. Из зависимости амплитуды фототока от длительности светового импульса определить длительность импульса _0.7, при которой амплитуда фототока уменьшается до уровня 0,7 от стационарного значения. Найти граничную частоту f_гр= 1/_0,7.

8. Построить вольт-амперные, световые и нагрузочные характеристики фотодиода.

9. Привести значения _н и _сп, а также построить зависимость амплитуды импульса фототока фотодиода от длительности светового импульса для вентильного и фотодиодного режимов работы.

10. По вольт-амперным характеристикам фотодиода определить его чувствительность, используя выражение (1.5).

11. Определить значение тока насыщения I_нас из выражения (1.6), подставив туда экспериментальные значения U_хх и I_кз при одинаковых значениях светового потока. Сравнить полученное значение со значением I_нас, найденным по вольт-амперной характеристике неосвещенного фотодиода.

12. Из нагрузочных характеристик определить R_н, при котором мощность фотодиода в вентильном режиме будет максимальной.

13. Определить _0,7 и f_гр для вентильного и фотодиодного режимов работы фотодиода при разных значениях сопротивления нагрузки.

1.5. Контрольные вопросы

Какова физика изменения проводимости полупроводника под действием света?

Как объяснить ход спектральной характеристики полупроводника?

Каковы физические основы работы фоторезисторов и фотодиодов?

Объясните световые характеристики фоторезисторов и фотодиодов.

Какие физические явления определяют инерционные свойства фоторезисторов и фотодиодов?

Как влияют сопротивление нагрузки и напряжение, приложенное к фотодиоду, на его инерционные свойства?

Какой режим работы фотодиода целесообразно использовать для измерения интенсивности оптического излучения и почему?

2. Исследование оптических свойств слоев тонкопленочных солнечных элементов

Целью данной работы является изучение оптических свойств слоев фотоэлектрических преобразователей на примере измерения спектров отражения и пропускания тонких пленок аморфного гидрогенизированного кремния и прозрачного проводящего оксида

2.1. Основные сведения об оптических свойствах солнечных элементах

Оптические свойства слоев СЭ, в частности, спектр коэффициента поглощения полупроводникового слоя, определяют их спектральную чувствительность, а следовательно и КПД СЭ. Оптические потери на отражение от лицевой поверхности полупроводникового слоя могут достигать порядка 30%. Поэтому в конструкции любых солнечных элементов присутствуют оптические слои – просветляющие покрытия, снижающие коэффициент отражения. Используются как однослойные, так и многослойные просветляющие покрытия. Так на рис. 2.1 представлены результаты упрощенного расчета спектров отражения для разного количества слоев антиотражающего покрытия СЭ со стеклянным покрытием, считая показатели преломления не зависящими от длины волны. Видно, что с увеличением числа слоев антиотражающего покрытия диапазон спектра с минимальным отражением расширяется.

В случае тонкопленочных солнечных элементов в основном используются одиночные слои прозрачных проводящих оксидов (ППО), которые одновременно играют роль и просветляющего покрытия и контактного слоя. При разработке конструкции тонкопленочных солнечных элементов необходимо проводить оптимизацию параметров слоев прозрачных проводящих оксидов с учетом двух, как правило, взаимоисключающих условий - максимальная проводимость слоя и минимальные оптические потери. Следовательно, исследование оптических свойства как самих слоев ППО так и СЭ, содержащих ППО, необходимо при разработке и оптимизации тонкопленочных СЭ. Следует заметить, что при создании тонкопленочных СЭ часто используется дополнительный метод уменьшения потерь на отражение – формирование текстуры, т.е. развитого рельефа поверхности. В данном случае значительно возрастает рассеяние света, что приводит к резкому снижению коэффициента прямого отражения. Однако, в этом случае необходимо проводить измерения коэффициента диффузного рассеяния.

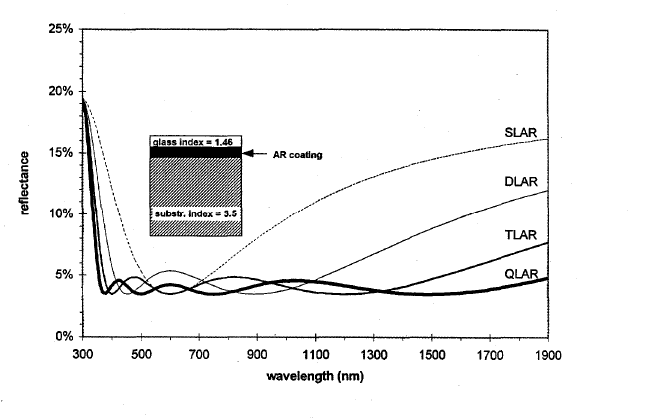
Рис.2.1. Расчетные спектры отражения для однослойного (SLAR), двухслойного (DLAR), трехслойного (TLAR) и четырехслойного ( QSLAR) антиотражающего покрытия.

Для проведения аналитического расчета коэффициента отражения однослойного покрытия рассмотрим самый простой случай без учета поглощения и дисперсии показателя преломления диэлектрических слоев. Показатели преломления окружающей среды и подложки обозначим через n₀ и n_s, соответственно, а слои пронумеруем по порядку от наружного слоя к подложке как изображено на рис. 2.2. Величины r и n - вещественные числа,

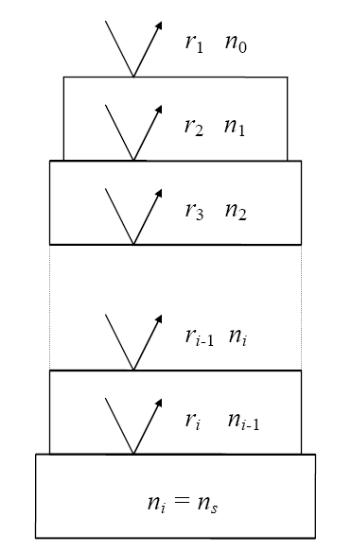
Рис. 2.2. Схематическое изображение двухслойной оптической системы

т. к. поглощение не учитывается. В многослойной оптической системе коэффициенты отражения Френеля будут выглядеть следующим образом:

(2.1).

Если свет падает нормально на прозрачную среду, покрытую одним прозрачным слоем, то амплитуда отраженного света характеризуется коэффициентом отражения:

(2.2),

где i – мнимая единица и  ₁ = 2π n₁d₁/λ, d₁ − геометрическая толщина слоя.

Коэффициент отражения будет равен нулю при n₀ = n_s (тривиальное решение), а также при:

(2.3),

Если m=1 то оптическая толщина n₁d₁ = /4 такое покрытие называется «четверть волновым».

Интенсивность отраженного света характеризуется:

	(2.4),
	(2.5),
	(2.6).

При разработке конструкции СЭ необходимо также учитывать поглощение в полупроводниковых и оптических слоях. Для определения коэффициента поглощения проводят измерение спектров пропускания T тонких пленок, нанесенных на прозрачную подложку. Так на рис. 2.3 представлен спектр коэффициента пропускания пленки аморфного гидрогенизированного кремния (a-Si:H) толщиной 500 нм. В области длинных волн, где практически отсутствует поглощение видны интерференционные максимумы и минимумы, положение которых определяется показателем преломления и толщиной пленки. В области коротких длин волн значительное поглощение приводит к резкому уменьшению коэффициента пропускания.

Рис. 2.3 Спектр коэффициента пропускания пленки аморфного гидрогенизированного кремния (a-Si:H) толщиной 500 нм.

Из закона сохранения энергии следует:

R + T + A =1, (2.7),

где A - энергетический безразмерный коэффициент поглощения системы. Если считать, что А определяется только поглощением в измеряемом слое, то

A= 1 - exp (-  d) (2.8),

 - коэффициент поглощения материала слоя (см^-1), d -толщина слоя (см).

Однако, формула 2.7 не учитывает отражения от обратной стороны образца. Коэффициент пропускания с учетом поглощения и отражения от обратной стороны образца может быть выражен следующим приближенным выражением:

T ≈ [(1- R)² exp (-  d)]/ [(1- R)² exp (-2  d)], (2.9)

которое может быть упрощено для случая сильного поглощения в полупроводниковом слое, когда многократным отражением можно пренебречь:

T ≈ (1- R)² exp (-  d) (2.10).

Измерив спектральные зависимости коэффициентов пропускания и отражения и зная толщину пленки, по формуле 2.10 можно получить спектральную зависимость коэффициента поглощения. Однако, данный подход справедлив только для больших значений коэффициента поглощения.

В случае сильного поглощения, когда интерфенционным эффектом можно принебречь показатель преломления измеряемой пленки может быть определен исходя из следующего выражения:

R=(n-1)²/(n+1)² (2.11)

И выражен следующим образом:

n=(1+ R+ R^1/2)/( 1- R) (2.12)

В области, где поглощением можно пренебречь и при наличии интерференционного эффекта показатель преломления подложки может быть определен из максимума пропускания (T_max):

(2.13)

Показатель преломления измеряемой пленки (n_f) может быть определен по минимуму пропускания (T_min) по следующий формуле:

(2.14),

где

(2.15).

Зная показатель преломления пленки можно определить ее толщину по положению интерференционных минимумов и максимумов исходя из следующего выражения:

(2.16),

где k – порядок интерференции, цело число - четное для максимумов и нечетное для минимумов. Определить порядок интерференции можно по двум соседним экстремумам, пользуясь следующим выражением:

	(2.17),
	(2.18).

Таким образом, по интерференционной картине может быть определена толщина образца, зная которую по формуле 2.10 можно построить спектральную зависимость коэффициента поглощения.

Для непрямозонных полупроводников в области собственного поглощения коэффициент поглощения имеет квадратичную зависимость от энергии фотонов:

  (h - E_g)²/ h (2.19).

По этой зависимости может проведена оценка ширины запрещенной зоны полупроводниковых слоев E_g.

Измерение спектров отражения и пропускания

Проведение измерения спектров коэффициента отражения и пропускания возможно различными способами. Можно выделить два основных способа: в первом используется источник монохроматического излучения; во втором на образец падает немонохроматическое излучение, которое после отражения от поверхности образца (или прохождения через образец) поступает на спектрометр.

Рассмотрим оптическую схему первого способа с использованием пары контрольных элементов, изображенную на рис. 2.4. Монохроматический свет последовательно, путем поворота сферического зеркала, направляется на первый контрольный фотоприемник (к1), а затем на второй контрольный фотоприемник (к2). На второй контрольный фотоприемник свет попадает после отражения от исследуемого образца. Таким образом, по результатам измерения фототоков контрольных фотоприемников и производится расчет коэффициента отражения:

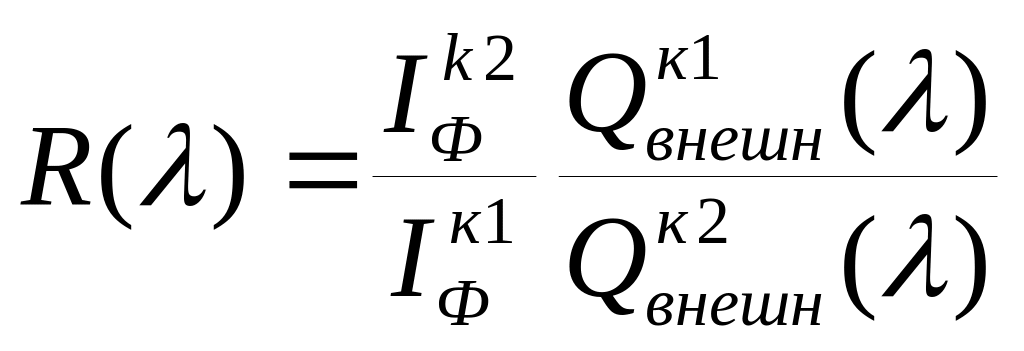(2.20) ,

где и - фототоки контрольных фотоприемников в темноте. На следующей длине волны процедура измерений и расчетов повторяется.

Рис. 2.4. Оптическая схема блока образцов при измерении спектральной зависимости коэффициента отражения

При измерении спектров коэффициента пропускания используется оптическая схема, аналогичная представленной выше. Однако, в этом случае исследуемый образец устанавливается в световом потоке, направляемом на второй контрольный фотоприемник (рис.2.5).

По результатам измерения фототоков контрольных фотоприемников и производится расчет коэффициента пропускания:

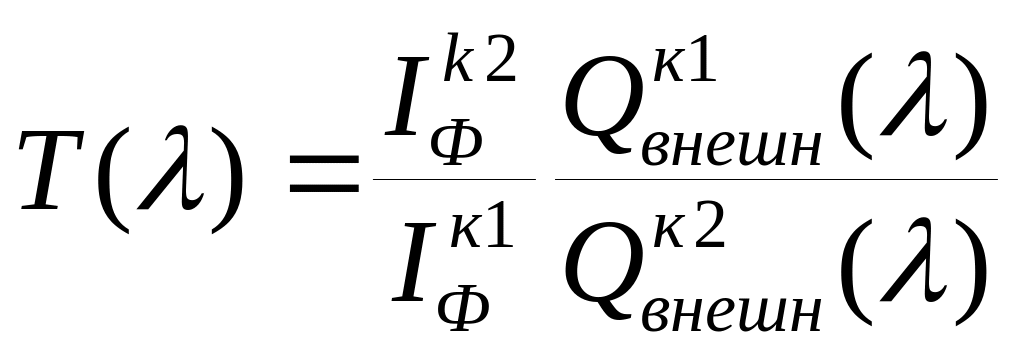(2.21).

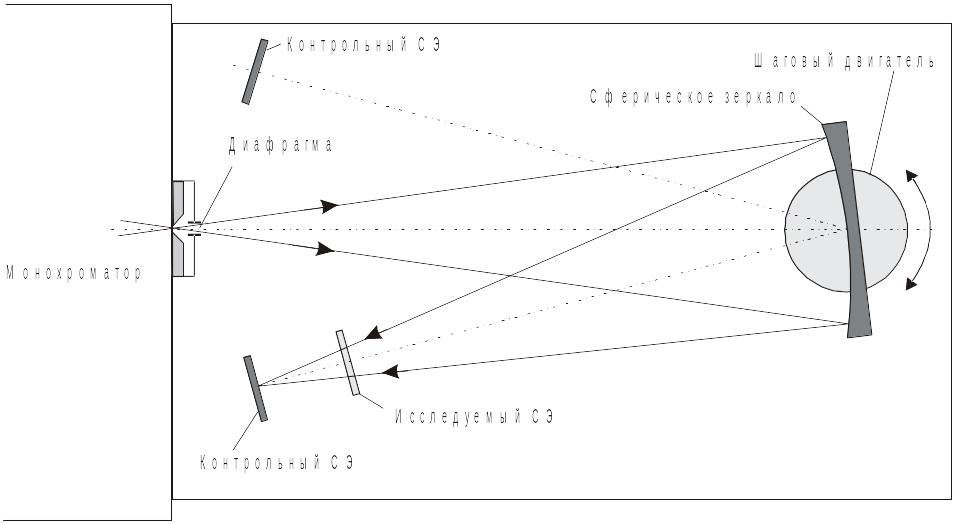
Рис. 2.5. Оптическая схема блока образцов при измерении спектральной зависимости коэффициента пропускания.

При использовании второго способа используется источник немонохроматического излучения, которое попадает на поверхность измеряемого образца. Оптическая схема реализации этого способа для измерения коэффициента отражения представлена на рис. 2.6, а для измерения коэффициента пропускания на рис. 2.7. Отраженное от поверхности образца (или прошедшее через образец, в случае измерения пропускания) поступает в спектрометр. Спектрометр производит измерение спектральной зависимости интенсивности излучения. Данный способ измерения спектров отражения требует проведения измерений на  контрольном образце с заведомо известным коэффициентом отражения во

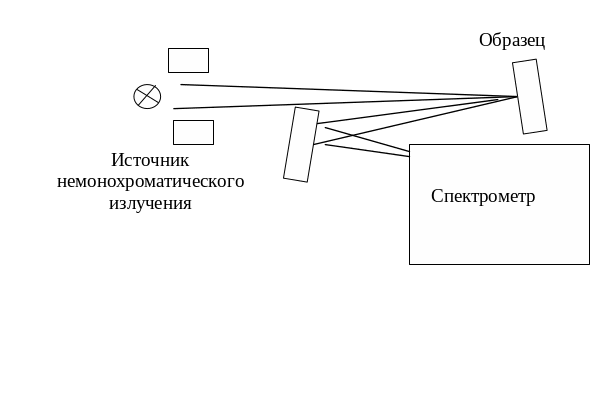
Рис. 2.6. Оптическая схема блока образцов при измерении спектральной зависимости коэффициента отражения.

Рис. 2.7. Оптическая схема блока образцов при измерении спектральной зависимости коэффициента пропускания.

всем измеряемом спектральном диапазоне R^эт(). Коэффициент отражения определяется следующим выражением:

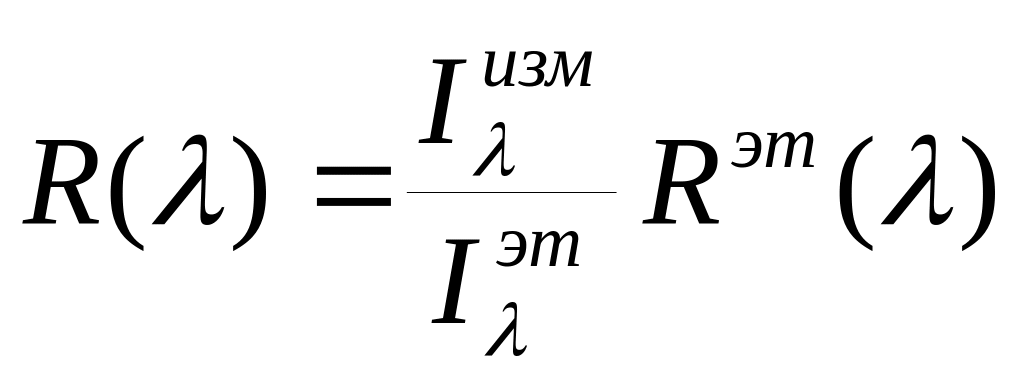(2.22),

где и - спектральные зависимости интенсивности сигнала от измеряемого и контрольного образцов, соответственно. Для измерения коэффициента пропускания достаточно провести измерение без образца. Коэффициент пропускания будет определяться следующим способом:

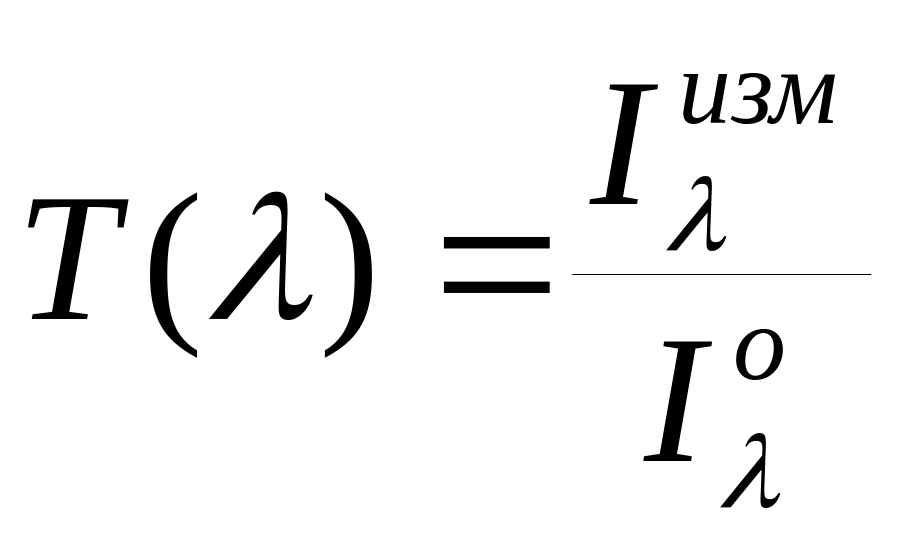(2.23),

где - спектральная зависимость интенсивности сигнала без образца.

В случае применения современных спектрометров, в конструкции которых используется комбинация дифракционной решетки и ПЭС матрицы, может быть достигнута очень высокая скорость измерения спектров, так как отсутствует необходимость вращения дифракционной решетки. Следовательно, второй способ измерения является наиболее оптимальным при организации методов экспресс диагностики.