
- •Реферат
- •Содержание
- •1.Расчет статически неопределимого стержня переменного сечения
- •2. Определение геометрических характеристик плоских сечений с горизонтальной осью симметрии
- •3. Расчет на прочность и жесткость статически определимой балки при изгибе
- •4. Расчет на прочность и жесткость статически определимой балки при изгибе.
- •5. Расчет на прочность и жесткость статически определимой балки при изгибе.
- •Список используемой литературы
Министерство образования РФ
Пензенский государственный университет
Кафедра техническая и прикладная механика
КУРСОВАЯ РАБОТА
По дисциплине: «Сопротивление материалов»
На тему: «Расчет на прочность и жесткость элементов конструкций»
Выполнил студент
Группы 09ММ2 Аминев Р.Р.
Руководитель Волчихина Н.И.
2010
Реферат
Пояснительная записка содержит 38 листов, 11 рисунков.
Ключевые слова: растяжение, сжатие, кручение, изгиб, моменты инерции, устойчивость, внешняя сила, внутренняя сила, напряжение, деформация, закон Гука.
Рассматриваемый объект: технические системы, загруженные внешними силами.
Цель работы: произвести расчет на прочность и жесткость элементов конструкций.
В процессе работы производился расчет на прочность и жесткость стержневых систем, работающих в условиях растяжения, сжатия, кручения, изгиба.
Содержание
Реферат……………………………………………………………………………2
Содержание……………………………………………………………………….3
Введение…………………………………………………………………………..4
1.Расчет статически неопределимого стержня переменного сечения…….......5
2.Определение геометрических характеристик плоских сечений с вертикальной осью симметрии…………………………………………………13
3. Расчет на прочность и жесткость статически определимой балки при изгибе………………………………………………………………………. ……19
4. Расчет на прочность и жесткость статически определимой балки при изгибе…………………………………………………………………………….28
5. Расчет на прочность и жесткость статически определимой балки при изгибе…………………………………………………………………………….33
Список используемой литературы……………………………………………..38
Введение
Сопротивление материалов — инженерная наука о методах расчета наиболее распространенных элементов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности и экономичности. Сопротивление материалов относится к фундаментальным дисциплинам общеинженерной подготовки специалистов с высшим техническим образованием.
В теоретической части сопротивление материалов базируется на математике и теоретической механике, в экспериментальной части — на физике и материаловедении и применяется при проектировании машин, приборов и конструкций. Практически все специальные дисциплины подготовки инженеров по разным специальностям содержат разделы курса сопротивления материалов, так как создание работоспособной новой техники невозможно без анализа и оценки ее прочности, жёсткости и надежности.
Задачей сопротивления материалов, как одного из разделов механики сплошной среды, является определение деформаций и напряжений в твёрдом упругом теле, которое подвергается силовому или тепловому воздействию.

1.Расчет статически неопределимого стержня переменного сечения
Расчет на прочность и жесткость статически неопределимого стержня переменного сечения при центральном растяжении и сжатии
Стержень имеет жесткое защемление по концам.
Цель: из условий прочности и жесткости подобрать безопасные диаметры жестко защемленного стального стержня переменного сечения, нагруженного сосредоточенными продольными силами (рисунок 1).
Рисунок 1 – Схема стержня переменного сечения, жестко защемлен по концам
Данные:
Материал стержня |
|
|
|
E, МПа |
nT |
nB |
Сталь Ст.3 |
3·10-4 |
210 |
380 |
2·105 |
1,5 |
2,5 |
P1 |
P2 |
P3 |
|
|
|
L1 |
L2 |
L3 |
L4 |
кН |
м |
||||||||
8 |
7 |
5 |
0,4 |
0,9 |
1,2 |
0,5 |
0,4 |
0,5 |
0,5 |
Порядок выполнения
Вычертить в масштабе расчётную схему с указанием активных и реактивных внешних сил.
Составить уравнение статики. Определить степень статической неопределимости (СНН).
Определить приведённые внутренние усилия
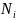 в пределах каждого участка.
в пределах каждого участка.Составить уравнение совместности .
Раскрыть статическую неопределимость стержня, решив совместно уравнение статики и уравнение совместности деформации.
Вычислить нормальные силы и построить их эпюру.
Выполнить проверку правильности вычислений.
Вычислить приведённый диаметр стержня по условию прочности и жёсткости.
Вычислить площадь
 поперечного сечения на каждом участке
стержня.
поперечного сечения на каждом участке
стержня.Определить действительные напряжения
 и построить их эпюру.
и построить их эпюру.Вычислить величину продольной деформации ∆
 на каждом участке.
на каждом участке.Определить перемещения сечений на границах участков вдоль оси Z и построить эпюру перемещений.
Сделать выводы.

 Составляю
уравнения статики. Определяю степень
статической неопределимости (ССН)
стержня.
Составляю
уравнения статики. Определяю степень
статической неопределимости (ССН)
стержня.

 (1)
(1)
Получено одно уравнение с двумя неизвестными RA и RB. Лишнее неизвестное указывает на статическую неопределимость стержня.
Степень статической неопределимости определяется как разность между количеством неизвестных nн и количеством возможных уравнений ny. В моей задаче nн=2, ny=1.
ССН=1, т.е. система один раз статически неопределима.
Записываю уравнения равновесия отсеченных частей стержня
Сечение:
на
1 участке 
на
2 участке 
на
3 участке 
на
3 участке 
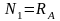 (2)
(2)
 (3)
(3)
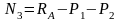 (4)
(4)
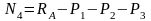 (5)
(5)
Составляю уравнение совместности деформаций.
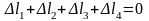 (6)
(6)
Выразил
деформации через внутренние усилия по
закону Гука -
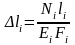 ,
поэтому для стержня, изготовленного из
одного материала, Ei
можно
обозначить через постоянную Е.
,
поэтому для стержня, изготовленного из
одного материала, Ei
можно
обозначить через постоянную Е.
 (7)
(7)
 В
данном уравнении делаю замену усилий
Ni
на соответствующие выражения:
В
данном уравнении делаю замену усилий
Ni
на соответствующие выражения:
 (8)
(8)
Раскрываю статическую неопределимость стержня, решая уравнения (1) и (8).
Подставляю в (8) все известные величины, нахожу RA.

RA=11,202 кН
Подставив найденное значение в (1) нахожу RB.
-11,202+8+7+5-RB=0
RB=8,798 кН
Вычисляю нормальные внутренние силы Ni.
N1=11,202 кН
N2=3,202 кН
N3=-3,798 кН
N4=-8,798 кН
Строю эпюру Ni (рисунок 2)
Делаю проверку вычислений.
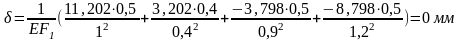
Результат проверки подтверждает правильность раскрытия статической неопределимости.
Вычисляю приведенные нормальные напряжения
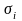 .
.

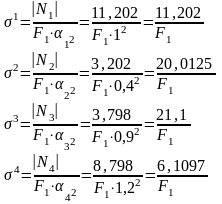
По приведенным напряжениям видно, что опасный участок – третий, так как
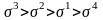
Из условия прочности и жесткости определяю приведенный диаметр сечения

Где d1 – приведенный диаметр.
Сначала вычисляю допускаемое нормальное напряжение.
Используя коэффициент запаса прочности по текучести, получаю:

Так же получаю коэффициент запаса прочности по временному сопротивлению:
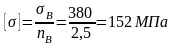
Из двух данных допускаемых напряжений принимаю наименьшее

 Определяю
диаметр d1
из условия прочности.
Определяю
диаметр d1
из условия прочности.
Условие прочности стержня

Так
как
 ,
то
,
то


Принимаю dпрочн=14 мм
Определяю диаметр d1 из условия жесткости
По
закону Гука
 ,
или
,
или
 .
.
Условие
жесткости
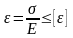 ;
;
 ,
,
Тогда

Из найденных по условиям жесткости и прочности диаметров я выбираю наибольший d1=21 мм
Далее определяю площади Fi сечений стержня по участкам.

Затем определяю действительные напряжения на участках и строю их эпюры (рисунок 2).
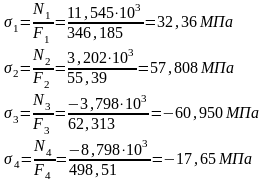
Нахожу величину продольной деформации
 на каждом участке
на каждом участке

И в заключении нахожу перемещения сечений A, C, D, E, B:
 ,
так как сечение А имеет жесткую заделку;
,
так как сечение А имеет жесткую заделку;
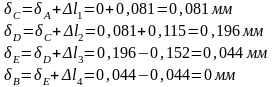
Строю эпюру перемещений сечений A, C, D, E, B (рисунок 2).
Вывод: последовательность вычислений перемещений сечений A, C, D, E и равенство нулю перемещения точки B указывают на правильность раскрытия статической неопределимости и правильность решения задачи по определению напряжений, деформаций и безопасных размеров поперечных сечений стержня.
 Принятые
в результате расчета размеры диаметров
поперечных сечений стержня обеспечат
его работоспособность, так как
удовлетворяют условиям прочности и
жесткости.
Принятые
в результате расчета размеры диаметров
поперечных сечений стержня обеспечат
его работоспособность, так как
удовлетворяют условиям прочности и
жесткости.

 ,
МПа
,
МПа ,
МПа
,
МПа


