Компьютерные технологии 2012/2013

Лабораторная работа № 6

Вариант № 1

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица 1

2.4	3.526	3.6	4.222
2.6	3.782	3.8	4.331
2.8	3.945	4.0	4.507
3.0	4.043	4.2	4.775
3.2	4.104	4.4	5.159
3.4	4.155	4.6	5.683

1. ;

2. ;

3. ;

4. ,

где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.

Лабораторная работа № 6

Вариант № 2

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица

1.5	10.517	4.5	8.442
2.0	10.193	5.0	8.482
2.5	9.807	5.5	8.862
3.0	9.387	6.0	9.701
3.5	8.977	6.5	11.132
4.0	8.637	7.0	13.302

1. ;

2. 

3. 

4. ,

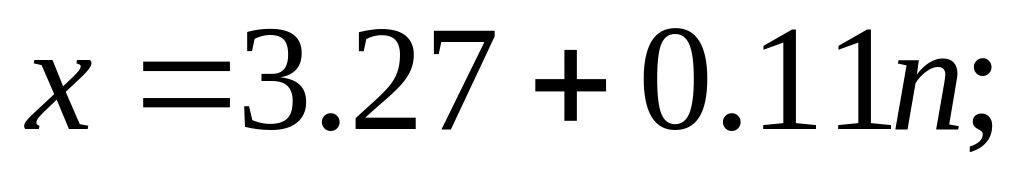
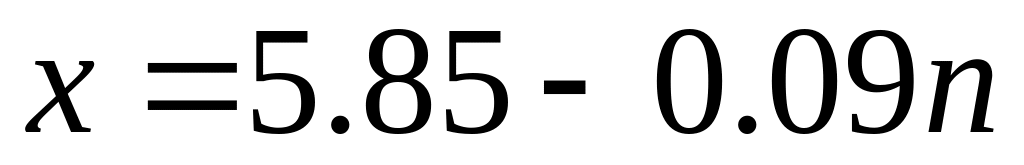где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.

Лабораторная работа № 6

Вариант № 3

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица 1

2.4	3.526	3.6	4.222
2.6	3.782	3.8	4.331
2.8	3.945	4.0	4.507
3.0	4.043	4.2	4.775
3.2	4.104	4.4	5.159
3.4	4.155	4.6	5.683

1. ;

2. ;

3. ;

4. ,

где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.

Лабораторная работа № 6

Вариант № 4

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица

1.5	10.517	4.5	8.442
2.0	10.193	5.0	8.482
2.5	9.807	5.5	8.862
3.0	9.387	6.0	9.701
3.5	8.977	6.5	11.132
4.0	8.637	7.0	13.302

1. ;

4. ,

где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

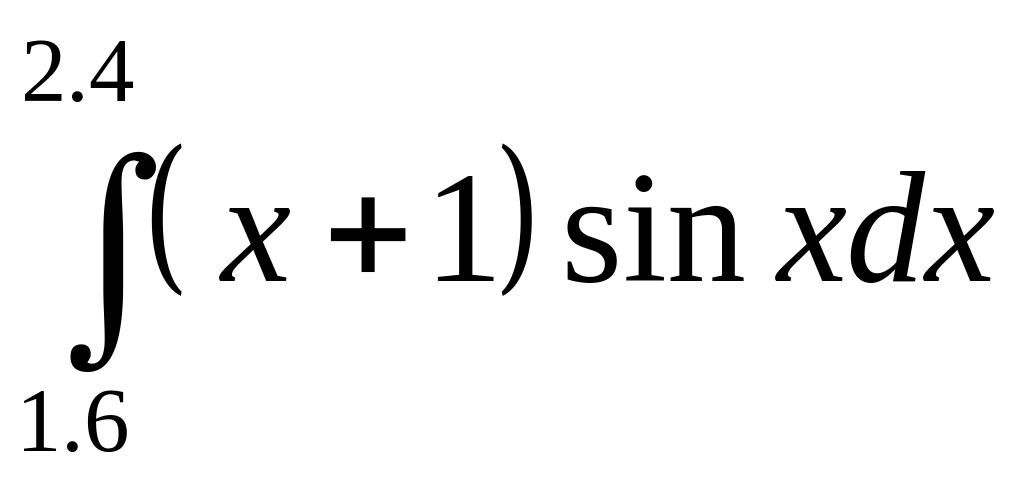2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.

Лабораторная работа № 6

Вариант № 5

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица 1

2.4	3.526	3.6	4.222
2.6	3.782	3.8	4.331
2.8	3.945	4.0	4.507
3.0	4.043	4.2	4.775
3.2	4.104	4.4	5.159
3.4	4.155	4.6	5.683

1. ;

2. ;

3. ;

4. ,

где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.

Лабораторная работа № 6

Вариант № 6

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица

1.5	10.517	4.5	8.442
2.0	10.193	5.0	8.482
2.5	9.807	5.5	8.862
3.0	9.387	6.0	9.701
3.5	8.977	6.5	11.132
4.0	8.637	7.0	13.302

1. ;

4. ,

где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.

Лабораторная работа № 6

Вариант № 7

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица 1

2.4	3.526	3.6	4.222
2.6	3.782	3.8	4.331
2.8	3.945	4.0	4.507
3.0	4.043	4.2	4.775
3.2	4.104	4.4	5.159
3.4	4.155	4.6	5.683

1. ;

2. ;

3. ;

4. ,

где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.

Лабораторная работа № 6

Вариант № 8

1. С помощью интерполяционной формулы Ньютона найти значение первой и второй производных при данных значениях аргумента для функции, заданной таблично.

Таблица

1.5	10.517	4.5	8.442
2.0	10.193	5.0	8.482
2.5	9.807	5.5	8.862
3.0	9.387	6.0	9.701
3.5	8.977	6.5	11.132
4.0	8.637	7.0	13.302

1. ;

4. ,

где − номер варианта.

2. Вычислить интеграл по формуле трапеций с точностью до трех знаков после запятой

.

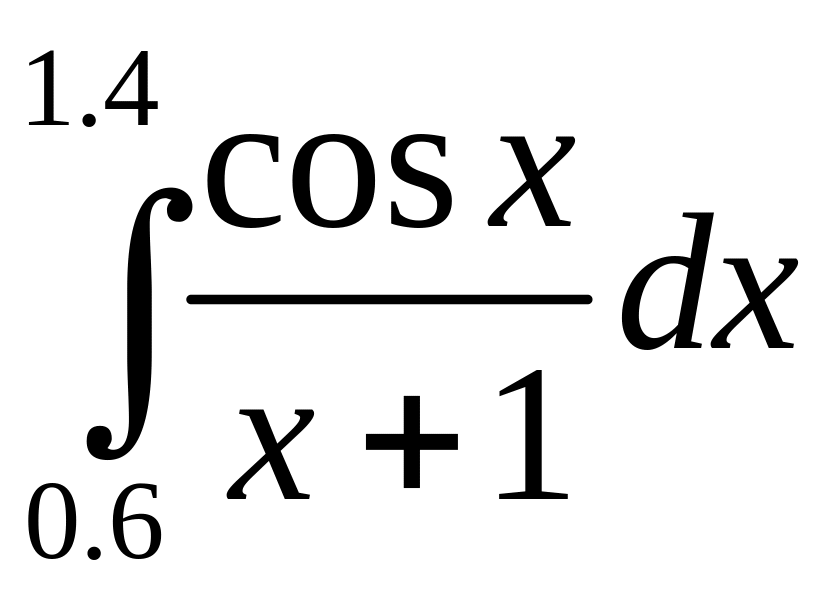2а) Вычислить интеграл, используя алгоритм квадратурных формул.

3. Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка на отрезке с шагом 0.1 при начальном условии . Все вычисления выполнять с четырьмя десятичными знаками.

.