"Разветвленная цепь постоянного тока".

1. Написать по законам Кирхгофа систему уравнений для определения токов в ветвях схемы и решить ее на ЭВМ.

2. Определить токи в ветвях схемы методом контурных токов и узловых потенциалов.

3. Составить баланс мощностей для исходной схемы.

4. Определить напряжения, измеряемые вольтметрами.

5. . Методом эквивалентного генератора определить ток во второй ветви (где E₂ и R₂ ), а также найти величину и напряжение ЭДС, которую надо дополнительно включить в эту же ветвь, чтобы ток в ней увеличился в два раза и изменил свое направление.

6. Создать модель заданной цепи в системе схемотехнического моделирования Micro-Cap. Запустить анализ цепи в режиме Transient. Сравнить полученные результаты с п. 1.

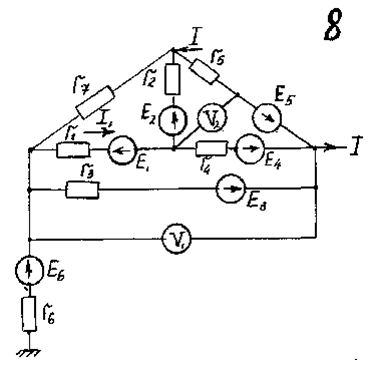
Числовые значения параметров схемы:

Для всех схем ток источника тока J = 4 А.

№ варианта в схемы № В^ул-аи-ль-

R1

R2

R3

R4

R5

R6

R7

E1

E2

E3

E4

E5

E6

E7

Ом

Ом

Ом

Ом

Ом

Ом

Ом

B

В

В

В

В

В

В

9

5

4

4

5

3

6

4

6

30

50

40

60

20

20

Выполнение расчета

1. Определение токов в ветвях методом уравнений Кирхгофа

Рассчитаем электрическую цепь, схема которой приведена задании.

Цепь содержит четыре узла (у=4) и шесть ветвей (b=6). Ветви с вольтметрами не учитываются, так как они имеют сопротивления, которые при теоретическом расчете токораспределения считаются бесконечно большими.

По законам Кирхгофа составим систему уравнений и решим их на ЭВМ.

Изобразим расчетную схему цепи (рис.1), на которой показываем произвольно выбранные положительные направления токов в ветвях, а также направления обхода контуров. Обозначим узлы цепи буквами A,B,С

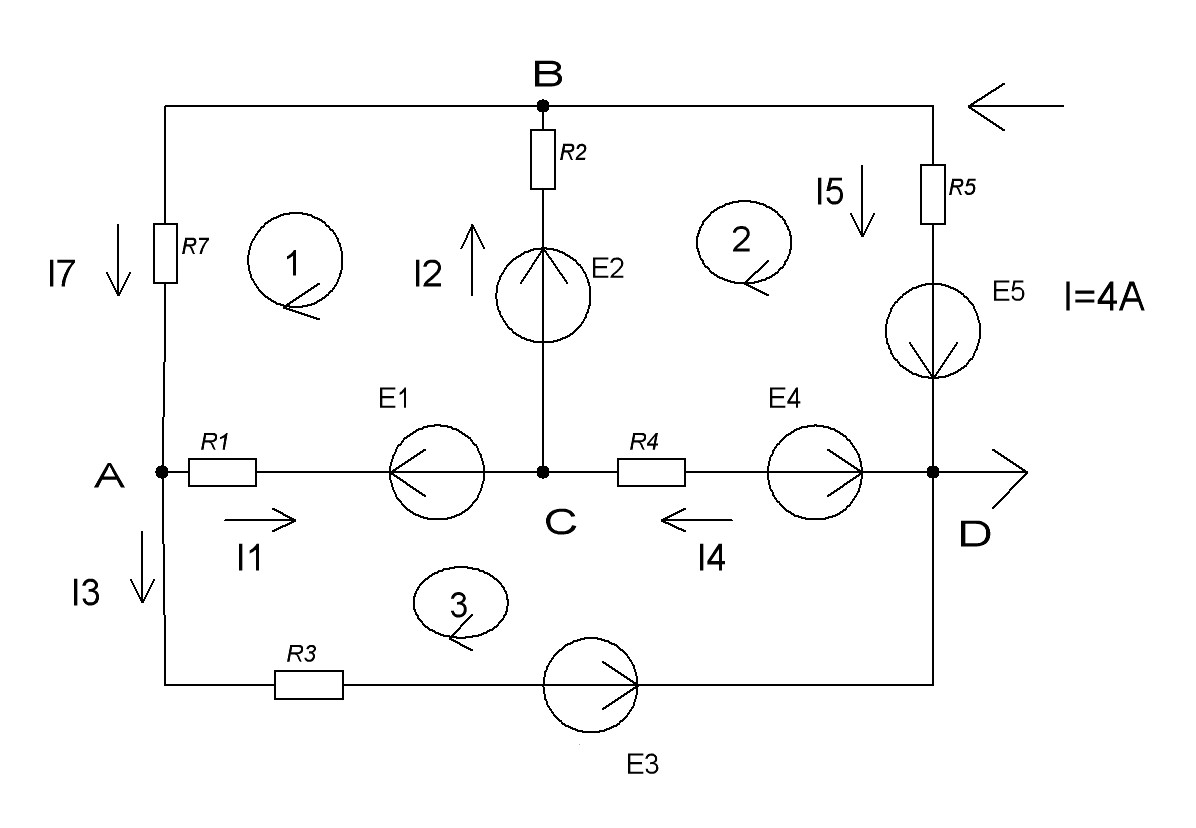Рис1.

По первому закону Кирхгофа можно составить 3 независимых уравнения. Положительными считаем токи, направленные к узлу.

Записываем эти уравнения для узлов A, B, C.

Узел A I1+I7+I3=0

Узел B -I2+I5-I7-J1=0

Узел C -I1+I4+I2=0

По второму закону Кирхгофа можно составить уравнения для трех независимых контуров.

Падение напряжения в сопротивлении считается положительным при условии, если направление тока в нем совпадает с произвольно выбранным направлением обхода контура, ЭДС источника считается положительной в том случае, если ее направление совпадает с направлением обхода контура.

Контур, для которого составляется уравнение по второму закону Кирхгофа, должен быть независимым, т.е. отличаться от предыдущих хотя бы одной новой ветвью.

Запишем уравнения по второму закону Кирхгофа:

Для контура I: I7·R7-I2·R2-I1·R1=-E2+E1

Для контура I I: -I4·R4+I2·R2+I5·R5=-E4+E2+E5

Для контура I I I: I3·R3-I4·R4-I1·R1=E3-E4+E1

Подставив в данные уравнения значения сопротивлений и ЭДС, получим следующие шесть уравнений:

I1+I7+I3-I6=0

-I1+I4+I2=0

-I2+I5-I7=4

-5I1-4I2+4I7=-24

-5I1-5I4+4I3=16

-5I4+4I2+3I5=50

Сформируем матрицу для решения данной системы уравнений при помощи доступных программных средств ЭВМ:

1 0 1 0 0 -1 1 | 0

-1 1 0 1 0 0 0 |0

0 -1 0 0 1 0 -1 |4

-5 -4 4 0 0 0 4 |-24

-5 0 4 -5 0 0 0 |16

0 4 0 -5 3 0 0 |50

В результате решения (программа rgr1.exe) получили:

I1=0,620 [A]

I2=3,785[A]

I3=0,819[A]

I4=-3,165[A]

I5=6,345[A]

I6=0,000[A]

I7=-1,440[A]