4. Силовой анализ механизма.

4.1. Определяем внешние силы, действующие на звенья 2,3 структурной группы.

Силы тяжести

Силы инерции

Момент пар сил инерции

4.2. В масштабе вычерчиваем структурную группу 2,3 в заданном положении и расставляем силы, действующие на звенья группы.

Сила полезного сопротивления Pc всегда направлена вдоль направляющей противоположно скорости точки С. Сила инерции P_И2 направлена параллельно вектору P_aS₂, но в противоположную сторону. Сила инерции

P_И3 направлена параллельно вектору P_aс плана ускорений, но в противоположную сторону. Чтобы найти направление , вектор nc переносим параллельно самому себе, упирая стрелкой с в точку С звена ВС. Этот вектор вращает точку С относительно точки В по(против) часовой стрелке - это направление . Момент пар сил инерции М_И2 направлен противоположно угловому ускорению . Сила R_O3 направлена перпендикулярно направляющей. В кинематической паре В приложены реакции отброшенных звеньев. Эти реакции неизвестны, поэтому представим их в виде составляющих, одна из которых направлена вдоль звена - нормальная составляющая R₁₂ⁿ и вторая - перпендикулярно звену - тангенциальная составляющая .

4.3. Запишем условие равновесия группы (2,3).

Составим уравнение моментов относительно точки С для звена 2, уравнение равновесия имеет вид

Находим

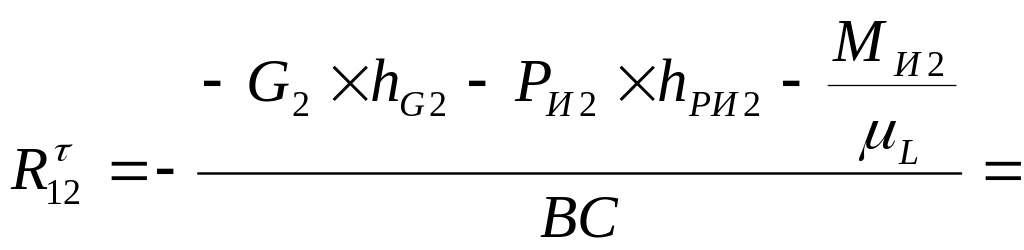
где ВС- длина звена 2, измеренная в мм на чертеже группы,

h_PИ2 - плечо силы P_И2 относительно точки С, это перпендикуляр, опущенный из точки С на линию действия силы P_И2 (измеряется в мм).

h_G2 - плечо силы G₂ в мм.

4.4. Решаем графически уравнение равновесия группы 2, 3. Выбираем масштаб плана сил

Вычисляем длины векторов, которыми будут изображаться силы на плане сил в масштабе

мм , мм , мм , мм , мм , мм.

4.5. Построение плана сил

Проводим линию действия силы - прямую параллельную ВС. В произвольной точке прямой откладываем вектор силы = мм перпендикулярно этой прямой. Из конца вектора откладываем вектор G₂ равный мм и т.д. в соответствии с векторным уравнением равновесия, т.е. складываем векторы геометрически.

4.6. Определяем реакцию в средней кинематической паре С.

Условие равновесия звена 2 имеет вид:

Соединяя конец вектора P_И2 и начало вектора , получаем реакцию в средней кинематической паре .

По плану сил определяем реакции.

R ₁₂=|R₁₂ |· µ_p= R₀₃=|R₀₃ |·µ_p=

R₃₂= |R₃₂ |·µ_p=

4.7. Силовой анализ механизма 1 класса.

С троим план кривошипа AB в масштабе. Прикладываем в точку В реакцию R₂₁=- R₁₂, перенося ее с плана сил группы звеньев, предварительно поменяв ее направление на противоположное. Прикладываем в точку В уравновешивающую силу Р_y AB. Составляем сумму моментов сил относительно точки А, определяем:

P_y= =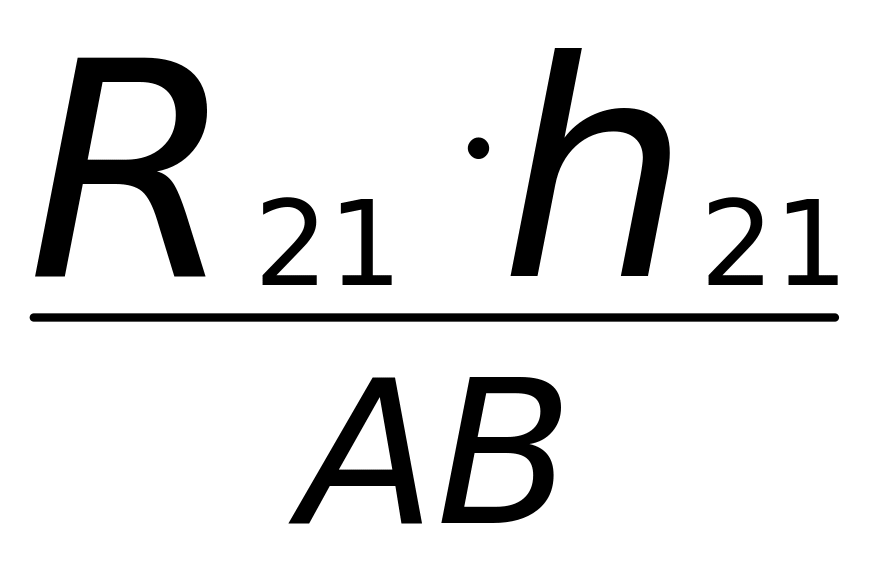

где h₂₁= мм – плечо реакции R₂₁.

По условию равновесия звена 1:

R ₂₁+ P_y+ R₀₁=0 строим план сил в масштабе µ_p= .

По построению определяем:

R ₀₁=|R₀₁|·µ_p=

4.8. Определяем потребную мощность двигателя

N=P_y·V_B=

5. Расчет передаточного отношения многозвенной зубчатой передачи.

5.1. Определяем число зубьев одного из колес из условия соосности их геометрических осей.

Для соосной передачи с двумя внешними зацеплениями колес a, b, c, d условие соостности представляется как

Z_a + Z_b = Z_c + Z_d.

Для заданной передачи это условие записываем как (проставить номера колес)

Z + Z = Z + Z ,

откуда определяем неизвестное число зубьев колеса (проставить номера колес)

Z = Z + Z - Z =

=

5.2. Находим передаточное отношение U₁₉ как произведение передаточных отношений ступеней (передач парой зацепляющихся колес, номера которых проставляем в следующем выражении)

U₁₉ = U₁₂ · U · U · U · U =

= · =

=

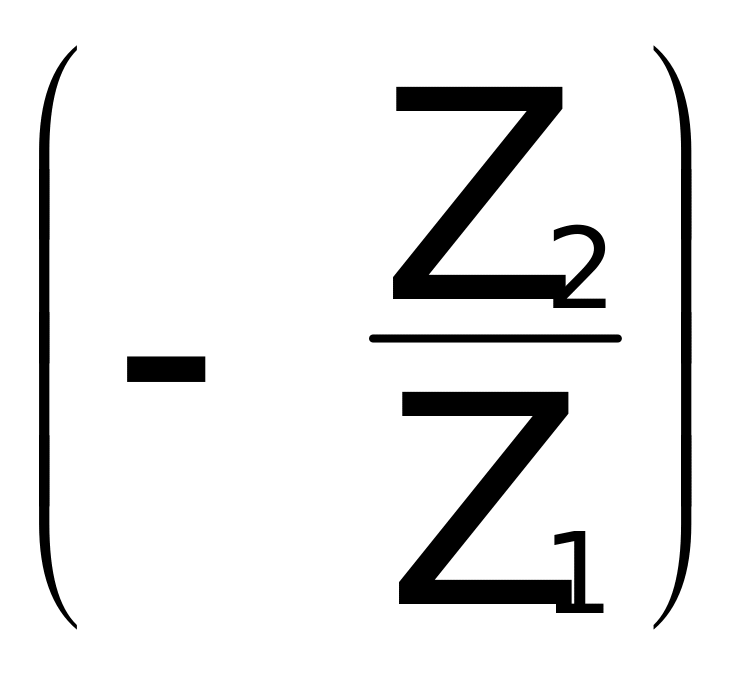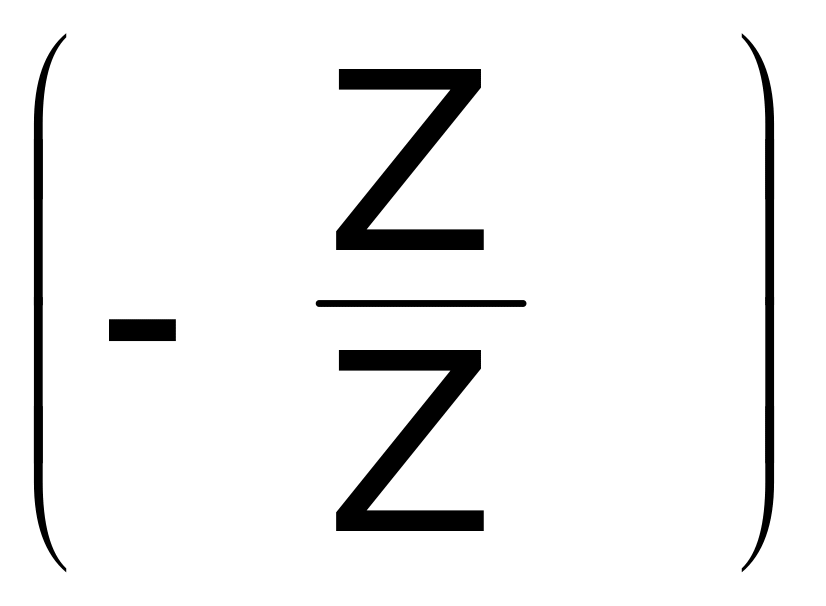5.3. Определяем диаметры начальных окружностей колес по формуле:

d_i=m·Z_i, где m=2мм – модуль зацепления колеса, Z_i – число зубьев колеса.

d ₁= mZ₁ = 2· = мм; d₂ = mZ₂ = 2· = мм; …..............

5.4. Строим схему зубчатой передачи в масштабе М 1:1.