1.3.1.2.Определение допускаемых напряжений.
а) допускаемые контактные напряжения определяются по формуле [1, стр.89]:
г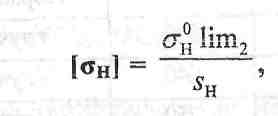
де
[БH2]
lim2 - предел выносливости на
контактную прочность материала зубчатого
колеса 2;
Sh - запас прочности.
Для сталей твердостью HB2< 350 БH0 и SH определяются по табл.7 (первая строчка).
б) допускаемые напряжения на изгиб определяются по формуле:
г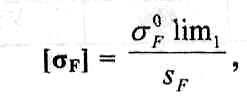
де
[БF1]
lim1 - предел выносливости на
контактную прочность материала зубчатого
колеса 1; SF - запас прочности.
БF0 и SF определяют по табл.7.
Таблица 6 Таблица 7 в приложениях
1.3.1.3.Определение расчетной нагрузки.
а) для первого зацепления при расчете на контактную прочность расчетный кру-тятттий момент:
г
де
КНд - коэффициент долговечности.
При проектировочном расчете можно
принять Кнд<1, [1, стр. 79].
КНа - коэффициент распределения нагрузки между зубьями. Для прямозубых колес КНа= 1 , [Метод, стр. 23].
КНB - коэффициент концентрации напряжений [Метод, стр. 23]. Кцр>1,05.
KHv - коэффициент динамической нагрузки [табл. 8.3].
б) при расчете на изгиб определяется расчетное окружное усилие:
в) для второго зацепления:
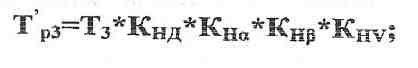
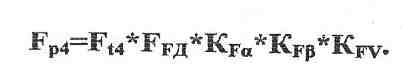
Необходимо учесть изменения скорости и, соответственно, коэффициенты KFa, KFV KFa KFV - Ориентировочные скорости определяются по формулам.
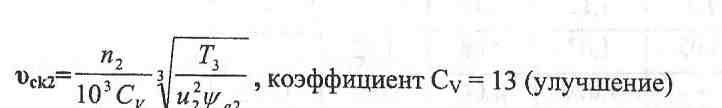
Таблица 8.2
Таблица8.3
Таблица 8.4
Примечание: В числителе приведены данные для прямозубых колес, в знаменателе - для косозубых. ■*
1.3.1.4.Расчет на контактную прочность.
При твердости зубьев НВ<350 расчет на контактную прочность проектировочный. Межосевые расстояния определяются по формулам [1,стр.98]:
где К=315 - для прямозубых колес; Ψa1 и Ψa2 - коэффициенты ширины колеса, рекомендуется выбрать из ряда;052; 0,25; 0,315: 0,355; 0,4; 0,5; 0,63.
Расчетные значения межосевых расстояний a'1 и а'2 округляются до ближайших значений из единого стандартного ряда: 40; 45; 50; 56; 63; 71; 80; 90; 100; 112; 125; 140; 160; 180; 200; 224; 250; 280; 315; 355; 400; 450; 500 и т.д.
Затем определяют модули зацеплений:
Е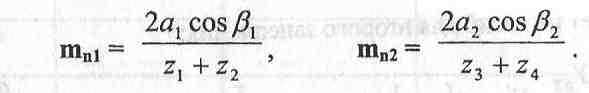
сли
колеса прямозубые, то cosB в формуле нет;
можно принимать z1=z2=(18-...24),
z2=z1*u1 и z4=z3*
u2.
Модули применяются по ГОСТу. Рекомендуемые значения модулей: 0,5; 0,6; 0,8; 1,0; 1,25; 1,6; 2,0;2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0 и т.д.
1.3.1.5.Расчет на изгиб.
Расчет на изгиб проверочный по формулам (для первого зацепления)
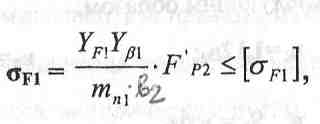
где YF1 - коэффициент формы зуба [1, стр.101] определяется в зависимости от эквивалентного числа зубьев (для косозубых колес):
Для прямозубых колес zэкв1=z1, YF1 выбирается для стандартных колес со смещением инструмента х=0:
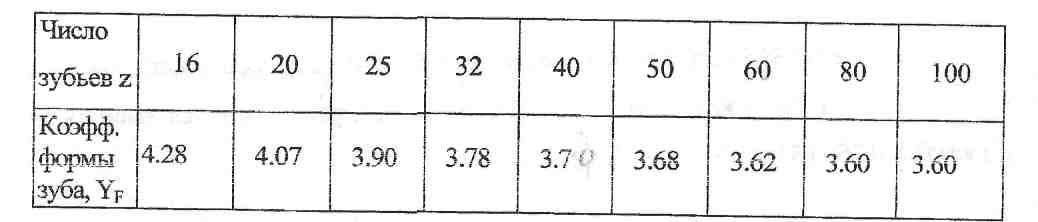
YB1 - коэффициент, зависящий от наклона зубьев:
Для прямозубых колес YB1=l.
Проверочный расчет на изгиб для второго зацепления:
1.3.1.6.О
пределение
основных параметров.
Диаметр делительный: d =mz/cosB , для прямозубых - cosB = 1.
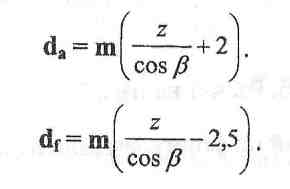
Диаметр выступов:
Диаметр впадин:
Ширина зубчатых колес определяется следующим образом:
Ш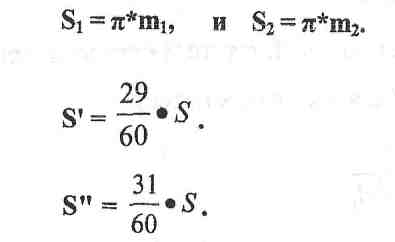
аг
зацепления:
Толщина зуба:
Ширина впадины:
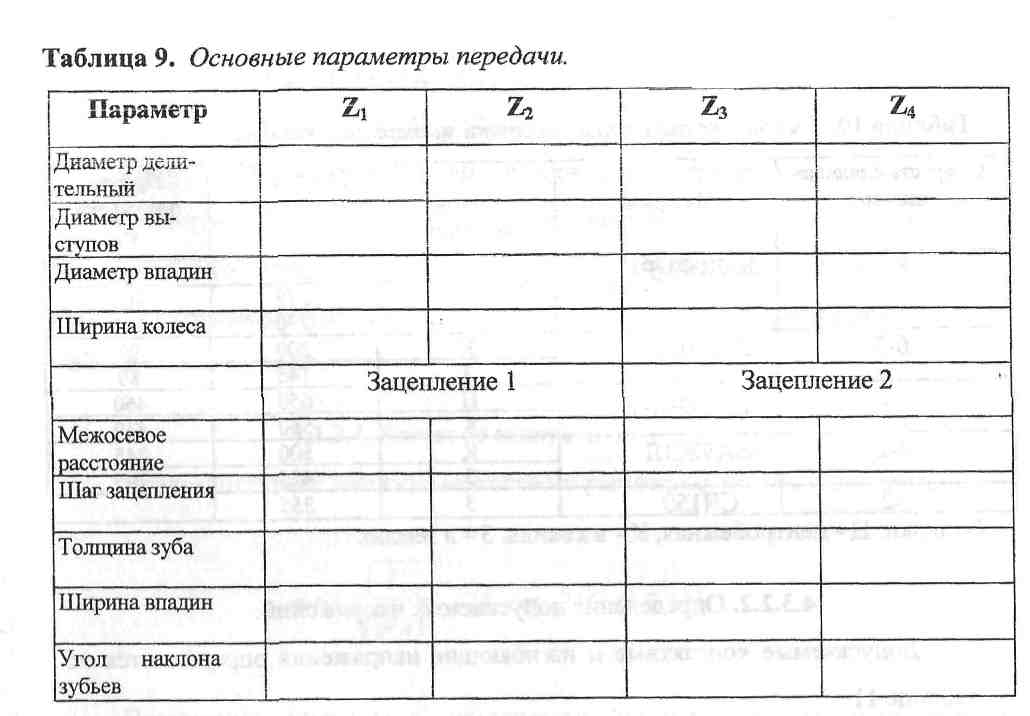
Результаты расчетов сводятся в
таблицу (табл.9)
1.4.Расчет валов.
1.4.1.Расчет валов цилиндрических редукторов.
1.4.1.1.Определение нагрузки валов цилиндрических редукторов.
Необходимо уточнить схему редуктора согласно технического задания. Цилиндрические двухступенчатые редукторы выполняются по развернутой, соосной или раздвоенной схеме [1, стр. 35-38]. Могут иметь горизонтальное или вертикальное исполнение (редкий случай - наклонное).
В цилиндрических прямозубых передачах полное усилие в зацеплении раскладывают на две составляющие: окружную и радиальную (распорную):
Таблица 14
В
цилиндрических косозубых передачах
полное усилие в зацеплении раскладывают
на три взаимно перпендикулярные
составляющие: окружную, радиальную и
осевую: