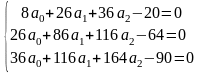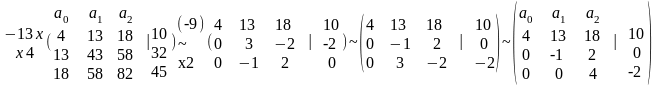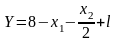Завдання № 20

1. Проаналізувати оцінку статистичної важливості параметрів моделей багатофакторної лінійної регресії та побудову для них інтервалів довіри.

Аналогічно до моделей ПЛР в моделях БЛР перевіряється статистична важливість параметрів з метою визначення, який із них, а отже і відповідний йому фактор, має важливе значення при оцінці впливу на показник, та будуються для параметрів інтервали довіри з метою встановлення числових меж можливих значень параметрів одержаних при розрахунках.

Перевірку важливості та побудову інтервалів здійснюють на основі t -статистики з певною ймовірністю α, таким чином:

 перевірка статистичної важливості параметрів:

а) розрахунок фактичного значень t -статистики для кожного з параметрів

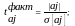
- середнє квадратичне відхилення параметру a_j,

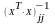– діагональний елемент матриці (X^T · X)^-1

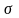- середнє квадратичне відхилення регресії

б) задати ймовірність α, з якою перевірятиметься статистична важливість, для неї та для числа к = n–m–1 знайти табличне значення t- статистики t ^табл. = t (α; k)

в) порівняти фактичне значення t- статистики з табличним і зробити відповідний висновок. А саме, якщо: вважати статистично неважливим з ймовірністю α; якщо ж 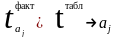вважати статистично важливим.

 Побудова для параметрів інтервалів довіри:

а) задати ймовірність α, з якою будуватимуться інтервали довіри, і для неї та числа k = n–m–1, знайти табличне значення t- статистики. t ^табл. = t (α; k).

б) знайти для кожного з параметрів моделі 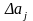= t ^табл · σ[a_j], – можлива похибка його значень.

в) побудувати інтервали довіри для кожного параметру, як інтервали вигляду

2. Порівняти методи побудови моделей парної і багатофакторної моделей регресії.

Парний регресійний аналіз – вид регресійного аналізу, що включає у себе розгляд однієї незалежної змінної величини, а багатофакторний – відповідно дві величини і більше.Зважаючи на характер зв'язку, в регресійному аналізі можуть використовуватися лінійні та нелінійні функції. Для визначення характеру залежності та, відповідно, побудови рівняння регресії доцільно застосувати графічний метод, порівняння рівнобіжних рядів вихідних даних, табличний метод.

Так, графічний метод дає найбільш наочну картину розміщення крапок на графіку, завдяки чому можна виявити напрям і вид залежності між досліджуваними показниками: прямолінійна чи криволінійна.

За допомогою порівняння рівнобіжних рядів ознак можна спостерігати за рівномірністю їх взаємних змін. Якщо зміна факторної ознаки (х) призводить до відносно рівномірної зміни результативної ( ), тоді використовується лінійна функція (наприклад, залежність між урожайністю культур і кількістю внесених добрив).

Найпростішим рівнянням парної регресії, що описує лінійну залежність між факторною і результативною ознаками, є рівняння прямої, яке має такий вигляд:

,

де   – залежна змінна, яка оцінюється або прогнозується (результативна ознака);

 – вільний член рівняння;

 – коефіцієнт регресії;

х – незалежна змінна (факторна ознака), яка використовується для визначення залежної змінної.

Метод регресійного аналізу вважається найдосконалішим з усіх використовуваних нині нормативно-параметричних методів. Він широко застосовується для аналізу та встановлення рівня і співвідношень вартості продукції, яка характеризується наявністю одного або декількох техніко-економічних параметрів, що характеризують головні споживчі якості. Регресивний аналіз надає можливість знайти емпіричну форму залежності ціни від техніко-економічних параметрів товарів і виробів. При цьому він виступає в ролі цільової функції параметрів.

Метод регресійного аналізу особливо ефективний за умови здійснення розрахунків за допомогою сучасних інформаційних технологій і систем.

На практиці економічний процес змінюється під впливом багатьох різноманітних факторів, які треба вміти виявити та оцінити. Якщо розглянути приклад з лк 30 , то аналіз обсягу продажу на фірмі було б спрощено допускати тільки від витрат на рекламу. На обсяги продажу впливає частина ринку, яку утримує фірма, якість продукції, імідж марки продукції, середня заробітна плата населення у регіонах продажу та інші фактори.

Узагальнена багатофакторна лінійна регресійна модель може бути записана у вигляді:

 (1)

де у – залежна змінна, х₁,  х₂,…х_p – незалежні змінні (фактори) а₀, …а_р – параметри моделі, які потрібно оцінити, e - не спостережувана випадкова величина.

Узагальнена регресійна модель – це модель, яка дійсна для всієї генеральної сукупності. Невідомі параметри узагальненої моделі є константами, а випадкова величина – не спостережувана, і можна лише зробити припущення відповідно до закону її розподілу. На відміну від узагальненої регресійної моделі, вибіркова модель будується для певної вибірки; невідомі параметри вибіркової моделі є випадковими величинами, математичне сподівання яких дорівнює параметрам узагальненої моделі.

Відповідна вибіркова лінійна багатофакторна модель має вигляд:

,        (2)

де ŷ – залежна змінна, х₁…х_р – незалежні змінні, b₀, b₁…b_р – оцінки невідомих параметрів узагальненої моделі, е – випадкова величина (помилка).

Нехай дано ряд спостережень за залежною змінною   та за незалежними змінними, або факторами:  . На підставі цих спостережень будується лінійна вибіркова багатофакторна модель, а саме – у вигляді (2).

В економетрії явище, яке залежить від багатьох факторів описують на основі моделей БР. Розрізняються лінійні та нелінійні моделі БР.

Моделлю БЛР називають модель, яка встановлює лінійну залежність більше, ніж 2-ома змінними, при цьому, одна із змінних – залежна (y /показник/) і розглядають як лін. функцію від m змінних – незалежних X₁, X₂, X₃, … , X_m , m ≥ 2 (фактори, що впливають на показник).

Загальний вигляд моделі:

Y= a₀ + a₁X₁ + a₂X₂ + … + a_m X_m + l (1)

В моделі (1):

Y-показник, вектор спостережень за залежною змінною

Y= (y₁, y₂,…,y _n)

X₁, X₂, X₃, … , X_m; - фактори, вектори спостережень за незалежними змінними

X₁=(x₁₁, x₁₂, x₁₃, …, x_1n)

X₂= (x₂₁, x₂₂, x₂₃, … , x_2n)

…

X _m=( x_m1, x_m2, x_m3, … ,x _mn)

a₀, a₁, a₂, … , a_m – невідомі параметри моделі, знаходження яких є основним завданням побудови моделей даного виду.

l – випадкова величина, вектор спостережень вигляду l=(l₁, l₂, … , l_n)

Моделі (1) аналогічно до моделей лінійної регресії розглядають як суму 2-ох складових:

 регресія ( = a₀ + a₁x₁ + a₂x₂ + … + a_mx_m ) характеризує середнє (розрахункове) значення показника для заданих значень фактора =a₀ + a₁x_1i + a₂x_2i + … + a_nx_ni

 відхилення l стат. даних показника від розрах. значень

L = Y – ( a₀ + a₁x₁ + a₂x₂ + … + a_mx_m) =

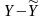
Відносно моделей (1) в економетрії вводяться ряд припущень, виконання яких є обов’язковим. Їх порушення призводить до певних негативних наслідків, тому кожне з припущень в економетрії вивчається і досліджується.

З вище викладеного, основним завданням побудови моделей багатофакторної лінійної регресії Y = a₀ + a₁X₁ + a₂X₂ + … + a_mX_m + l є знаходження їх параметрів a_0, a_1, a₂,…, a_{m .}

Аналогічно до моделей ПЛР з цією метою в моделях БР застосовують метод НК.

Суть методу полягає в тому, що невідомі параметри моделі знаходять таким чином, щоб сума квадратів відхилень стат. даних показника від його розрахункових значень була min

Іншими словами за методом НК для багатофакторних лінійних моделей параметри шукають, як точку min функції

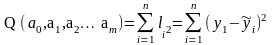
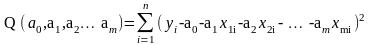
Аналогічно до моделей ПЛР в моделях БЛР цю точку знаходять застосовуючи:

 необхідну умову існування точки min функцій багатьох змінних (рівність 0 частинних похідних 1-го порядку функції 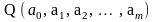по змінним a_0, a_1, a₂,…, a_{m ).}

 достатню умову існування min функції багатьох змінних (додатня визначеність визначника, складеного з частинних похідних 2-го порядку функції по змінним a_0, a_1, a₂,…, a_{m .}).

При застосуванні достатньої умови виникає складність, пов’язана з великим обсягом розрахунків при доведенні додатної визначеності визначника.

Тому у методі НК для моделей БЛР доведення достатньої умови опускають, припускаючи, що вона за відомо виконується, і даний метод зводиться до застосування тільки необхідної умови.

Отже, за методом НК при знаходженні невідомих параметрів моделей БЛР необхідно:

- побудувати функцію Q

- знайти частинні похідні 1-го порядку функції Q по змінним a_0, a_1, a₂,…, a_m

- прирівняти одержані похідні до 0 і об'єднати їх у систему

- розв’язати систему методом Гауса і розв’язок вважати min функції Q, а отже

і значеннями невідомих параметрів.

Приклад:

На основі статистики впливу 2-ох факторів на показник методом НК побудувати модель двофакторної ЛР

Y\X	X1	X2
3 3 2 2	3 3 3 4	4 5 5 4

1) будуємо розрахункові значення показника

2) будуємо відхилення

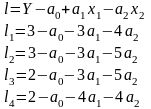
3) будуємо функцію, яка є Σ квадратів відхилень

4) Знаходимо частинні похідні 1-го порядку функції

=

=

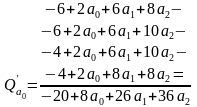
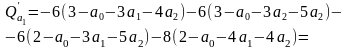
5) Прирівнюємо одержані похідні до 0, об’єднаємо в с-му і розв’язуємо методом Гауса