Тема 7.Нейроний класифікатор Хеммінга.

Нейроний класифікатор Хеммінга Такий класифікатор являє собою двошарову рекурентну мережу, структура якої пока­зана на рисунку 1.7 він бул запропонований Ліппманом. Кожний з двох шарів мережі Хеммінга створює підмережу з різною архітектурою; перший шар мережі — однонаправлений, з потоком сигналів від входу до виходу. Вхідна підмережа містить N нейронів та визначає відстань в змісті Хем­мінга між вхідним вектором и кожним класом, який був запам‘ятований. Відстань по Хеммінгу між двійковими векторами визначається числом позицій, на яких біти в вхідному зразковому векторі відрізняються від бітів в зразку, який був запам‘ятований для даного класу. Відзначимо, що для визначення відстані Хеммінга можна використовувати будь який відомий алгоритм. При цьому вхідні ваги є оцінкою по Хеммінгу для вхідного зразка: вони оцінюють, чи відповідає даний зразок еталону.

Рисунок 1.7

Вихідна підмережа, що називається МАХNЕТ, містить М виходів, що визначає число зразків які розпізнаються мережею. Ця рекуррентна мережа по архітектурі подібна мережі Хопфілда і є допоміжною. Її призначення — вибір класу, найбільше близького до вхідного зразка. МАXNЕТ подавлює всі вихідні сигнали, крім самого потужного в першому шарі. Дія нейромережної моделі Хеммінга як векторного класифікатора полягає в виборі мінімальної відстані по Хем­мінгу між двійковим вектором, що подається на вхід мережі, та векторами, що являють собою навчальні зразки, які закодовані в структурі мережі.

Дія нейроподібної моделі Хеммінга, як векторного класифікатора, полягає у виборі мінімальної відстані по Хеммінгу між двійковим вектором, що подається на вхід мережі та векторами, що являють собою навчальні зв'язки,закодовані в структурі мережі.

Для визначення основних величин класифікатора Хеммінга припустимо, що р-й вихідний сигнал дорівнює 1, тоді і тільки тоді, коли X=S^(P), тобто це означає, що на вхід буде поданий зразковий вектор класу р. В такому випадку синаптичні ваги перщого шару повинні бути заданими:

Звідси випливає, що якщо на вхід мережі надходить біполярний вектор, складові одиниці якого дорівнюють 1, то скалярний добуток векторів можна обчислити як різницю між числом позицій, на яких вектори рівні та на яких вони відрізняються. Як було відзначено вище, число позицій, на яких складові елементи векторів нерівні, визначає відстань Хеммінга R(х,S^P).

де X^T - транспонований вхідний вектор X.

Позначимо W_ij - вага з'єднання і-го входу з j-тим нейроном нижнього (вхідного) шару, де W - матриця ваг . Тоді з рівняння 1:

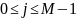
Таким чином, навчання вхідної підмережі класифікатора Хеммінга полягає в тому, що вона повинна запам'ятати величини усіх зразкових векторів у вхідних вагах:

де X^і_j – і-й компонент j-гo еталонного вхідного вектора.

Значення порогів нейронів вхідного шару задаються так: σ =n/2. Результуючий сигнал збудження нейронів мережі Хеммінга можна представити:

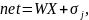
де WX — скалярний добуток матриці ваг та вхідного вектора.

Враховуючи (3.1) запишемо:

У вхідній підмережі приймаємо, що активаційна функція нейронів нелінійна. На рисунку 3.2 представлена активаційна функція нейронів першого шару підмережі Хеммінга. Вихідна величина j-гo нейрону вхідної підмережі подібності вхідного зразка j-му класу.

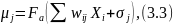
де µ_j - вихід j-гo нейрону вхідної шдмережі;

F_a – активаційна функція нейрона.

Вихідний сигнал кожного нейрону нормалізуємо в інтервалі {0,1}.

Рисунок 3.2 – Активаційна функція нейронів першого шару підмережі Хеммінга

Розраховані вихідні величини нейронів нижнього шару подаються потім на входи нейронів підмережі MAXNET, в якій існують зв'язки, що збуджують і гальмують. Збуджуючі зв'язки мають ваги рівні 1, інші ваги кожного нейрона мають ваги рівні -ε і є гальмуючими.

Т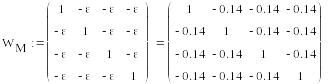 аким чином, ваги з'єднань верхнього вихідного шару встановлюються за наступним правилом:

де величина ε змінюється від 0 до 1/М. (0<ε<1/М).

Пороги нейронів у вихідній підмережі дорівнюють 0. Ваги з'єднань між нейронами вхідної та вихідної підмережі приймаються рівними 1. Інші зв'язки кожного нейрона мають ваги, що дорівнюють – ε . Припустимо, що вхідний ситная до вихідної шдмережі служить тільки до моменту ініціалізації ітерації, після чого стає неактивним. Приймемо, що ζ_i – вихід і-го нейрона вихідної шдмережі:

В вихідній підмережі приймаємо, що F(U_j) – активаційна функція нейронів, нелінійна, як на рис. 3.З, де представлена активна функція нейронів в підмережі MAXNET.

Рисунок 3.3 - Активна функція нейронів в підмережі MAXNET

Тоді ітерації у вихідній підмережі можна описати наступним правилом:

n+1 - чергова ітерація,

В роботі мережі можна виділити два етапи:

На вхід мережі подається N елементних векторів X. Час подачі повинен бути достатнім для того, щоб нейрони першого шару отримали визначені величини вихідних сигналів, що ініціалізують початковий стан другого шару. Матриця ваг між вхідним і нижнім шаром визначає добуток між кожним еталонним вектором і класом, заданим на вході,

На другому етапі мережа Хеммінга віддаляється і починається ітераційний процес, в другому шарі, заданий початковим станом на першому етапі, ітерації у вихідній підмережі продовжується до тих пір, поки всі нейрони не приймуть стан рівний нулю. Нейрон не з нулевим вихідним сигналом – переможець, представляє собою клас, до якого належить вхідний вектор.

Переваги:

велика стійкість до випадкових завад інформації;

простота архітектури, що дозволяє активізувати і підбирати параметри нейронної мережі;

при порівнянні з мережами, що навчаються за допомогою алгоритму зворотного поширення (Back Propagation), наприклад, з багатошаровим персептроном, в яких ініціалізація здійснюється випадковим чином, мережі Хеммінга переважаючі.

Алгоритм зворотного поширення, за своєю суттю, не більше ніж, локальний метод і не гарантує закінчення процесу навчання мережі в точці глобального екстремуму. Крім того, він для досягнення мінімуму заданої помилки (що використовується для оцінки якості штучної нейронної мережі вимагає дуже великого числа ітерацій, що і стало причиною різних модифікацій і розробок різних алгоритмів).

Доведено, що нейронна мережа Хеммінга завжди досягає стану стабілізації тільки з одним максимальним позитивним нейроном в вихідному шарі ε<1/М. Мережа Хеммінга діє паралельно , тому вона володіє високою швидкістю (швидкодією). Простота методу навчання мережі: синаптичні ваги задаються методом одноразового прийняття визначеного значення, а не в результаті навчання крок за кроком, що є типовим для настроювання (навчання) мережі без вчителя, таким чином класифікатор Хеммінга можна розглядати як самонастроювальну мережу, так як він користується такою ж

Принцип роботи алгоритму розпізнавання нейронного класифікатора Хеммінга

оцінкою подібності як і багато інших мереж. Обчислює скалярні добутки, визначаючи ступінь подібності класифікованого вектора, записаного в вигляді синаптичних ваг зразковим вектором, що представляє класи.

При порівнянні з мережами, перевагою є те, що вона вимагає значно меншого числа зв'язків між нейронами. Число це залежить від числа класів, що визначаються, а також від розмірності вхідного сигналу.

Наприклад, для 100 входів та 10 розпізнаних класів Хеммінга, потрібно 10000 з'єднань.

Крім того, мережа Хеммінга має великий недолік: обмеження ємності (що полягає в тому, що ця мережа може запам'ятати дуже маленьке число класів М=0,05 – число нейронів в мережі).

В мережі Хеммінга кожному запам'ятовуваному класу відповідає один нейрон у вхідній підмережі і один у вихідній, тобто вона містить в два рази більше нейронів, в порівнянні з числом запам'ятованих класів і тому її ємність = 1/М.