Тема 5. Мережа Хопфілда.

Структура нейронної мережі. Алгоритм навчання та розпізнавання образів. Формування матриці зв'язків.Переваги над іншими нейронними мережами. Поводження моделі повнозв'язної мережі бінарних нейроподібних елементів із симетричними зв'язками. Побудова алгоритму моделі Хопфілда засобами MathCad. Роботи, що проводяться для поліпшення характеристик моделі Хопфілда. Шляхи використання нейронного класифікатора Хопфілда для розпізнавання образів.

Мережа Хопфілда.

Хоча численні результати моделювання демонстрували стабільність ансамблевих мереж зі зворотними зв'язками і хеббівським правилом навчання (еволюцію мережі до стійкого стану), відсутність математичного обґрунтування такого поводження перешкоджало їхньої популярності. Положення змінилося з появою робіт, де було визначене підмножина нейроних мереж зі зворотними зв'язками, що гарантовано досягають стійкого стану.

У 1982 р. американський біофізик Джон Хопфілд опублікував статті, де на підставі аналогії між нейроними мережами й особливим класом фізичних систем — спіновими стеклами — йому вдалося залучити до аналізу нейромережних моделей могутній математичний апарат статистичної фізики. Це стимулювало вторгнення в область моделювання нейроних мереж великого загону вчених-фізиків, якими в даний час отримано багато цікавих аналітичних результатів.

Сам Хопфілд у згаданій статті розглянув поводження моделі повнозв’язної мережі бінарних нейроподібних елементів із симетричними зв'язками (wsj = Wji). Елементи функціонували в асинхронному режимі, тобто кожен нейрон у випадкові моменти часу з деякою середньою частотою визначав свій стан відповідно до правила (1.3). Це дозволило описати поводження мережі як релаксаційний процес, при якому мінімізується енергетична функція Е (функція Ляпунова, Гамільтона) моделі:

Е = — 1/2W_ij*y_i*y_j + _i*y_i;

^{ij i}

де W_ij — матриця зв’язків; y_i і _i — стан и поріг модельного нейрону. Дійсно, зміна Е при зміні стану нейрона

E = _i*w_ij*y_i;

Так як знак  y_i співпадає з знаком w_ij*y_i, очевидно, що Е в міру спрацьовування нейронів буде монотонно зменьшуватися, а тому що Е обмежена, буде досягнутий стан її мінімуму. Таким чином, еволюція мережі з будь-якого початкового стану приводить до стану, що відповідає локальному мінімуму Е. Можна провести анологію поводження мережі з рухом легкої частки по деякому грузлому рельєфові під дією сили ваги.

У роботі Хопфілд досліджував мережу з нейроподібними елементами, що мають сигмоїдну характеристику. Стан нейронів такої мережі змінюються одночасно і безперервно, і мережа описується системою диференціальних рівнянь. Хопфілд довів збіжність і такої мережі до стабільних енергетичних мінімумів і знайшов відповідність між її стійкими станами і стійкими станами мережі з бінарними елементами. Це послужило основою для побудови апаратних моделей, де мережа реалізується як аналогова електронна схема, що складається з операційних підсилювачів, що моделюють нейрони, з'єднаних резисторами з провідностями (рис. 1.5).

Зрозуміло, що якщо зробити мінімумами енергії заданий набір паттернів нейроної активності (образів), обидва варіанти мережі Хопфілда зможуть виконувати функції асоціативної пам'яті, «скочуючись» до того образа, у чий «басейн притягання» попадає початковий паттерн активності нейронів мережі. Наприклад, на рис. 1.6 показане відновлення мережею з 40 нейронів, що розташовані у виді матриці 5х8, запамятованого в мережі зображення букви «Ј». Активному нейрону відповідає заштрихований елемент зображення. З поданого на мережу зашумленого зображення (ліворуч) відновлюється правильне зображення (праворуч).

Я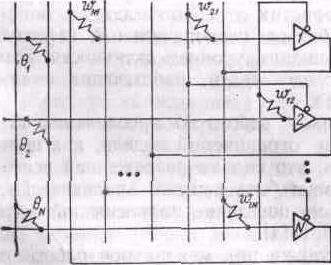 к і слідувало очікувати, одним зі способів одержання потрібної енергетичної функції є формування матриці зв'язків відповідно до варіанта хеббівського правила _L

w_ij = (2Z_i^p1)( 2Z_j^p1);

^p=1

д

Рисунок 1.5

е Z^p — образи, які треба запам'ятати в мережі; L — їхня кількість. Це правило, як і правило, запропоноване Хеббом, забезпечує формування симетричної матриці зв'язків, однак постулює збільшення ваги зв'язків між не тільки одночасно активними, але й одночасно неактивними нейронами, а також його зменшення між нейронами, що знаходяться в різному стані. Таке правило допускає існування гальмуючих зв'язків, що модифікуються, між нейронами і навіть перехід збудливих зв'язків у гальмуючі. Воно дозволяє мережі автоматично саморегулювати рівень

Рисунок 1.6

активності і працювати з нульовими порогами нейронів. Однак при цьому значно знижується ємність пам'яті мережі: кількість випадкових образів, яку можна записати в мережу з можливістю відновлення, не перевищує 0,14 кількості нейронів. Крім того, на додаток до енергетичних мінімумів, що відповідають запамятованим образам, виникають помилкові мінімуми функції Е. Положення ще більш ускладнюється для зкорельованих образів, що після запам'ятовування не стають мінімумами Е.

Одне з основних застосувань мережі даного типу – асоціативна пам’ять. У цьому випадку ваги зв’язків задаються один раз і вже не змінюються. Крім того мережі Хопфілда дозволяють вирішувати задачу класифікації і оптимізації.

Мережа Хопфілда – одношарова повно зв’язана структура, виходи якої замкнуті на вхід. Використовується гранична функція активації (f(s)=-1, при q<0;f(s)=1, при q>0).

Стартові ваги задаються як:

де – i-й і j-й елемент вектора k-го зразка;

m – число образів, що запам’ятовується мережею.

Рисунок 2.4 – Структура мережі Хопфілда

Мережа повинна віднести поданий на вхід сигнал до одного з векторів х_л, що зберігаються, або дати відповідь що подібних образів у мережі немає. Алгоритм зводиться до ітераційного розрахунку станів виходів нейронів:

де f – функція активації.

Цей ітераційний процес повторюється поки не перестануть змінюватися виходи нейронів. При функціонуванні мережі відбувається мінімізація «енергетичної функції»:

Cистема наблизиться до найближчого стійкого стану (аттрактору) із мінімумом потенційної енергії. З недоліків цієї моделі слід зазначити проблему ємності дотепер не вдавалося реалізувати мережу, де число збережених образів складає більш 15% від числа всіх нейронів.

Алгоритм функціонування мережі Хопфілда:

1. Формують М векторів із N компонентами .

2. На основі цих векторів формують по формулі (2.12) матрицю зв’язків мережі Хопфілда:

3. Створюють вхідний вектор, що розпізнається узявши за основу один із еталонів з масиву в М векторів (сформульованих на 1 етапі), замінюють значення b елементів на протилежні.

4. Подають на вхід мережі вектор по ітераційному алгоритмі зробивши перерахунок мережі, і після кожної ітерації фіксують вихідні вектори.

5.Визначають число ітерацій після яких сітка сходиться (розпізнає і відновлює вхідний образ(один із еталонів)).

6. Повторюють дії 3-5 для інших подібних векторів.

Якщо в мережі Хопфілда використовуються коефіцієнти зваження:

1. Виконують пункти 1-2.

2. Формують зважену матрицю β-зв’язків. Для цього необхідно подати на вхід вектор символу і порівняти його з іншими:

де П_с – кількість співпадань;

П – кількість нейронів.

3. Знаходять зважену матрицю:

4.Далі виконують пункти 4-9.

В даний час ведеться інтенсивна робота з поліпшення характеристик моделі Хопфілда, пропонуються її цікаві розширення й узагальнення. Починаються спроби створити алгоритми навчання, що дозволяють працювати з зкорельованими образами. У ряді робіт приводяться навчальні правила, що здійснюють ортогоналізацію і дозволяють запам'ятовувати в матриці зв'язків, довільний набір лінійно незалежних образів. Такі правила, однак, приводять до ускладненої нелокальної залежності матриці зв'язків від записуваних образів. Пропонуються способи відображення ієрархії зкорельованих образів, що існує в реальному світі, в ієрархічному дереві стійких станів нейроной мережі.

У деяких роботах даний аналіз появи в мережі Хопфілда помилкових образів. Вони виникають внаслідок властивого нейроній мережі властивості накопичувати в процесі навчання комбінації вхідних сигналів, що найбільше часто зустрічаються, формуючи прототипні образи. Однак ця властивість, дуже корисне для ансамблевих мереж з малим рівнем активності, для мережі Хопфілда приводить до негативного ефекту через великий рівень активності використовуваних у ній образів, а отже, значного їхнього перекриття.

Починаються пошуки способів збільшення кількості образів, яку можна запам'ятати в мережі Хопфілда. Пропонувалося ввести в модель «забування» (наприклад, обмеженням величини ваг). При цьому нові записувані в мережу образи будуть витісняти старі. У роботі вдалося домогтися збільшення числа запамятованих образів ціною введення множинних зв'язків. Однак радикального поліпшення інформаційних характеристик мережі Хопфілда, як показує аналіз, дозволяє домогтися початковий варіант хеббівського правила у мережі з низьким рівнем активності. Це підтверджується також даними дослідників, що працюють з ансамблевими мережами (див. п. 1.4.2. подп. 1).

Цікавим результатом увінчалася робота з подолання таких серйозних з біологічної точки обмежень моделі, як повнозв‘язність і симетрія. Виявилося, що сильно розріджена асиметрична версія мережі Хопфілда може бути вирішена аналітично, і її поведінка якісно схожа на поведінку повнозв‘язної мережі в області гарного відновлення.

Для мережі Хопфілда запропонований також ряд механізмів роботи з послідовностями. Основна проблема полягає в тім, щоб при запам'ятовуванні відбити в статичній структурі матриці зв'язків порядок проходження вхідних образів, а при відтворенні забезпечити їхнє відновлення в потрібному порядку. Це досягається формуванням матриці зв'язків, у якій поряд зі стаціонарними станами (симетричні зв'язки) запамятовані переходи між ними (асиметричні зв'язки від попереднього образа до наступному). Для того щоб розділити два типи динаміки — релаксацію до стійкого стану, що відповідає одному з образів послідовності, і перехід до наступного образу— було запропоновано записувати переходи між станами в окремій матриці зв'язків і ввести тимчасові затримки на сигнали, що надходять на входи нейронів через цю матрицю. Унаслідок цього мережа спочатку стабілізується в деякому стані, а вже потім починає «відчувати» вплив, що притягає, наступного стану і переходить у нього. На таких мережах була продемонстрована генерація, розпізнавання і підрахунок елементів найпростіших послідовностей, однак поки не вирішена проблема обробки більш складних послідовностей, що мають загальні частини, розгалуження і повторення.

Розвиваючи свої ідеї про «колективні обчислення» у нейроних мережах, Хопфілд запропонував використовувати властивість мережі мінімізувати енергетичну функцію для рішення оптимізаційних задач. З цією метою спочатку вибирається «нейроне» представлення для конкретної задачі, тобто виходячи з її умов стану нейронів присвоюється смисл. Потім з урахуванням обмежень, що накладаються на задачу, конструюється енергетична функція таким чином, щоб у станах, що представляють можливі рішення, вона була пропорційна вартісної функції задачі. Після цього з енергетичної функції витягаються зв'язки w_ij і пороги θ_i і конструюється відповідна мережа. Тому що в процесі функціонування мережа мінімізує свою енергію, динаміка в просторі станів спрямована на мінімізацію відповідної вартісної функції. Пошук мінімуму енергії займає усього декілька постійних часу нейронів, тому мережа швидко досягає стабільного стану, з якого декодується рішення задачі. Тому що тут на відміну від задачі асоціативної пам'яті потрібно знаходження не локального, а глобального енергетичного мінімуму, сутьєвою виявляється сигмоїдність характеристик нейронів (бінарні нейрони тут не підходять) і аналоговий характер їхньої взаємодії. Рішення, що знаходяться такою аналоговою мережею, не найкращі, але досить близькі до них.

Незважаючи на недоліки мережі Хопфілда, починаються спроби використовувати її апаратні реалізації, для рішення задач, що вимагають швидкого розпізнавання невеликої кількості простих образів.