6. Понятие об инкрементных алгоритмах растеризации. Построение окружности методом средней точки. Вывод и реализация алгоритма

Брезенхэм предложил подход, позволяющий разрабатывать так назы­ваемые инкрементные алгоритмы растеризации. Основной целью для разра­ботки таких алгоритмов было построение циклов вычисления координат на основе только целочисленных операций сложения/вычитания без использо­вания умножения и деления. Инкрементные алгоритмы выполняются как последовательное вычисление координат соседних пикселов путем добавления приращений координат.

Разработаны инкрементные алгоритмы для вывода отрезка, окружности, эллипса.

Алгоритм построения окружности методом средней точки

Рассмотрим уравнение окружности радиуса 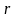с центром в начале координат

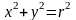(1)

Введем в рассмотрение функцию окружности (2)

Любая точка 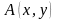, которая лежит на окружности удовлетворяет урав­нению

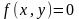
Если точка находится внутри круга, то функция окружности будет иметь отрицательное значение. Если точка лежит за пределами круга, значение функции окружности будет положительным. Подытоживая, можно сказать, что от­носительное положение любой точки с координатами определяется проверкой знака функции окружности:

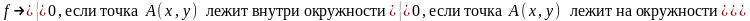(3)

Проверка выполняется на каждом этапе выборки для средних положений между пикселями вблизи заданной окружности. Таким образом, функция окружности – это параметр принятия решения в алгоритме средней точки, и для этой функции можно установить операции приращения, как это было сделано для алгоритма построения прямой линии.

На рис. показана средняя точка между двумя возможными пикселями в точке выборки. Предположим, что мы только что поставили точку в пикселе с коорди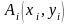натами Теперь нужно определить, какой из двух пикселей ближе к заданной окружности – пиксель с координатами 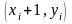или пиксель с координатами 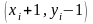Параметром принятия решения будет функция окружности (3), которая рассчитывается для средней точки между этими двумя пикселями:

В случае, когда 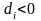, полагаем . Тогда

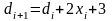
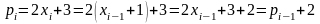
При этом

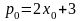
Тогда

,

,

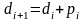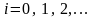
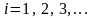
В случае, когда 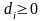, делаем шаг вниз, полагая 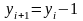. Тогда

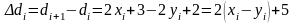
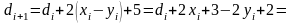
Где

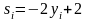
Для рассматриваемого случая, когда ,

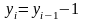
При этом

Тогда

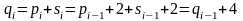
Таким образом

,

,

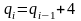Для случая, когда ,

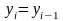
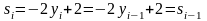
И выражение для 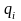принимает вид

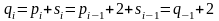
При этом

,

,

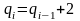Таким образом,

если

,

,

,

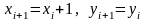
если

,

,

,

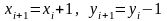
Для удобства заменим в выражениях для 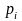и на , тогда

если

,

,

,

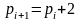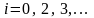
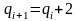если

,

,

,

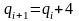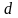
Начальные значения параметров 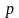и определим из условия 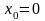и

Тогда

Поскольку радиус и приращение, 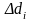целые числа, то значение можно округлить и принять

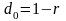
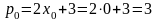
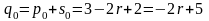
Алгоритм поэтапно:

• Установить начальные значение для

• Поставить начальные точки

• Выполнять в цикле пока

• если

,

,

,

• если

,

,

,

• Поставить точки, соответствующие текущему шагу

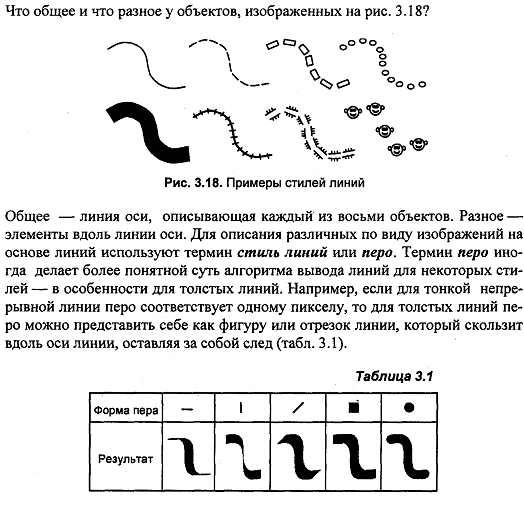
7. Стиль линии (перо). Алгоритм вывода линии

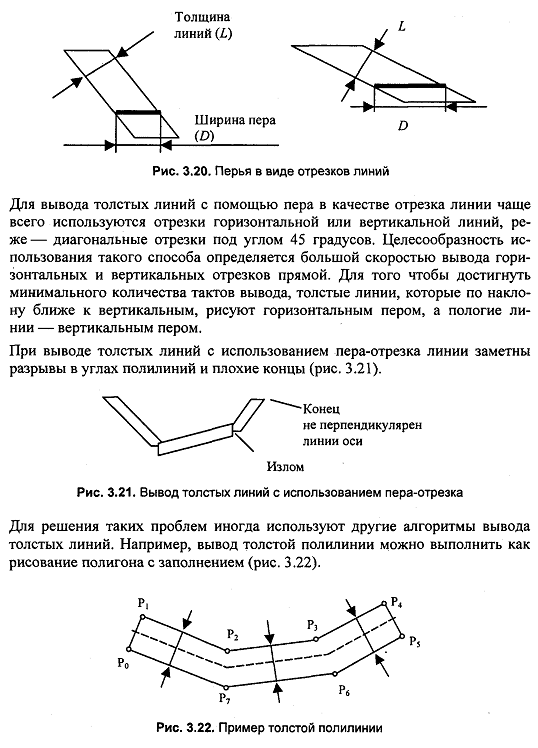
8. Стиль заполнения, кисть, текстура

Для обозначения стилей заполнения, отличных от сплошного стиля, используют такие понятия, как кисть и текстура. Текстура – это стиль заполнения, закрашивание, которое имитирует сложную рельефную объемную поверхность, выполненную из какого-то материала.

Для описания алгоритмов заполнения фигур с определенным стилем исполь­зуем следующий алгоритм рисования линий:

• вывод пиксела заполнения цвета C с координатами (х, у)

Например, в алгоритме вывода полигонов пикселы заполнения рисуются в теле цикла горизонталей, а все другие операции предназначены для подсчета координат (х, у) этих пикселов. Сплошное заполнение означает, что цвет (С) всех пикселов одинаков, то есть C = const. Преобразуем ал­горитм заполнения следующим образом:

• С = f (х, у)

• вывод пиксела заполнения (х, у) цветом C.

Функция f(x, y) будет определять стиль заполнения. Аргументами функции цвета являются координаты текущего пиксела заполнения. Однако в отдельных случаях эти аргументы не нужны. Например, если цвет C вычисляется как случайное значение в определённых границах: С = random(), то можно создать иллюзию шершавой матовой поверхности (рис. 3.23).

Другой стиль заполнения – штриховой. Для него функцию цвета также можно записать в аналитической форме:

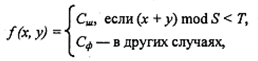
где S – период, а T – толщина штрихов, C_ш – цвет штрихов, Cф – цвет фона.

Зачастую при использовании кистей и текстур используется копирование не­больших растровых изображений. Такой алгоритм заполнения можно опи­сать вышеупомянутой общей схемой, если строку С = f (х, у) заменить двумя другими строками:

• координаты пиксела заполнения (х, у) преобразуем в растровые координаты образца кисти (х_т / y_т)

• по координатам (х_т / y_т) определяем цвет (С) пиксела в образце кисти

• вывод пиксела заполнения цвета С c координатами (х, у)

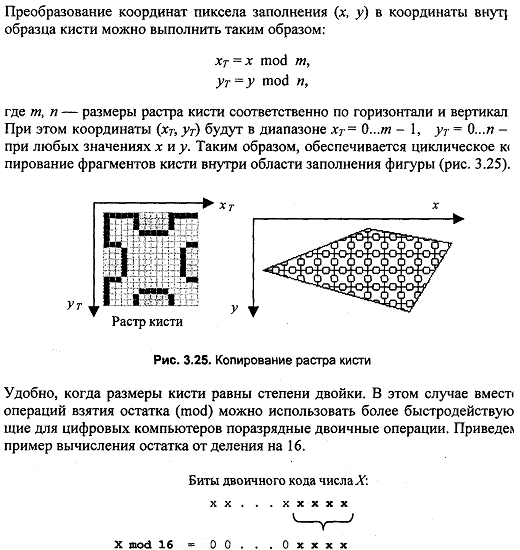
Преобразование координат пиксела заполнения (х, у) в координаты внутри образца кисти можно выполнить таким образом:

х_т = х mod m,

y_т = y mod n,

где m, n – размеры растра кисти соответственно по горизонтали и вертикали. При этом координаты (х_т, y_т) будут в диапазоне х_т = 0...m - 1, y_т = 0...n – при любых значениях х и у. Таким образом, обеспечивается циклическое копирование фрагментов кисти внутри области заполнения фигуры.

Проективные текстуры

Поскольку объекты часто показываются с разных ракурсов – повороты, изменения размеров и т. п., то необходимо трансформировать соответственно и каждую грань с текстурой. Для этого используются проективные текстуры.