Линейная регрессия
Линейная регрессия, или линейная форма связи между случайными переменными занимает особое место в теории корреляции. При такой форме связи У есть линейная функция от Х, т. е.
У = а + bХ ,
где а и b – коэффициенты регрессии, Х – независимая случайная переменная. Линейная регрессия обусловливается двумерным нормальным законом распределения пары случайных величин (Х, У).
Параметры в уравнении регрессии, т. е. коэффициенты регрессии, определяются по способу наименьших квадратов. Суть его заключается в том, чтобы сумма квадратов отклонений измеренных величин от истинного значения была бы минимальной.
В случае линейной регрессии за теоретическое значение принимается значение У, получаемое по известной формуле, т. е. ищется такая прямая линия, сумма квадратов отклонений измеренных Уi от которой была бы минимальной.
Значения коэффициентов регрессии определяются решением системы нормальных уравнений.
Расчёт коэффициентов уравнений линейной регрессии
Как уже было сказано выше, в случае линейной зависимости уравнение регрессии является уравнением прямой линии.
Различают
У = ау/х +bу/хХ - прямое уравнение регрессии;
Х = ах/у+bх/у Y - обратное уравнение регрессии.
Здесь а и b – коэффициенты, или параметры, которые определяются по формулам. Значение коэффициента b вычисляется
Из формул видно, что коэффициенты регрессии bу/х и bх/у имеют тот же знак, что и коэффициент корреляции, размерность, равную отношению размерностей изучаемых показателей Х и У, и связаны соотношением:
Для вычисления коэффициента а достаточно подставить в уравнения регрессии средние значения коррелируемых переменных
График теоретических линий регрессии (рис. 17) имеет вид:
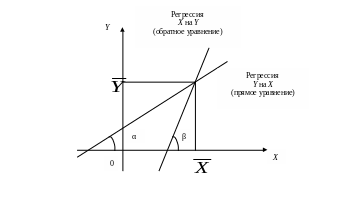
Рис 17. Теоретические линии регрессии
Из приведённых выше формул легко доказать, что угловые коэффициенты прямых регрессии равны соответственно
Так
как
,
то
.
Это означает, что прямая регрессии Y
на Х
имеет меньший наклон к оси абсцисс, чем
прямая регрессии Х
на Y.
Чем
ближе
к единице, тем меньше угол между прямыми
регрессии. Эти прямые сливаются только
тогда, когда
.
При
прямые регрессии описываются уравнениями
,
.
Таким образом, уравнения регрессии позволяют:
определить, насколько изменяется одна величина относительно другой;
прогнозировать результаты.
2. Методика выполнения расчётно-графической работы №2
Расчётно-графическая работа содержит 4 раздела.
В первом разделе:
Формулируется тема;
Формулируется цель работы.
Во втором разделе:
Формулируется условие задачи;
Заполняется таблица исходных данных выборки.
В третьем разделе:
Результаты измерений представляются в виде вариационного ряда;
Даётся графическое представление вариационного ряда.
Формулируется вывод.
В четвёртом разделе:
Рассчитываются основные статистические характеристики ряда измерений;
По итогам расчётов формулируется вывод.
Оформление работы:
Работа выполняется в отдельной тетради или на форматных листах.
Титульный лист заполняется по образцу.
Российский Государственный Университет
физической культуры, спорта, молодёжи и туризма
Кафедра естественнонаучных дисциплин
Корреляционный и регрессионный анализы
Расчётно-графическая работа №2
по курсу математики
Выполнил: студент 1 к. 1 пот. 1гр.
Иванов С.М.
Преподаватель :
доц. кафедры ЕНД и ИТ
(Ф.И.О.)