2.5.4. Дискретный аналог критерия устойчивости Найквиста

Устойчивость замкнутой дискретной САУ с единичной обратной связью можно определить по ЗФП разомкнутой САУ с использованием дискретного аналога частотного критерия устойчивости Найквиста, дополненного Михайловым для астатических САУ, либо с использованием логарифмических псевдочастотных характеристик. В обоих случаях для устойчивости замкнутой САУ её амплитудно-фазовая характеристика (АФХ) в разомкнутом состоянии САУ не должна охватывать точку (–1, j0) на комплексной плоскости, а запаздывание выходного сигнала по фазе по псевдочастотным логарифмическим характеристикам не должно достигать –180⁰ при единичном модуле коэффициента передачи [1].

При вычислении АФХ по ЗФП W(z) разомкнутой САУ математическое описание АФХ представляется трансцендентной периодической функцией с периодом 2π/T, неудобной для расчетов. Например, если разомкнутая САУ состоит из импульсного элемента, экстраполятора нулевого порядка и интегрирующего ОУ, то её ЗФП будет иметь вид:

(2.5.16)

а АФХ, после подстановки в (2.5.16), опишется уравнением:

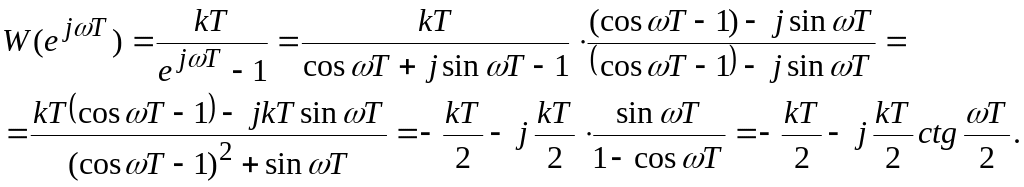(2.5.17)

Полученное трансцендентное выражение АФХ очень неудобно для расчетов дискретных САУ. Поэтому было введено понятие псевдочастотных характеристик, которые получаются из ЗФП W(z) при введении билинейного преобразования Мебиуса w=(z-1)/(z+1), из которого z=(1+w)/(1-w). При введении этого преобразования в характеристическое уравнение M(z)=0, граница устойчивости дискретной САУ на плоскости корней z_i в виде единичной окружности преобразуется в мнимую ось на комплексной плоскости корней w_i, где вся левая полуплоскость будет областью устойчивости, как в непрерывных САУ. Это позволяет исследовать устойчивость дискретных САУ с характеристическим полиномом M(w)=0 по критериям устойчивости линейных непрерывных САУ. При преобразовании границы устойчивости дискретной САУ на комплексной плоскости z_i-корней, где она описывается уравнением единичной окружности z=1∙e^jωT, в границу устойчивости в виде мнимой оси на комплексной плоскости w_i-корней, описание границы устойчивости получается в виде:

(2.5.18)

где – относительная безразмерная псевдочастота, изменяющаяся от 0 до ∞; – абсолютная псевдочастота, 1/cек.

Для разомкнутой САУ с ЗФП (2.5.16) введение w-преобразования приводит к получению передаточной функции в виде:

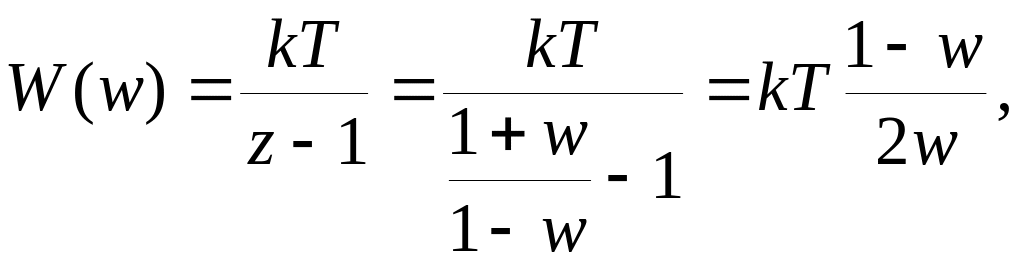(2.5.19)

из которой, после подстановки значения из (2.5.18) и избавления от мнимости в знаменателе, получим выражение амплитудно-фазовой псевдочастотной характеристики (АФПЧХ) разомкнутой САУ в виде:

(2.5.20)

где – абсолютная псевдочастота, 1/c.

Амплитудная псевдочастотная характеристика (АПЧХ):

(2.5.21)

Фазовая псевдочастотная характеристика (ФПЧХ) будет:

(2.5.22)

Логарифмическая амплитудная псевдочастотная характеристика (ЛАПЧХ) САУ запишется в виде:

(2.5.23)

ЛАПЧХ по (2.5.23) состоит из двух асимптот, которые сопрягаются при псевдочастоте λ _С =2/T:

1) при λ _C ≤ 2/T – асимптота с наклоном –20 дб/дек;

2) при λ _C ≥ 2/T – горизонтальня асимптота.

Частота среза ЛАПЧХ определяется из равенства нулю ЛАПЧХ по (2.5.23) или из равенства единице АПЧХ по (2.5.21):

(2.5.24)

Устойчивость и запасы устойчивости дискретных САУ определяются по псевдочастотным характеристикам так же, как по частотным характеристикам в непрерывных САУ. Следует отметить сильное влияние на устойчивость и другие свойства дискретных САУ величины периода квантования Т.

Пример 2.5.4. Исследуем устойчивость замкнутой дискретной САУ с единичной обратной связью, если её ЗФП в разомкнутом состоянии имеет вид [1]:

(2.5.25)

Для перехода к w-преобразованию вводим в (2.5.25) первую подстановку z=(1+w)/(1–w) и получаем передаточную функцию в виде:

(2.5.26)

Для получения псевдочастотной передаточной функции (АФПЧХ) разомкнутой дискретной САУ вводим в (2.5.26) вторую подстановку w=jTλ/2 [1]:

(2.5.27)

Модуль коэффициента передачи из (2.5.27) или амплитудная псевдочастотная характеристика A*(λ) разомкнутой САУ представляется выражением:

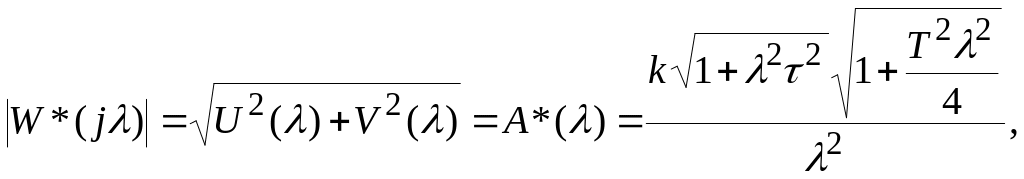(2.5.28)

а фазовая псевдочастотная характеристика определяется из (2.5.27) последовательно соединенными интегрирующим звеном второго порядка с W(jλ)=k/(jλ)², форсирующим (ускоряющим) звеном с W(jλ)=(1+jτλ) и инерционным (замедляющим) звеном с W(jλ)=(1–jTλ/2) (рис. 2.5.2):

(2.5.29)

Асимптотическая ЛАПЧХ разомкнутой САУ, построенная по (2.5.28), состоит из трех слагаемых, образующих три асимптоты (рис. 2.5.2)

(2.5.30)

Рис. 2.5.2. ЛАПЧХ и ЛФПЧХ разомкнутой САУ.

Рис. 2.5.2. ЛАПЧХ и ЛФПЧХ разомкнутой дискретной САУ

Замкнутая САУ будет устойчива, если АФПЧХ W*(λ) разомкнутой САУ (2.5.27) при изменении частоты λ от 0 до ∞ не охватывает на комплексной плоскости точку (–1; j0) или если при частоте среза λ_С запаздывание выходного сигнала по фазе по ЛФПЧХ φ*(λ_С) не достигает –180⁰. Частота среза λ_C определяется из равенства единице выражения в круглых скобках в (2.5.30).

Запас устойчивости по фазе Δφ_ЗАП(λ_С)=–180⁰+|φ*(λ_С)| определяется по ЛФПЧХ φ*(λ) при λ = λ_С, запас устойчивости по амплитуде ΔL_ЗАП определяется по ЛАПЧХ L*(λ₁₈₀) при достижении по ЛФПЧХ φ*(λ₁₈₀)=–180⁰ (рис. 2.5.2).