
- •2. Расчет линейных дискретных систем управления
- •2.1. Описание дискретных сау дискретно-разностными уравнениями
- •2.2. Вычисление z–преобразований от заданных функций
- •2.3. Расчет передаточных функций импульсных систем
- •2.3.1. Математическая модель импульсного элемента
- •2.3.2. Передаточные функции разомкнутых систем
- •2.3.3. Передаточные функции замкнутых систем
- •2.4. Расчет передаточных функций цифро-аналоговых сау
- •2.4.1.Передаточные функции разомкнутых цас
- •2.4.2.Передаточные функции замкнутых цас
- •2.5. Расчет устойчивости дискретных сау
- •2.5.2. Дискретный аналог критерия устойчивости Гурвица
- •То из (2.5.5) характеристическое уравнение замкнутой сау будет равно:
- •Определитель Гурвица для уравнения третьего порядка запишется:
- •2.5.3. Дискретный аналог критерия устойчивости Михайлова
- •2.5.4. Дискретный аналог критерия устойчивости Найквиста
- •2.6. Расчет качества дискретных сау
- •2.6.1.Расчет точности в установившихся режимах
- •2.6.2. Расчет качества переходных процессов
- •Список литературы
- •Содержание
- •2. Расчет линейных дискретных систем управления. . . . . . . . . . . . . . 14
2.2. Вычисление z–преобразований от заданных функций
Вычисление Z–преобразований от типовых функций времени, имеющих табличные Z–изображения, выполняются непосредственно по их табличным Z–изображениям. Если заданная функция времени представлена суммой табличных типовых функций:
![]() (2.2.1)
(2.2.1)
то Z-изображение суммы табличных функций времени представляется простой суммой Z-изображений каждой из функций в виде:
 (2.2.2)
(2.2.2)
где Т – период дискретизации (период квантования) сигнала.
Вычисление Z–преобразования от дробной функции F(p) или W(p) с разложением её методом неопределенных коэффициентов на простые дроби, имеющие табличные Z–изображения:
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2.2.3)
(2.2.3)
2.3. Расчет передаточных функций импульсных систем
2.3.1. Математическая модель импульсного элемента
Основным звеном
типовой импульсной САУ (рис. 2.1.1,а)
является импульсный
элемент
(ИЭ), который
преобразует непрерывный сигнал ошибки
x(t)
в решетчатую
функцию
– последовательность
мгновенных импульсов x[nТ]
с периодом
квантования T=const
и величиной дискрет x[n]=x(t)t=nT.
При этом полагают, что идеальный
ИЭ формирует
импульсы в виде дельта-функций
Дирака
![]() из которых
формирователь
импульсов (экстраполятор)
WЭ(р)
формирует
решетчатую функцию из реальных импульсов
напряжения прямоугольной, треугольной
или иной формы. Для этого экстраполятор
должен иметь импульсную переходную
характеристику, совпадающую с требуемой
формой выходных импульсов реального
ИЭ [1]. Для формирования прямоугольных
импульсов в реальной САУ с
амплитудно-импульсной модуляцией на
выходе ИЭ должен использоваться
экстраполятор с импульсной переходной
характеристикой, образованной двумя
ступенчатыми функциями времени
КЭ(t)=1[t]–1[t–τИ],
где τИ
<
Т (Т
- период
квантования импульсов).
В этом случае,
с использованием обыкновенного
преобразования Лапласа и теоремы о
смещении функции во времени, ОФП
формирователя прямоугольных импульсов
(рис. 2.1.1) представляется в виде [1]:
из которых
формирователь
импульсов (экстраполятор)
WЭ(р)
формирует
решетчатую функцию из реальных импульсов
напряжения прямоугольной, треугольной
или иной формы. Для этого экстраполятор
должен иметь импульсную переходную
характеристику, совпадающую с требуемой
формой выходных импульсов реального
ИЭ [1]. Для формирования прямоугольных
импульсов в реальной САУ с
амплитудно-импульсной модуляцией на
выходе ИЭ должен использоваться
экстраполятор с импульсной переходной
характеристикой, образованной двумя
ступенчатыми функциями времени
КЭ(t)=1[t]–1[t–τИ],
где τИ
<
Т (Т
- период
квантования импульсов).
В этом случае,
с использованием обыкновенного
преобразования Лапласа и теоремы о
смещении функции во времени, ОФП
формирователя прямоугольных импульсов
(рис. 2.1.1) представляется в виде [1]:
![]() (2.3.1)
(2.3.1)
2.3.2. Передаточные функции разомкнутых систем
Разомкнутая
импульсная система с амплитудно-импульсной
модуляцией (АИМ) при длительности
импульсов τИ
<
Т
состоит из
ИЭ, формирователя прямоугольных импульсов
(экстраполятора нулевого порядка) WЭ(р)
и непрерывной части WН(р),
включающей датчик обратной связи (рис.
2.1.1, а). ИЭ формирует из непрерывного
сигнала ошибки его решетчатую функцию
в форме дельта-функций,
а эктраполятор и непрерывная часть
импульсной системы образуют импульсный
фильтр
![]() ,
не пропускающий пульсации импульсного
сигнала на выход y(t).
ОФП импульсного фильтра и всей разомкнутой
системы с АИМ и экстраполятором нулевого
порядка описывается выражением [1]:
,
не пропускающий пульсации импульсного
сигнала на выход y(t).
ОФП импульсного фильтра и всей разомкнутой
системы с АИМ и экстраполятором нулевого
порядка описывается выражением [1]:
![]() (2.3.2)
(2.3.2)
При этом зет-функция передачи (ЗФП) импульсного фильтра и всей разомкнутой САУ определяется выражением [1]:
![]() (2.3.3)
(2.3.3)
В САУ с АИМ, где ИЭ формирует прямоугольные импульсы с τИ = γТ при γ < 1, способные непосредственно воздействовать на непрерывную часть WH(p), экстраполятор не нужен. При этом изображение единичных импульсов по Лапласу представляется выражением:
![]() (2.3.4)
(2.3.4)
а зет-функция передачи разомкнутой САУ (рис. 2.1.1, а) будет [1, 2]:
![]() (2.3.5)
(2.3.5)
где Zε – Z-изображение смещенной функции, ε=1–γ – смещение.
Пример 2.3.1. Определить ЗФП W(z) разомкнутой импульсной САУ, имеющей ИЭ с периодом квантования Т=0,1 с, экстраполятор нулевого порядка (с фиксацией на период квантования Т) и непрерывную часть с ОФП WH(p)=K/p(1+pTH) при K=100 c–1 и TH=0,5c.
По (2.3.3) W(z)=(1–z–1)Z{WH(p)/p}=(1–z–1)Z{K/p2(1+pTH)}.
Для определения Z-изображения дроби в фигурных скобках, разложим эту дробь методом неопределенных коэффициентов на сумму простых дробей, имеющих табличные Z-изображения [1]:

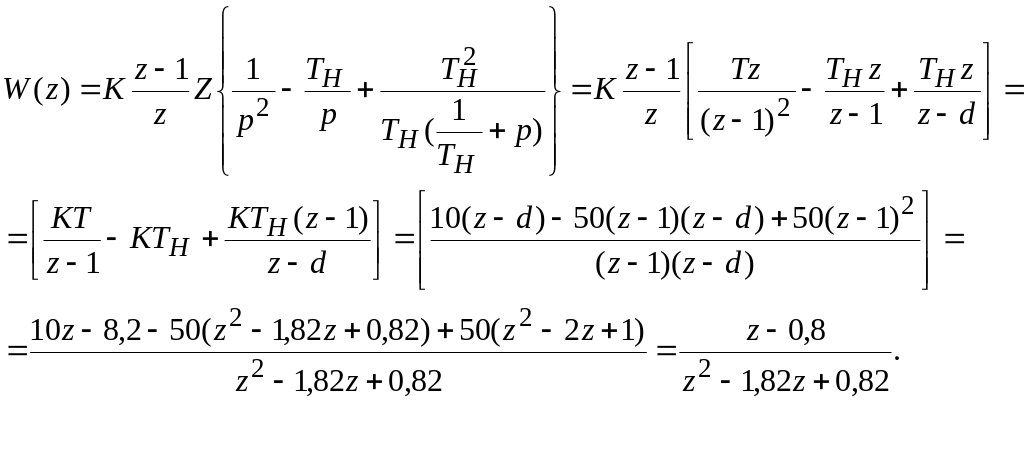 (2.3.6)
(2.3.6)
где α= 1/TH = 1/0,5=2 c–1, d=e–αT=1/eαT = 1/e2·0,1=1/1,22=0,82.
