9.6 Системи передачі із шумоподібними сигналами

Розглянуті вище системи багатоканальної передачі з ортогональними та лінійно незалежними сигналами вимагають для нормальної роботи системи синхронізації; котра необхідна для: точного збігу спектра сигналу зі смугою пропускання при ЧРК; точного збігу часових інтервалів передачі сигналів окремих каналів при РКЧ; точного визначення моментів початку й кінця тактового інтервалу в системах з розподілом активними фільтрами сигналів за формою; точної установки моменту відліку в системі з узгодженими фільтрами.

У ряді випадків здійснити точну синхронізацію важко. З подібними ситуаціями доводиться зустрічатися, наприклад, при організації оперативного зв'язку між рухомими об'єктами (автомобілями, поїздами, літаками та ін.). Таке завдання виникає також при організації оперативного зв'язку коли штучні супутники Землі використовуються як ретранслятори. У всіх цих випадках можуть бути використані системи асинхронного багатоканального зв'язку, коли сигнали всіх абонентів передаються в спільній смузі частот, а канали не синхронізовані між собою в часі.

Оскільки в таких системах за каналами не закріплені ні частотні смуги, ні часові інтервали й час роботи кожного каналу довільний, то такі системи називають системами з вільним доступом до лінії зв'язку або системами з незакріпленими каналами. У системах з вільним доступом кожному каналу (абонентові) присвоюється певна форма сигналу, яка і є відмітною ознакою, «адресою» даного абонента. На відміну від звичайного розподілу за формою, де умова ортогональності сигналів виконуються лише тоді, коли тактові інтервали всіх каналів жорстко синхронізовані, щоб мати змогу повного лінійного розподілу сигналів у системах з вільним доступом ортогональність або лінійна незалежність повинні зберігатися при будь-яких часових зсувах сигналів. Це значить, що для будь-якої пари сигналів і повинна виконуватися умова

^(9.24)

при , де – тривалість елементарного сигналу, а інтегрування відбувається на будь-якому інтервалі від до .

Строго кажучи, умова (9.24) виконується тільки у випадку, коли сигнали являють собою білий шум, тобто мають необмежену ширину спектра й нескінченну дисперсію; для реальних сигналів вона нездійсненна. Разом з тим можна сформувати такі сигнали, для яких (9.24) виконується приблизно в тому розумінні, що

при , ^(9.24а)

тобто скалярні добутки сигналів при будь-якому зсуві за часом набагато менші енергії елементарного сигналу. Такі сигнали можна назвати майже ортогональними. За своїми властивостями майже ортогональні сигнали наближаються до білого шуму, тому їх часто називають широкосмуговими шумоподібними (ШШС). Їхні кореляційні функції й спектри щільності потужності близькі до аналогічних характеристик квазібілого шуму. Шумоподібні сигнали належать до класу складних сигналів, база яких , і є подальшим розвитком сигналів, що розрізняються за формою.

Теорії шумоподібних сигналів і питанням їхнього використання в різних системах зв'язку присвячені роботи Л.Е. Варакіна [11].

Найпоширенішим прикладом технічної реалізації майже ортогональних шумоподібних сигналів можуть бути певним чином сформовані псевдовипадкові послідовності дискретних, зокрема, двійкових радіоімпульсів. База сигналів при цьому визначається кількістю імпульсів у послідовності. Кожному каналу присвоюється одна з множин майже ортогональних двійкових послідовностей, яка і є «адресою» каналу. Це приводить до назви «асинхронні адресні системи зв'язку» (ААСЗ).

Важливою перевагою ААСЗ є те, що немає потреби мати центральну комутаційну станцію; у всіх абонентів є прямий доступ один до одного без частотної перебудови прийомних і передавальних пристроїв (рис. 9.9). Тут досить набрати «адресу» абонента, що викликається, тобто змінити «форму» імпульсної адресної послідовності.

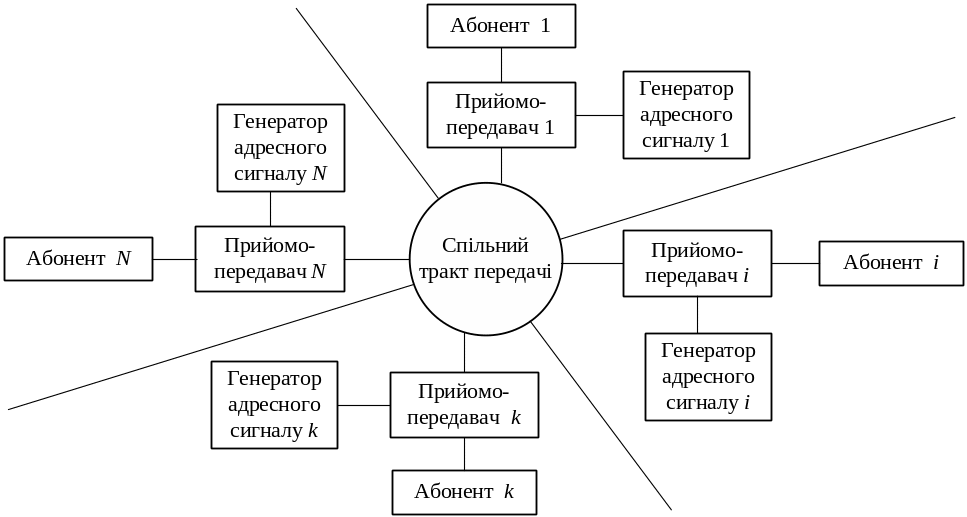
Рисунок 9.9 – Структурна схема багатоканальної асинхронно-адресної системи зв'язку

У системах із закріпленими каналами з ЧРК і РКЧ додавання хоча б одного нового абонента виявляється можливим лише при виключенні одного з тих, що є в системі. Значно простіше це завдання вирішується в системах ААСЗ. Тут внаслідок вільного доступу до лінії зв'язку можуть вести передачу будь-які активних абонентів із загального числа абонентів системи зв'язку.

При визначенні числа потрібно враховувати, що внаслідок неповної ортогональності каналів в ААСЗ неминучі перехідні завади («шуми неортогональності»), рівень яких зростає в із збільшенням . Тому кількість одночасно працюючих абонентів повинна бути обмежена. Припустиме значення зростає в міру збільшення бази сигналу, тому що чим більша база, тим точніше виконується умова (9.24, а).

Залежно від часу активності абонентів (тобто від частки часу, яку займає -й канал для передачі повідомлень) можна організувати, наприклад, 1000-канальну систему зв'язку, у якій одночасно проводиться передача будь-яких 50 абонентів з тисячі. У таких системах легко реалізуються резерви пропускної здатності, які виникають за рахунок малоактивних абонентів. Вивчивши статистику повідомлень, переданих по кожному каналу, можна встановити припустиме число каналів у системі , при якому забезпечується нормальна робота активних каналів.

Приклади шумоподібних сигналів. В теперішній час посилено розробляються методи синтезу сигналів із заданими автокореляційними (АКФ) та взаємно кореляційними функціями (ВКФ). Якщо розглядати послідовності з імпульсів прямокутної форми, які можуть приймати значення ±1, то простим перебором можна знайти такі послідовності, для яких , , , – енергія всього сигналу, – енергія одного елемента. Серед них назвемо насамперед послідовності коду Баркера (табл. 9.1) [19].

Послідовності Баркера мають близьку до ідеальної форми автокореляційну функцію: абсолютне значення бічних пелюстків не перевищує загального. На рис. 9.10,а наведена послідовність (яка називається також кодом) Баркера для і її автокореляційна функція (рис. 9.10,б).

Таблиця 9.1 – Структури послідовностей коду Беркера

Кіль­кість імпульсів	Номер імпульсу в послідовності																Максимум; нормованого модуля АКФ
	1	2	3	4		5	6	7	8	9	10	11		12		13	основний	побічні
2	+1	-1															1	1/2
3	+1	+1	-1														1	1/З
4	+1	+1	-1		+1												1	1/4
5	+1	+1	+1		-1	+1											1	1/5
7	+1	+1	+1		-1	-1	+1	-1									1	1/7
11	+1	+1	+1		-1	-1	-1	+1	-1	-1	+1		-1				1	1/11
13	+1	+1	+1		+1	+1	-1	-1	+1	+1	-1		+1		-1	+1	1	1/13

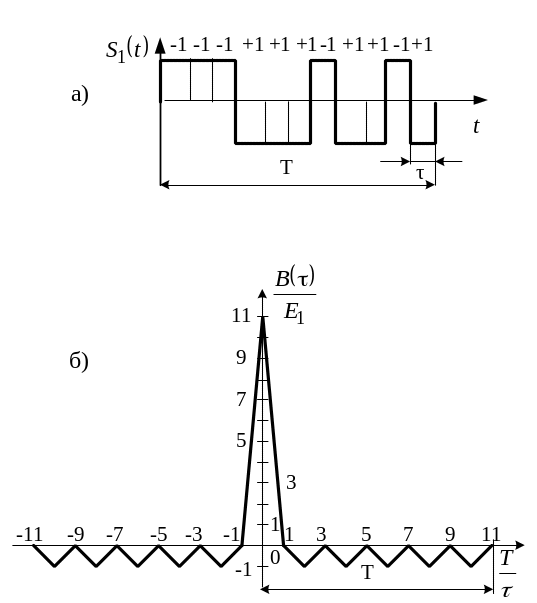
Рисунок 9.10 - Реалізація послідовності Баркера (а) і її автокореляційна функція (б)

Прийом послідовності («адреса» 1 каналу) рис. 9.10,а виконується узгодженим трансверсальним фільтром рис. 9.11. Імпульси послідовності Баркера з кількістю знаків надходять спочатку на фільтр УФ_ПІ, узгоджений з одиничним прямокутним імпульсом, а потім у лінію затримки (ЛЗ), яка має відводи через проміжки , далі на фазоінверсні (–) і фазозберігаючі (+) каскади з однаковими коефіцієнтами передачі, складаючий й вирішуючий пристрій (ВП).

Фазоінверсні та фазозберігаючі каскади ввімкнені в порядку, що відповідає зворотному порядку чергування біполярних імпульсів -послідовності (рис. 9.10,а): кількість цих каскадів дорівнює кількості елементів послідовності. Перший каскад ввімкнений перед лінією затримки, останній – на її кінці.

При прийомі -послідовність проходить по ЛЗ, і в момент, коли всі імпульси послідовності співпадуть за знаком з вагами, ввімкненими між відводами ЛЗ і складаючим пристроєм, всі імпульси складуться синфазно, на виході ВП з'явиться найбільший імпульс – узгоджений фільтр зафіксує адресу 1-го каналу.

При всіх інших зсувах підсумовування відбувається не у фазі (з різними знаками), і на виході ВП з'являються рівні, що не перевищують по модулю від максимального значення. Оскільки функції взаємної кореляції між послідовностями також мають найбільші значення, що не перевищують , то послідовність адреси чужого каналу не може викликати помилкового спрацьовування вирішуючого пристрою 1-го каналу.

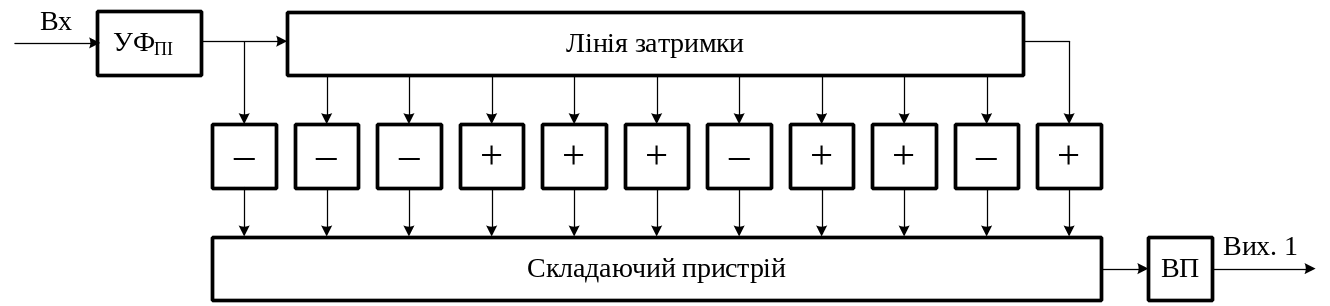
Рисунок 9.11 - Узгоджений фільтр для послідовності Баркера

Дослідження показують, що послідовностей Баркера із «залишками» величини для не існує. Тому для більших доводиться задовольнятися послідовностями, які мають «залишки» більші, ніж .

Трохи гірші автокореляційні функції порівняно з послідовностями Баркера, але все ж таки досить придатні для використання в якості адресних сигналів мають лінійні рекурентні  - послідовності (ЛРП) або, як їх ще називають, лінійні послідовності зсувного регістра формуючого послідовність максимальної довжини. Для ЛРП відношення головного максимуму до максимального бічного пелюстка автокореляційної функції зростає приблизно як , де – кількість імпульсів у послідовності.

Лінійним рекурентним послідовностям притаманна властивість хаотичності, що полягає в наступному. Якщо з періоду ЛРП, що містить членів, вибрати можливі відрізки членів у кожному, то, по-перше, серед цих відрізків не буде тих, що співпадають і, по-друге, серед них знайдуться будь-які комбінації з +1 та –1, що складаються з членів (окрім забороненої комбінації, яка складається тільки з +1). Ці властивості подібні до властивостей випадкових біполярних послідовностей; тому ЛРП часто називають псевдовипадковими або шумоподібними послідовностями.

До того ж автокореляційна функція ЛРП має форму, подібну до автокореляційної функції квазібілого шуму з обмеженим спектром. ЛРП формуються генераторами двійкових імпульсів з використанням зсувного регістра. Прийом ЛРП може здійснюватися як узгодженими фільтрами, так і кореляторами. При передачі псевдовипадкових послідовностей по високочастотному каналу зазвичай застосовується фазова або відносна фазова модуляція.

З інших способів формування ШШС для асинхронно-адресних систем зв'язку згадаємо про спосіб формування сигналів за допомогою частотно-часової матриці (ЧЧМ). Уже відзначалося, що в системах з ортогональними сигналами енергія кожного сигналу повністю відокремлюється від енергії інших сигналів. Це положення стає найбільш виразним, якщо звернутися до частотно-часових діаграм системи зв'язку при частотному розподілі (рис. 9.12,а) і при часовому розподілі сигналів (рис. 9.12,б). Тут кожному каналу відводиться певна область частотно-часового простору; положення площадки можна розглядати як «адресу» абонента.

Рисунок 9.12 – Принцип частотного (а) і часового (б) розподілу каналів

`

Однак, частотно-часову область і можна розділити на площадки іншим способом: адресу кожного каналу можна сформувати з набору «елементарних площадок» частотно-часової площини (рис. 9.13). Кожен двійковий інформаційний символ (рис. 9.13,а) передається за час і відображається певною послідовністю імпульсів, які мають різні частоти (рис. 9.13,б) у спільній смузі . Двійкову інформацію в послідовність можна закласти, міняючи один з параметрів елементарного радіоімпульсу. Ці адресні набори імпульсів складаються на основі їхнього подання у вигляді ЧЧМ (рис. 9.13,в); до них висуваються звичайні вимоги автокореляційних функцій (з малими бічними пелюстками) і малих значень взаємної кореляції.

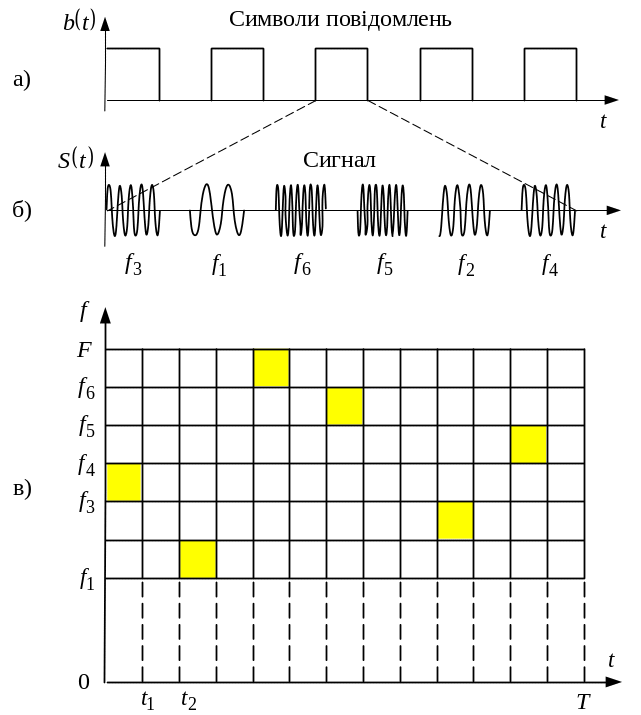
а – послідовність двійкових інформаційних сигналів;

б – подання одного двійкового імпульсу за допомогою послідовного набору радіоімпульсів різних частот;

в - подання сигналу у вигляді ЧЧМ.

Рисунок 9.13 – Приклад утворення багатоканального широкосмугового сигналу за допомогою частотно-часової матриці

Зміна часового положення імпульсів і розходження в їх частотах дозволяють порівняно простими технічними засобами одержати кілька тисяч частотно-часових коливань (адрес). Не всі комбінації ЧЧМ використовують як адресні сигнали; серед них зустрічаються й такі, які не мають необхідних кореляційних властивостей. Максимальна кількість адрес, для яких рівень бічних пелюстків кореляційних функцій не перевищує , наближається до Сигнали ЧЧМ також є різновидом сигналів, що різняться за формою. Їх також можна розподілити як узгодженими фільтрами, так і кореляторами.

В технічній літературі є опис великої кількості різних систем зв'язку з вільним доступом. Найхарактернішими з них є системи на 1000...1500 каналів з 50...100 активними абонентами.