9.4.3 Розподіл канальних сигналів по фазі

Розглянемо множину сигналів

, , (9.15)

де   – коефіцієнти, що відображають передані повідомлення; – різниця фаз між сигналами сусідніх каналів.

Сигнали (9.15) розрізняються по фазі й, імовірно, можуть бути використані для побудови багатоканальної системи. Однак виявляється, що серед переносників вигляду

, , (9.16)

лише два будь-яких і можуть бути лінійно незалежними. Щоб переконатися в цьому, досить скористатися визначником Грама (9.11). Нехай , тобто

, . (9.17)

Тоді скалярні добутки ; = і, отже, для визначника Грама маємо [19]

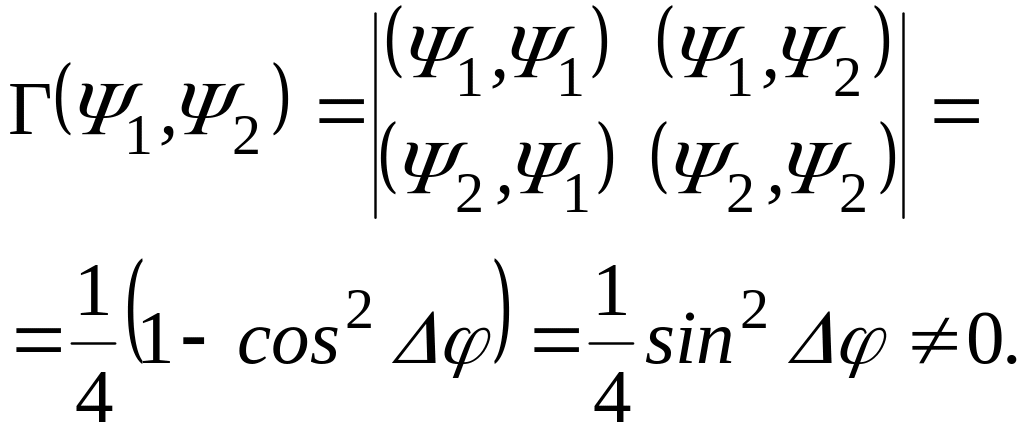(9.18)

З виразу (9.18) випливає, що при кожному або сигнали та можуть бути розділені. Цього не відбудеться при :

, ,

. (9.19)

Для скалярних добутків маємо наступне:

;

;

.

Підставивши значення скалярних добутків у визначник Грама для , одержимо

.

З множини сигналів, що розрізняються за фазою (9.15) лінійно незалежні тільки будь-які два сигнали. Тому на одній несучій частоті при довільних значеннях амплітуд і та фаз і можна забезпечити лише двоканальну передачу.

Повертаючись до визначника Грама для двох переносників і , знаходимо, що переносники із виразу (9.17) ортогональні при різниці фаз . Ортогональні переносники використовуються, зокрема, у квадратурній системі передач двох незалежних каналів.

9.5 Розподіл сигналів за формою

Загальною ознакою розподілу сигналів може служити форма сигналів. Сигнали, що розрізняються за формою, можуть передаватися одночасно, мати частотні спектри, які перекриваються, і проте такі сигнали можна розділити, якщо виконується умова їхньої лінійної незалежності або умова ортогональності.

Нехай переносниками обрані імпульси, послідовність яких утворює, наприклад, степеневий ряд

, . (9.20)

Для групового сигналу припустивши, що передана інформація міститься в коефіцієнтах , можна записати

, . (9.21)

Члени ряду (9.20) лінійно незалежні, і, отже, жоден з канальних сигналів не може бути утворений лінійними комбінаціями всіх інших сигналів. Це легко зрозуміти, звернувши увагу на те, що багаточлен вигляду (9.21) може бути тотожно рівним нулю тільки в тому випадку, коли всі його коефіцієнти дорівнюють нулю.

Для розподілу таких сигналів можна застосувати загальний метод відповідно до умови лінійної незалежності переносників (9.20). Так, при двоканальній передачі маємо для інтервалу

.

Якщо вагові функції в (9.7) вибрати так:

(9.22)

то в результаті операцій проектування вектора на напрямки координатних осей і одержимо (при ):

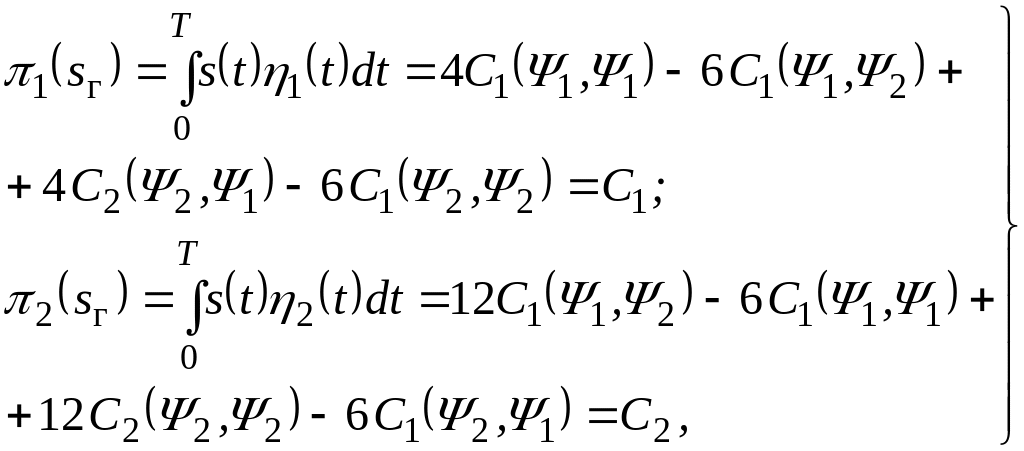(9.23)

де , , .

Операції (9.23) виконуються розподільним пристроєм, зображеним на рис. 9.8. На відміну від пристрою розподілу ортогональних сигналів тут додається пристрій формування вагових функцій і , котрі з функцій і утворюють лінійні комбінації вигляду (9.22). У загальному випадку використовується ітеративний метод ортогоналізації Грама-Шмідта, що полягає в побудові ортонормованої системи за заданою лінійно незалежною системою використовуючи допоміжні ортогональні вектори відповідно до співвідношення

,

де ,

Перестановка вихідних векторів приводить до різних ортонормованих систем , а через те, що процедура ітеративна її можна застосовувати для побудови як кінцевовимірних ортогональних базисів, так і рахункових ортонормованих систем у нескінченновимірних функціональних просторах .

При формуванні сигналів, що розрізняються за формою, як переносники застосовуються різні ортогональні функції, отримані на основі ортогоналізації степеневого ряду (9.20). Загальним недоліком отриманих у такий спосіб класичних поліномів є їхній континуальний характер, що пов’язано з необхідністю використання аналогової техніки для формування таких сигналів.

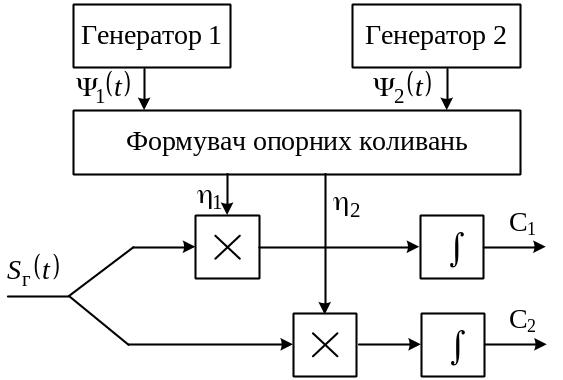
Рисунок 9.8 – Структурна схема лінійного розподілу сигналів за формою

Зовсім по-іншому формуються ортогональні сигнали на основі дискретних ортогональних послідовностей у вигляді функцій Уолша, Радемахера, що розглянуті в п. 2.3.

Через можливість застосування до функцій Уолша логічних операцій вони є досить перспективними при розробці багатоканальних цифрових систем передачі з розподілом за формою, а також в апаратурі формування й перетворення сигналів на базі мікропроцесорної техніки. У сучасній техніці багатоканального зв'язку при передачі дискретних повідомлень широке застосування знаходять системи з ортогональними індивідуальними сигналами, що перекриваються в часі та по частоті. Вони розподіляються в місці прийому за допомогою узгоджених пасивних фільтрів або еквівалентних їм активних кореляційних схем, забезпечуючи оптимальний прийом на фоні шуму.