9.3 Умова лінійного розподілу сигналів
Вплив
лінійного оператора
на функцію
можна представити у вигляді скалярного
добутку:
, (9.7)
де
– деяка вагова функція, що відповідає
операторові
.
Уперше визначення виборчих властивостей приймача (9.5) і (9.6) було запропоновано в 1935 р. Д.В. Агєєвим, він довів, що необхідною й достатньою умовою розподілу сигналів (9.2) за допомогою лінійних пристроїв є умова лінійної незалежності, яка визначається тотожністю [48]
(9.8)
і може виконуватися в тому єдиному випадку, коли всі коефіцієнти одночасно дорівнюють нулю.
Дійсно, відповідно до визначення виборчих властивостей (9.5) і (9.6) сигнали, які розподіляються і прийомні пристрої повинні задовольняти умові лінійного розподілу
,
, (9.9)
де
– відгук розподільного пристрою на
сигнал
,
причому при
,
і
.
Якщо застосувати оператор
до обох частин тотожності (9.8), то, беручи
до уваги (9.9) і принцип суперпозиції,
одержуємо
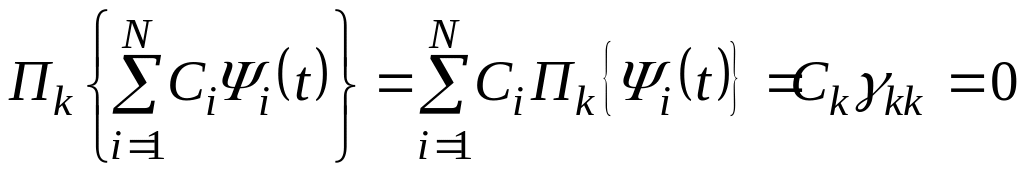. (9.10)
Але
значення
не дорівнюють тотожно нулю, отже,
дорівнюють нулю всі
для
.
Інакше кажучи, умова лінійного розподілу
(9.5) буде виконуватися лише тоді, коли
канальні сигнали лінійно незалежні.
Окремим випадком лінійно незалежних сигналів є ортогональні сигнали.
У загальному випадку необхідною й достатньою умовою лінійної незалежності ансамблю сигналів є відмінність від нуля визначника Грама; визначника, що наведений у вигляді матриці [42].
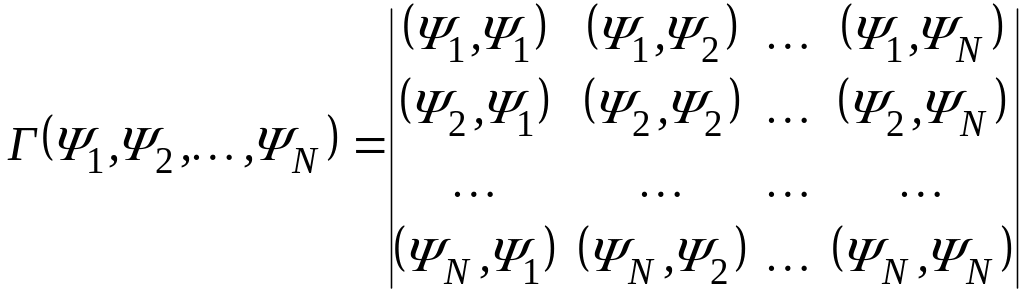, (9.11)
де
– скалярний добуток сигналів
та
.
Визначник
(9.11) дорівнює нулю, якщо функції (
,
,
…,
)
лінійно залежні, і більші від нуля для
лінійно незалежних функцій. Він дорівнює
добутку квадратів норм функцій
,
якщо вони попарно ортогональні.
Ортонормована система завжди лінійно
незалежна, для неї визначник Грама
дорівнює одиниці.
Нагадаємо,
що в
-мірному
евклідовому просторі, зокрема в просторі
сигналів, представлених усіченим рядом
Котельникова, коли
(
– база сигналу), можна вибрати не більше
лінійно незалежних сигналів. Вищевикладена
теорія лінійного розподілу побудована
без урахування адитивних завад у каналі.
У цих умовах теоретично байдуже, чи
вибирати систему переносників
ортогональних або просто лінійно
незалежних сигналів, у будь якому випадку
їх максимальна кількість не перевищує
бази сигналу
.
Однак, якщо врахувати вплив завад, то
перевага ортогональних сигналів стає
незаперечною, тому що тільки в цьому
випадку енергія сигналу використається
повністю. Окремим випадком ортогональних
сигналів є сигнали зі спектрами, що не
перекриваються, а також сигнали, що не
перекриваються в часі.
9.4 Основні способи розподілу сигналів
9.4.1 Частотний розподіл канальних сигналів
Розглянемо
основні етапи перетворення сигналів,
спектри яких займають смуги частот, що
не перекриваються, (рис. 9.2). Спочатку
відповідно до переданих повідомлень
первинні індивідуальні сигнали
,
,
…,
зі
спектрами
,
,
…,
модулюють
переносники - піднесучі частоти,
,
кожного каналу. Ця операція виконується
за допомогою модуляторів
,
,
…,
канальних
перетворювачів. Отримані на виході
частотних фільтрів
,
,
…,
спектри
канальних
сигналів займають відповідно смуги
частот
,
,
…,
,
які для спрощення будемо вважати рівними
ширині спектру повідомлень
(використовується односмугова модуляція).
Будемо вважати, що спектри повідомлень
фінітні.
Тоді
можна вибрати піднесучі частоти
,
так, що
смуги
,
…,
,
попарно
не перекриваються. При цьому умові
сигнали
взаємно
ортогональні. Спектри
,
,
…,
підсумовуються
в 1-му пристрої об'єднання сигналів, і
їхня сукупність
надходить
на 2-й груповий модулятор
.
Сумарна
смуга частот групового сигналу
.
У
груповому модуляторі спектр
за
допомогою коливання несучої частоти
переноситься
в область частот, відведену для передачі
даної групи каналів, у такий спосіб
груповий сигнал
перетвориться
в лінійний сигнал
.
При
цьому може використовуватися будь-який
вид модуляції, що забезпечує необхідну
завадостійкість передачі.
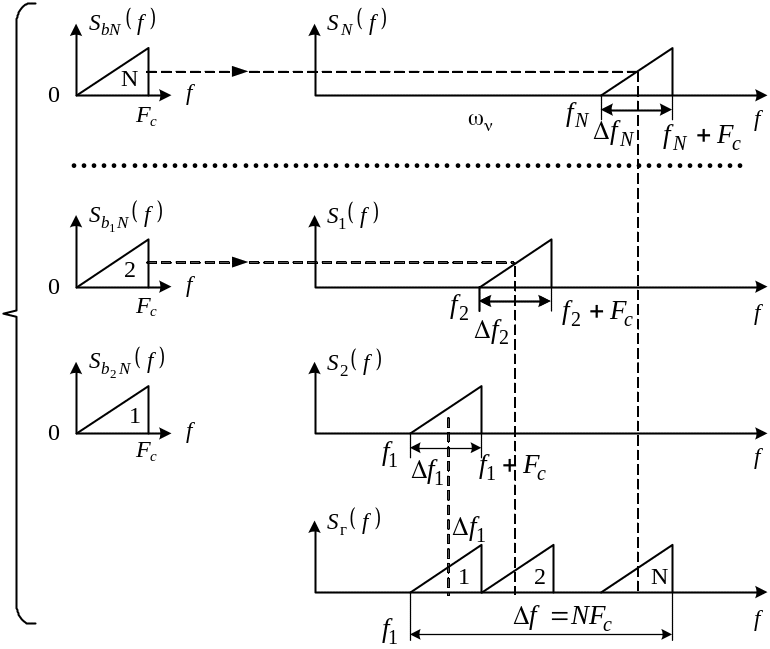
Рисунок 9.2 – Утворення спектра групового сигналу при багатоканальній передачі повідомлень з частотним розподілом каналів
На
приймальній стороні тракту лінійний
сигнал надходить на груповий демодулятор
(приймач
),
котрий
перетворює спектр лінійного сигналу в
спектр групового сигналу
.
Спектр
групового сигналу потім за допомогою
канальних приймачів
і
частотних фільтрів
,
що входять до них знову розділяється
на окремі смуги
й
потім за допомогою демодуляторів
перетворюється в спектри повідомлень
,
призначених одержувачам.
Для
того щоб без взаємних завад розподілити
сигнали при частотному розподілі, кожний
з фільтрів
повинен пропускати без ослаблення лише
ті частоти
,
які належать сигналу даного каналу;
частоти сигналів всіх інших каналів
фільтр
повинен послаблювати в певну кількість
разів.
Математично частотний розподіл ідеальними смуговими фільтрами (СФ) за аналогією з (9.7) можна представити виразом
,
(9.12)
де
–
імпульсна
характеристика ідеального смугового
фільтра, що пропускає без спотворень
сигнал із шириною спектра
.
Вираз
(9.12) збігається з (9.7) при ваговій функції
.
Згортці
(9.12) у частотній області відповідає
перемножування спектра групового
сигналу
на
–
подібну
передатну функцію
-го
фільтра (рис. 9.3).
Отже,
для ідеального виділення сигналів при
частотному розподілі необхідне виконання
двох умов: повне зосередження енергії
сигналів
у межах відведених смуг
та ідеальність характеристик СФ. Однак
жодна із цих умов принципово не здійсненна.
Рисунок 9.3 – Виділення сигналів окремих каналів за допомогою частотної фільтрації
Результатом
цього є взаємні завади при розподілі
сигналів. Для зниження взаємних перехідних
завад між каналами до припустимого
рівня доводиться вводити захисні
частотні інтервали
(рис. 9.4).
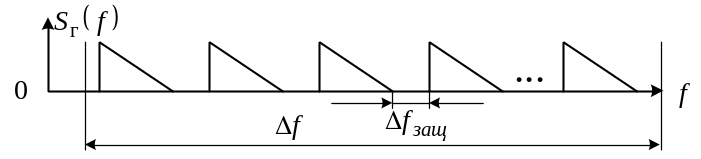
Рисунок 9.4 – Введення захисних частотних інтервалів розділових смугових фільтрів між окремими каналами
Так, у сучасних системах багатоканального телефонного зв'язку кожному каналу виділяється смуга частот 4 кГц, хоча частотний спектр переданих мовних сигналів обмежується смугою від 300 до 3400 Гц, тобто ширина спектра становить 3,1 кГц. Між смугами частот сусідніх каналів передбачені інтервали шириною по 0,9 кГц, призначені для зниження рівня взаємних завад при фільтруванні сигналів. Це означає, що в багатоканальних системах із частотним розподілом каналів (ЧРК) ефективно використовується лише близько 80 % смуги пропускання тракту передачі. Крім того, необхідно забезпечити дуже високий ступінь лінійності всього тракту групового сигналу, що є істотним недоліком способу ЧРК.