12. Визначення ідеальних координат зірок.
Відомо, що в фотографічному методі спостереження зображення зірок отримують на фотографії небесної сфери, яка є центральною проекцією відповідних зображень. За конструкцією фотоапарата фотоплівки розміщуються на відстані фокусної віддалі об’єктива. Довкруги оптичного центра фотокамери опишемо, радіусом що відповідає F,сферу і отримаємо на поверхні цієї сфери положення опорної зірки, полюса світу і головної точки об’єктива.
Приймемо, що екв коор A0 і D0 відомі. Нехай координати опорної зірки α і δ.
Знайдемо S
,
(2.34)
Спроектуймо на площину фотознімка методом центрального проектування полюс Р і цю точку проекції з’єднаємо з т Q0 , приймемо цей напрямок за вісь η системи прямокутних координат, в площині знімка проведемо перпендикулярно до η вісь ξ. Назвемо цю систему координат ξ η «ідеальною» системою координат в площині знімка. Тоді координати зірки будуть такими.
Відомо, що в центральних проекціях зберігається рівність кутів.
,
(2.35)
В (2.35) відоме тільки F.
Для визначення
розв’яжемо
сферичний трикутник
за трьома теоремами:
За теоремою косинусів
,
(2,36)
За теоремою синусів
,
(2,36)
За теоремою п’яти елементів
,
Щоб отримати величину
поділимо
третє рівняння (2,36) на перше рівняння
(2,36).
,
(2.37)
На основі (2,36) отримаємо вираз
для
.
Для цього друге рівняння (2.36) поділимо
на перше рівняння (2,36).
,
(2.38)
Для подальшого перетворення (2.37) і (2.38) зробимо наступну побудову.
Спроектуймо зображення зірки
на
сферичну дугу O`P
в т K.
Позначимо схилення т К через q.
За правилом Неппера знаходимо
,
(2.39)
Підставимо (2.39) в (2.37)
,
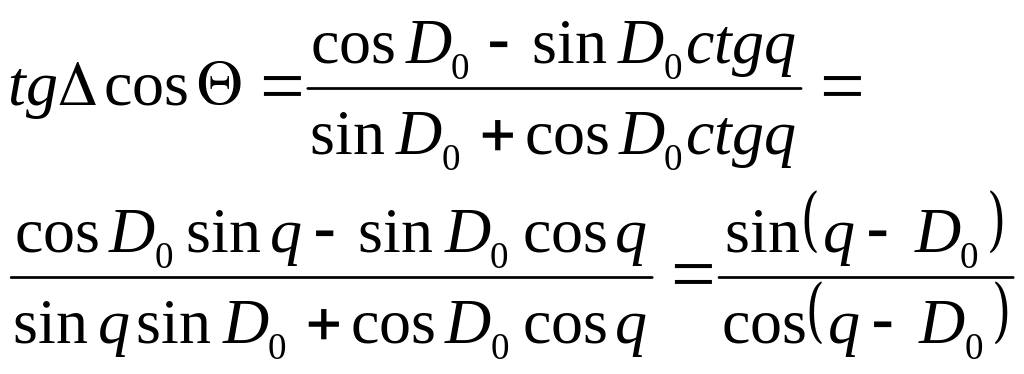
(2.40)
Підставимо (2.40) в (2.35)
,
(2.41)
Для подальшого перетворення (2.38) підставимо (2.39)
Представимо як
,
(2.42)
Підставимо (2.42) в друге рівняння (2.35)
,
(2.43)
– ідеальні координати.
13. Визначення екваторіальних координат супутника.
На основі виміряних координат опорних зірок і відомих значень ідеальних координат цих зірок складають для кожної зірки систему рівнянь Тернера.
,
(2.44)
В (2.44) a, b, c, d, e, f – коефіцієнти Тернера і в відповідності до теорії ці коефіцієнти для даного знімка є величинами постійними. Якщо рівнянь виду (2.44) скласти неменше 6, то з їх розв’язку можна визначити ці коф.
По зображеннях супутника на знімку вимірюють його прямокутні координати, знаючи кою Тернера для даного знімка складають рівняння виду (2.44) для супутника з розв’язку цих рівнянь визначиють ідеальні координати супутника.
,
(2.45)
Перевичислення ідеальних координат в екваторіальні
Знаходимо
:
,
(2.46)
На основі (2.35) і (2.38) запишемо:
Знаходимо
,
(2.48)
Якщо по (2.48) визначити пряме сходження і підставити це значення в (2.47), чи в (2.46), то можна обчислити схиляння.