7. Визначення координат точки спостереження з лазерних спостережень.

Відомо, що лазери дозволяють вимірювати відстань між точками спостереження. Якщо такою точкою є супутник координати якого відомі на момент спостереження, то визначивши відстань до супутника отримаємо можливість скласти рівняння виду.

, (2.22)

В (2.22) невідомі є координати точки спостережень . Треба мати мінімум три рівняння виду (2.22) – це означає що в лазерному методі необхідно спостерігати мінімум в трьох точках супутник, при чому координати супутника в цих точках спостереження повинні бути відомими на момент спостереження.

8. Визначення координат точки спостереження з комбінованих спостережень.

Фотографічний і лазерний. Відомо, що застосування фотографічного методу для спостережень супутника отримаємо можливість визначити координати супутника на момент спостереження. Одночасна застосування лазерного методу дозволяє визначити відстань до супутника на момент спостереження. Якщо в момент спостереження супутника його координати були відомі, то отримаємо можливість отримати координати точку спостережень з рівняння (2.18):

, (2.26)

Де

Фотографічний і допплерівський метод. Приймемо, що супутник спостерігається в т С₁ і С₂ і С₃ і координати супутника в цих точках є відомими. В т С₁ спостереження виконано фотографічним методом, а т С₂ і С₃ використовували допплерівський метод спостереження, який дозволяє визначити різницю відстаней до супутника. З обробки результатів спостереження фотографічним методом визначили екваторіальні координати супутника в т С₁, що дозволяє обчислити напрямні косинуси вектора R₁:

, (2.28)

Оскільки координати супутника в т С відомі, то за цими координатами можна обчислити відстань між т С₁ і С₂, С₂ і С₃

, (2.29)

За відомою відстанню і координатами т С₁ і С₂ можна обчислити напрямні косинуси вектора .

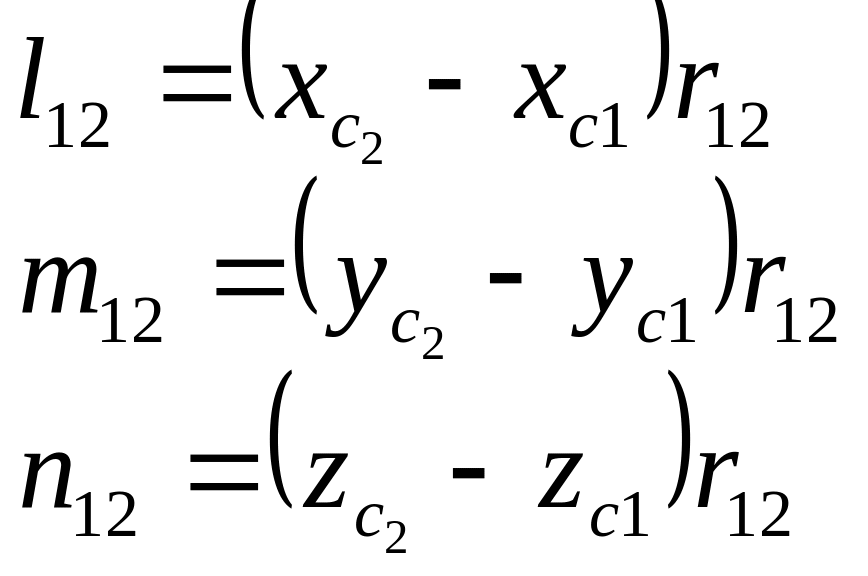, (2.30)

Знаючи напрямні косинуси векторів визначають величину плоского кота в вершині С₁

, (2.31)

Визначивши цей кут можна скласти рівняння для визначення відстані

, (2.32)

Аналогічно знаходимо відстань , попередньо обчисливши за формулою аналогічною до (2.31) косинуси кута при вершині С₁ в цьому трикутнику.

, (2.33)

З (2.33), (2.32), (2.27) отримаємо три рівняння з трьома невідомими , , , розв’язуючи ці рівняння знаходимо відповідні відстані, а потім за формулами (2.26) з врахуванням (2.28) визначаємо координати точки спостереження Q.

9. Визначення координат точок Земної поверхні із спостереження супутників системи gps.

GPS метод є радіотехнічним методом спостереження. Супутники, що входять в систему GPS, об лаштовані атомними годинниками, генераторами частоти, пристроями передачі і приймання електромагнітних коливань, які працюють в так званому L-діапазоні.

Нехай зі супутника передається сигнал точного часу в момент t_S, а в момент t_R ці сигнали приймаються в пункті спостереження. Нехай поправки сигналів передач і приймання є відповідно , тоді відстань від супутника до точки спостереження може бути визначена з формули:

,

де с – швидкість світла, – різниця часу.

, (2.23)

Підставляючи (2.23) в формулу відстані:

R може бути визначений з виразу

, (2.24)

Тоді

, (2.25)

Аналізуючи (2.25) бачимо, що в цьому рівнянні є чотири невідомі величини і зсув годинника в точці спостереження . Для визначення невідомих величин необхідно скласти як мінімум чотири рівняння виду (2.25), а це означає що з пункту спостережень необхідно спостерігати мінімум чотири супутники, координати яких а момент спостереження повинні бути відомими.