3. Расчет облучателя и его дн.

Облучатель зеркальной антенны является важнейшим её элементом, во многом определяющим характеристики антенны в целом. Он должен удовлетворять следующим основным требованиям:

1. Иметь ДН, обеспечивающую надлежащее облучение зеркала и имеющую минимальный уровень боковых лепестков.

2. Иметь минимальные размеры.

3. Иметь фазовый центр.

4. Пропускать без пробоя заданную мощность.

5. Иметь требуемую диапазонность.

6. Иметь небольшой вес и достаточную механическую прочность креплений.

7. Обеспечивать необходимую стойкость к воздействию метеоусловий и возможность полной герметизации фидерного тракта.

Исходя из этих требований, будем определять конструкцию облучателя. Требования 4, 5 мы уже выполнили, выбрав фидерный тракт, конец которого является облучателем.

ДН открытого конца круглого волновода или конического рупора (если фазовые ошибки в раскрыве рупора не очень велики) приближенно рассчитывается по формулам [1,с.507,522]:

в плоскости E

;

в плоскости Н

,

где - коэффициент распространения волны в волноводе, , - коэффициент отражения от открытого конца волновода. На практике приближенно определяют соотношением:

Используя программный пакет Mathcad 2000 Professional, по приведенным формулам (см.приложение 4.1) построил ДН для открытого конца круглого волновода (рис.7).

Как видно из рисунка, данный облучатель имеет большой уровень боковых лепестков и его ДН сильно отличается в Е- и Н-плоскотях, поэтому такой облучатель не подходит.

В данном случае видна прямая необходимость в коническом рупоре. Используя всё те же формулы методом подбора определил такой радиус раскрыва рупора , при котором ДН имеет малый уровень боковых лепестков, незначительно отличается в Е- и Н-плоскотях и довольно широкая (рис.8). При этом используемые формулы не учитывают фазовых погрешностей в раскрыве рупора. Ими можно пренебречь в том случае, если при заданном длина рупора значительно больше (оптимальной длины рупора). Таким образом, подобрав , можно утверждать, что рассчитанная ДН будет близка к реальной. Размеры оптимального рупора связаны соотношением [1,с.522]:

.

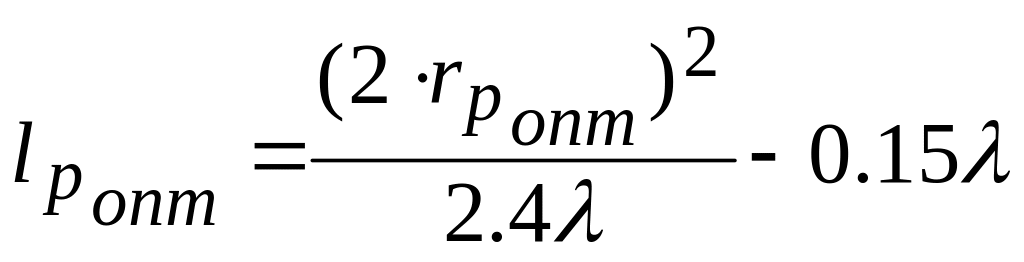Приняв , найдем: .

В результате выбираем , при этом величина максимальной фазовой ошибки составит [1,с.525]:

.

Для упрощения дальнейших вычислений будем считать, что ДН рупора имеет форму тела вращения, и аппроксимируем её функцией [5,с.319]:

.

очень близка к рассчитанным (см.рис.9). В этом случае коэффициент направленного действия (КНД) облучателя равен [5,с.319]:

,

где - степень аппроксимирующей функции.

В итоге размеры облучателя будут иметь значения, показанные на рис.10.

4. Расчет размеров зеркала и дн параболической антенны.

Расчёт параболической антенны будем производить апертурным методом. Плотность потока излучения в апертуре равна плотности потока излучения в соответствующей точке зеркала, так как между зеркалом и апертурой лучи параллельны. Поэтому по ДН облучателя можно найти нормированное амплитудное распределение в раскрыве по следующим формулам [3,с.436] (см.рис.3):

Сделаем дополнительные преобразования:

.

Выразим через , (радиус зеркала) и :

.

В итоге, подставив и , получим:

Теперь определимся с . В целях получения лучших характеристик антенны (малые размеры и себестоимость, большее усиление) найдем оптимальный угол раскрыва , при котором коэффициент использования поверхности (КИП), а, следовательно, КНД максимальны. Приняв , получим по максимуму функции [5,с.319]:

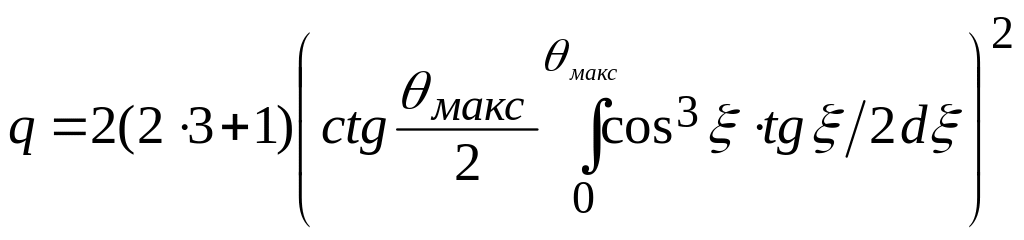
Используя Mathcad, построил график функции и по нему определил (рис.11) (см.приложение 4.2).

Зная и задавая значение , можно найти нормированное распределение амплитуды по раскрыву, которое затем аппроксимируется формулой [4,с.437]:

.

Подобрав значения и , ДН зеркальной антенны находят по формуле [4,с.305]:

,

где - угловая переменная, - лямбда-функции, которые просто связаны с обычными функциями Бесселя:

.

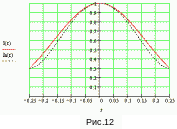Набрав все необходимые формулы в Mathcad (см.приложение 4.3), методом подбора нашёл такое , при котором ширина главного лепестка на уровне половинной мощности , уровень боковых лепестков . При этом старался добиться минимальных размеров зеркала по экономическим соображениям. В результате получил радиус зеркала . При таком значении нормированное распределение амплитуды по раскрыву показано на рис.12. Подобрав значения и , аппроксимировал его функцией (рис.12):

Как видно из рис.12, хорошо приближается к . Отсюда получаем выражение для ДН антенны:

,

где , , .

Нормированная ДН параболической антенны приведена на рис.13. Поскольку ДН облучателя обладает симметрией вращения относительно оси зеркала и зеркало представляет собой параболоид вращения, то ДН антенны в Е- и Н-плоскостях будут одинаковыми (рис.13).

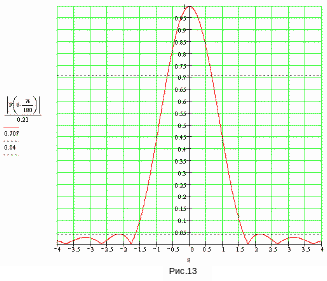
По полученной ДН находим ширину главного лепестка на уровне половинной мощности , уровень боковых лепестков :

; .

Данные значения полностью удовлетворяют техническому заданию.

Ф окусное расстояние антенны рассчитывается по формуле [1,с.537]:

.

Так как ДН облучателя имеет незначительный задний лепесток, то корректировку фокусного расстояния проводить не будем [1,с.547] (хотя полученное значение фокусного расстояния и так получилось соответствующим корректированному ).

Форма параболического отражателя определяется выражением:

.

В итоге получаем следующие размеры зеркала (рис.14).