1.3.2. Определение усилий в стойках рамы

При определении усилий рассматривается поперечный ряд колонн (стоек), соединенных шарнирно с фермой и жестко защемленных в уровне обреза фундамента. Стропильные балки фермы являются ригелями рамы, которые ввиду большой продольной жесткости создают равные перемещения всех стоек рамы при любых воздействиях внешней нагрузки.

Расчетная схема рамы приведена на рис. 2.5. Для каждого вида загружения (рис. 2.6) составляется каноническое уравнение метода перемещений, из которого находится величина перемещения , после чего определяется значение упругой реакции на уровне верха каждой стойки по формуле (13).

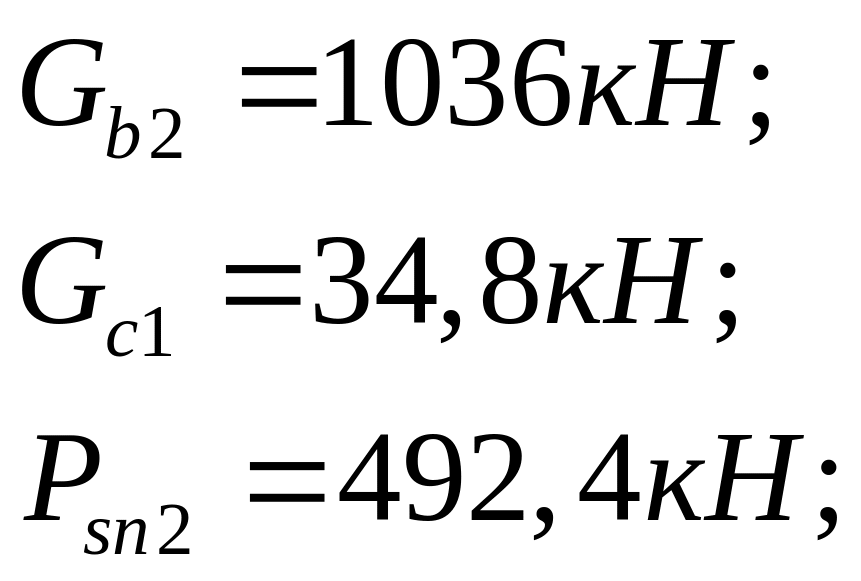
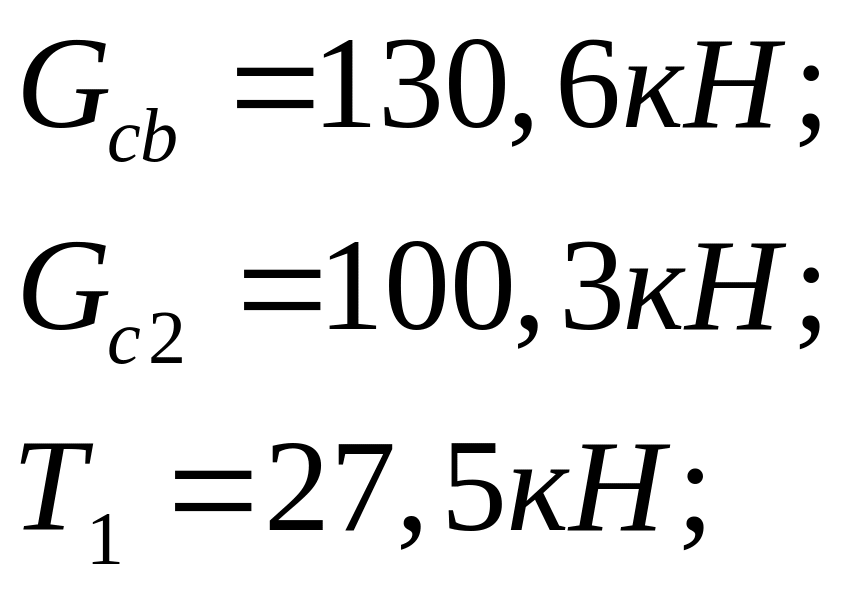
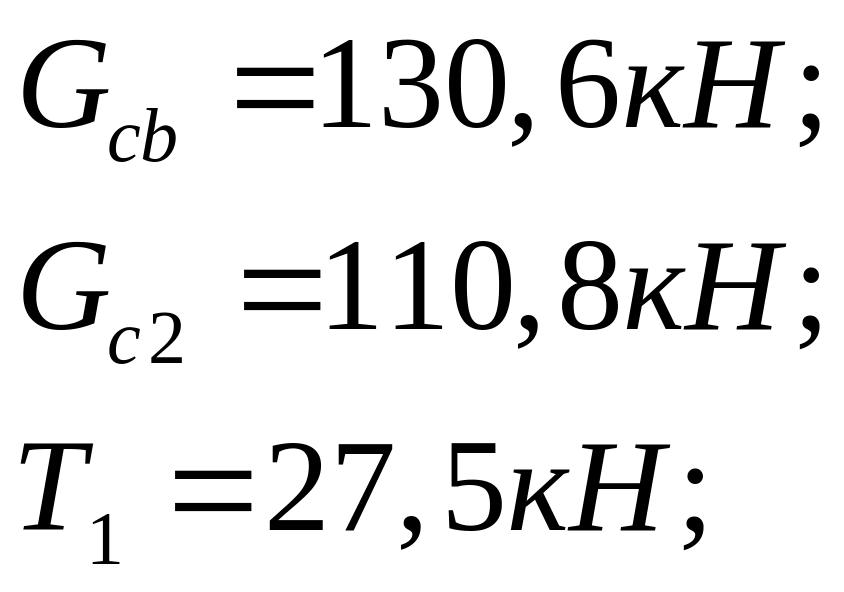
кН; кН/м; кН/м; N_max = 825,4 кН; N_min = 248,9 кН.

Рис. 2.5. Схема приложения нагрузок и расчетная схема поперечной рамы

По длине колонны принимаются четыре расчетных сечения (рис. 2.9): I-I у верха колонны; II-II – непосредственно над крановой консолью; III-III – непосредственно под крановой консолью; IV-IV – у верхнего обреза фундамента.

При расчете рамы принимаем следующие правила знаков: силовая реакция, направленная вправо, положительна; изгибающий момент, вызывающий растягивающие усилия в левых волокнах стоек, положительный; поперечная сила положительна, если она будет вращать стойки у заделки с однозначной эпюрой изгибающего момента.

Рис. 2.6. Схема усилий в стойках рамы при некоторых загружениях

Определение реакций верха колонн от единичного смещения ₁ = 1 и от каждого вида нагрузки (рис. 2.6) выполняется по прил. 3.

Определение реакций верха колонн от единичного смещения ₁ = 1

Для колонны крайнего ряда (см. рис. 2.3, 2.5) по формуле (1) прил. 3

;

;

;

;

.

Считая условно, что жесткость надкрановой части колонны , будем иметь приведенную жесткость подкрановой части , поскольку .

Реакция , условно уменьшенная в раз, будет

.

Для колонны среднего ряда реакция В_Δ от смещения Δ₁= 1 опреде­ляется так же, но значение коэффициента χ вычисляется по формуле (7) прил. 3

.

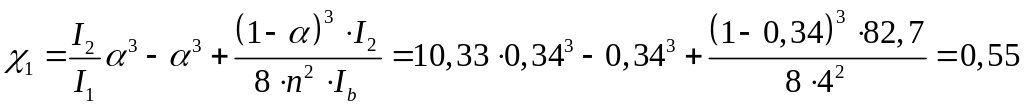Здесь п = 4 – число панелей двухветвевого участка колонны; I_b – момент инерции сечения отдельной ветви.

Для колонны среднего ряда (см. рис. 2.3) ширина сечения колонны b = 50 см, высота сечения ветвей h = 30 см, расстояние в свету между ветвями с₁ = 80 см (h₂ - 2h = 140 - 2· 30 = 80).

Момент инерции сечения подкрановой части относительно оси ко­лонны

;

;

;

;

.

Жесткость сечения подкрановой части двухветвевой колонны, при­веденная к жесткости сечения надкрановой части колонны крайнего ряда

.

Реакция верха колонны среднего ряда, уменьшенная в Е_ь1₂ раз, определяется по следующей формуле

.

Суммарная реакция

.

С учетом пространственной работы каркаса здания при действии крановых нагрузок

.

Определение расчетных усилий в сечениях колонн от постоянной и временной нагрузок

Схема приложения вертикальных нагрузок на колонны приведена на рис. 2.7.

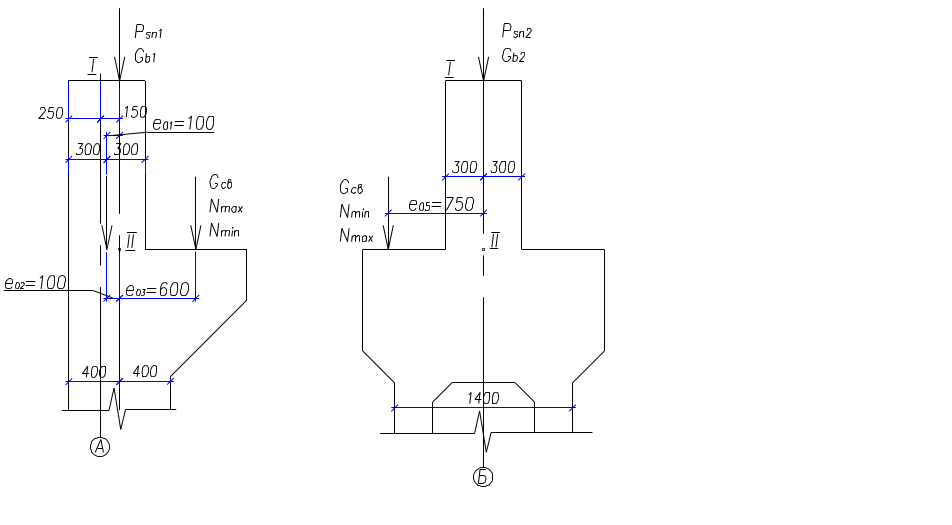Рис. 2.7. Схема приложения вертикальных нагрузок:

а – на колонну по оси А; б – на колонну по оси Б

Расчетные усилия от постоянной нагрузки

Изгибающий момент от внецентренного приложения постоянной нагрузки в колонне крайнего ряда (по оси А) в точке I (см. рис. 2.7)

кНм,

то же в точке II

кНм.

В колонне среднего ряда (по оси Б) изгибающие моменты от постоянной и снеговой нагрузок не возникают вследствие симметричности поперечной рамы.

Упругие реакции на уровне верха колонн

1. От изгибающего момента кНм.

Для колонны по оси А реакция верхнего конца колонны сплошного сечения определяется по формуле (2) прил. 3

Для колонны по оси Б кН. Суммарная реакция связей в основной системе .

.

Окончательно из уравнения упругая реакция кН, где знак «–» для колонны по оси А, а знак «+» для колонны по оси В.

2. От изгибающего момента кНм.

Реакция верхнего конца колонны по осям А и В определяется по формуле (3) прил. 3

кН.

Для колонны по оси В кН.

Упругая реакция кН. Суммарная упругая реакция верха крайней колонны от воздействия и

кН.

Расчетные усилия от постоянной нагрузки (см. рис. 2.5) в сечениях колонны по оси А:

кНм;

кНм;

кНм;

кНм;

кН;

кН;

кН;

кН;

кН (для всех сечений колонны);

в сечениях колонны по оси Б:

;

;

;

;

;

.

Эпюры изгибающих моментов при различных видах загружения строим в табл. 2.3 расчетных усилий.