Линейная алгебра
Контрольная работа по аналитической геометрии на плоскости.
Вариант 1
Пусть А (-1, 3), В (2, 11), С (5, -13) - вершины треугольника АВС. Найти:
а) уравнение стороны ВС; б) уравнение медианы АМ; в) уравнение биссектрисы АД; г) уравнение высоты АН; д) площадь треугольника АВС.
Составить уравнение линии, расстояние от каждой точки которой до точки А (5, 9) в два раза меньше расстояния до прямой x = 2.
Дано уравнение кривой второго порядка:
.
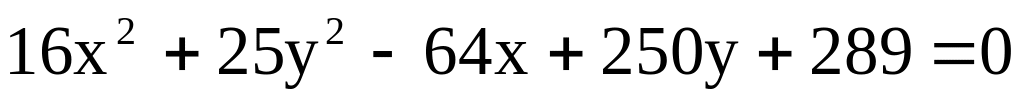а) привести уравнение к каноническому виду;
б) определить тип кривой, полуоси, эксцентриситет;
в) найти расстояние от центра кривой до прямой 3x – 4y + 5 = 0;
г) построить кривую.
Вариант 2
Пусть А (1, 1), В (7, 4), С (4, 5) - вершины треугольника АВС. Найти:
а) уравнение стороны ВС; б) уравнение медианы АМ; в) уравнение биссектрисы АД; г) уравнение высоты АН; д) площадь треугольника АВС.
Составить уравнение линии, расстояние от каждой точки которой до точки А (-1, -2) равно расстоянию до прямой x = -3.
Дано уравнение кривой второго порядка:
.
а) привести уравнение к каноническому виду;
б) определить тип кривой, полуоси, эксцентриситет;
в) найти расстояние от центра кривой до прямой x + y + 5 = 0;
г) построить кривую.
Вариант 3
Пусть А (1, 1), В (-5, 4), С (-2, 5) - вершины треугольника АВС. Найти:
а) уравнение стороны ВС; б) уравнение медианы АМ; в) уравнение биссектрисы АД; г) уравнение высоты АН; д) площадь треугольника АВС.
Составить уравнение линии, для каждой точки которой отношение расстояний до точки А (7, 0) и прямой x = 1 равно
.Дано уравнение кривой второго порядка: .
а) привести уравнение к каноническому виду;
б) определить тип кривой, полуоси, эксцентриситет;
в) найти расстояние от центра кривой до прямой 3x – y + 12 = 0;
г) построить кривую.
Вариант 4
Пусть А (-1, 1), В (5, 4), С (2, 5) - вершины треугольника АВС. Найти:
а) уравнение стороны ВС; б) уравнение медианы АМ; в) уравнение биссектрисы АД; г) уравнение высоты АН; д) площадь треугольника АВС.
Составить уравнение линии, для каждой точки которой отношение расстояний до точки А (2, 0) и прямой x = 4 равно
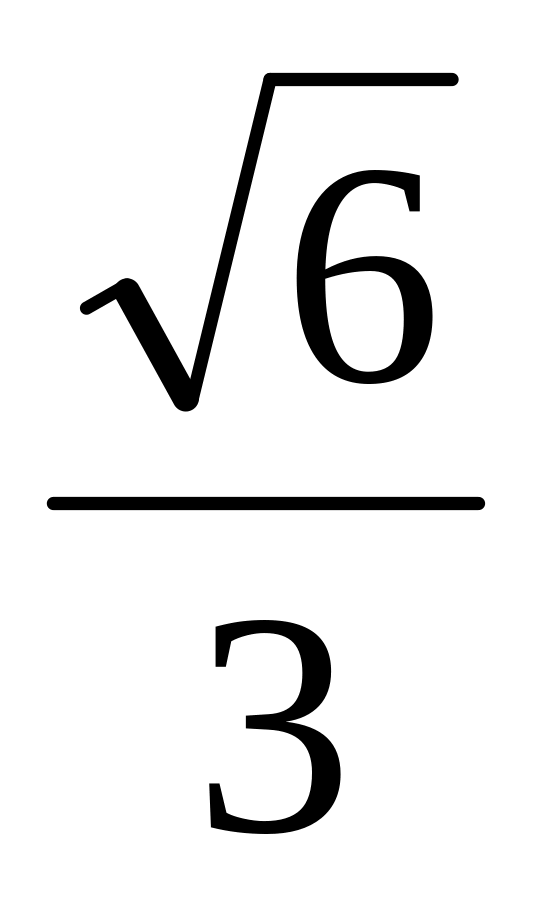.Дано уравнение кривой второго порядка: .
а) привести уравнение к каноническому виду;
б) определить тип кривой, полуоси, эксцентриситет;
в) найти расстояние от центра кривой до прямой 2x + 4y - 6 = 0;
г) построить кривую.
Вариант 5
Пусть А (-1, 1), В (-7, 4), С (-4, 5) - вершины треугольника АВС. Найти:
а) уравнение стороны ВС; б) уравнение медианы АМ; в) уравнение биссектрисы АД; г) уравнение высоты АН; д) площадь треугольника АВС.
Составить уравнение линии, расстояние от каждой точки которой до точки А (3, 3) равно расстоянию до прямой y = -2.
Дано уравнение кривой второго порядка:
.
а) привести уравнение к каноническому виду;
б) определить тип кривой, полуоси, эксцентриситет;
в) найти расстояние от центра кривой до прямой x – y + 4 = 0;
г) построить кривую.
Вариант 6
Пусть А (1, -1), В (-5, 2), С (-2, 3) - вершины треугольника АВС. Найти:
а) уравнение стороны ВС; б) уравнение медианы АМ; в) уравнение биссектрисы АД; г) уравнение высоты АН; д) площадь треугольника АВС.
Составить уравнение линии, для каждой точки которой отношение расстояний до точки А (2, 0) и прямой x = ½ рано 2.
Дано уравнение кривой второго порядка:
.
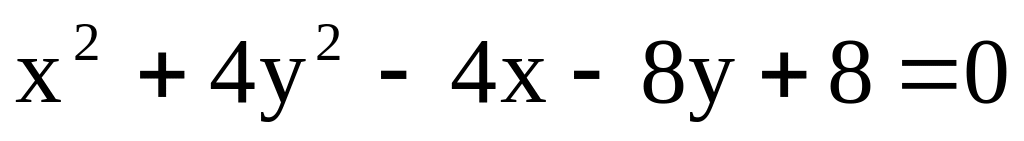а) привести уравнение к каноническому виду;
б) определить тип кривой, полуоси, эксцентриситет;
в) найти расстояние от центра кривой до прямой 3x – 4y + 5 = 0;
г) построить кривую.
Вариант 7
Пусть А (-1, -1), В (5, 2), С (2, 3) - вершины треугольника АВС. Найти:
а) уравнение стороны ВС; б) уравнение медианы АМ; в) уравнение биссектрисы АД; г) уравнение высоты АН; д) площадь треугольника АВС.