
- •Часть 3. Оптика. Атомная и ядерная физика
- •3.1. Основные формулы и законы оптики
- •3.1.1. Волновая оптика
- •3.1.2. Поляризация света
- •Контрольное задание №5 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •3.2. Основные формулы и законы теплового излучения, атомной и ядерной физики
- •3.2.1. Тепловое излучение
- •3.2.2. Атомная физика
- •3.2.3. Ядерная физика
- •Контрольное задание №6 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •3. Некоторые внесистемные величины:
- •4. Основные физические постоянные:
- •7. Молярные массы (м 10-3 кг/моль) газов:
- •8. Основные физические величины
- •Библиографический список
- •Общая физика Контрольные задания для студентов специалистов разных специальностей
- •660041, Г. Красноярск, пр. Свободный, 79
- •660041, Г. Красноярск, пр. Свободный, 82а
Часть 3. Оптика. Атомная и ядерная физика
Задачи, приведенные в контрольных работах, соответствуют программе общего курса физики в техническом вузе и охватывают разделы «Волновая оптика», «Тепловое излучение», «Атомная физика» и «Ядерная физика».
В работе отсутствуют сведения, которые при необходимости могут быть найдены в учебных пособиях по курсу общей физики (см. библиографический список). Поэтому вначале помещен краткий перечень формул и законов, необходимых для решения задач.
В приложении приведены основные справочные данные, дополняющие условия задач. Номера вариантов, которые должен выполнить студент, указывает преподаватель.
3.1. Основные формулы и законы оптики
3.1.1. Волновая оптика
Абсолютный
показатель преломления среды:
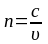 ,
,
где
 и
и
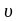 - скорости электромагнитных волн (света)
в вакууме и среде.
- скорости электромагнитных волн (света)
в вакууме и среде.
Закон
преломления света на границе раздела
двух сред с абсолютными показателями
преломления
 и
и
 :
:
 ,
,
где
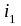 -
угол падения,
-
угол падения,
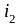 -
угол преломления луча света;
-
угол преломления луча света;
 - относительный показатель преломления
двух сред.
- относительный показатель преломления
двух сред.
Полное
отражение наблюдается при падении
света из среды оптически более плотной
(
)
в среду оптически менее плотную (
),
т.е. при
>
.
В этом случае угол преломления
 и
и
 :
:
 и
и
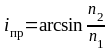 ,
,
где
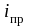 -
предельный угол полного отражения
света; при угле падения
>
свет полностью отражается от границы
раздела сред.
-
предельный угол полного отражения
света; при угле падения
>
свет полностью отражается от границы
раздела сред.
Формула
тонкой собирающей линзы:
 ,
,
где
 -
фокусное расстояние линзы;
-
фокусное расстояние линзы;
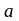 -
расстояние от предмета до оптического
центра линзы;
-
расстояние от предмета до оптического
центра линзы;
 -
расстояние от оптического центра линзы
до изображения предмета. Для тонкой
рассеивающей линзы расстояния
и
считаются отрицательными.
-
расстояние от оптического центра линзы
до изображения предмета. Для тонкой
рассеивающей линзы расстояния
и
считаются отрицательными.
Оптическая
сила линзы:
 .
.
Оптическая
длина пути световой волны:
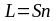 ,
,
где
 - геометрический путь световой волны;
- геометрический путь световой волны;
 -
абсолютный показатель преломления
среды.
-
абсолютный показатель преломления
среды.
Оптическая
разность хода двух когерентных световых
волн:
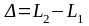 ,
,
где
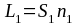 и
и
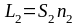 - оптические пути световых волн в первой
и во второй средах.
- оптические пути световых волн в первой
и во второй средах.
Разность фаз колебаний векторов напряженностей электрического поля (световых векторов) двух когерентных световых волн:
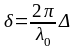 ,
,
где
 -
длина этих волн в вакууме.
-
длина этих волн в вакууме.
Условия максимумов интенсивности света при интерференции:
 и
и
 ,
где
,
где
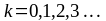
Условия минимумов интенсивности света при интерференции:
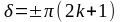 и
и
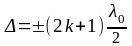 ,
где
,
где
Координаты максимумов и минимумов интенсивностей света в интерференционной картине, полученной от двух когерентных источников:
 и
и
 ,
,
где
 - расстояние от источников света до
экрана;
- расстояние от источников света до
экрана;
 -
расстояние между источниками света;
-
расстояние между источниками света;
Ширина
интерференционной полосы:
 .
.
Оптическая
разность хода двух световых волн,
отраженных от верхней и нижней поверхностей
плоскопараллельной тонкой пленки,
находящейся в воздухе с абсолютным
показателем преломления
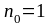 :
:
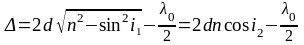 ,
,
где - толщина пленки; - абсолютный показатель преломления пленки;
-
длина световых волн в воздухе (вакууме);
и
-
углы, соответственно, падения и преломления
света. Второе слагаемое в этих формулах
учитывает увеличение оптической длины
пути световой волны на
 при отражении ее от среды оптически
более плотной (
>
при отражении ее от среды оптически
более плотной (
>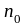 ).
).
Радиусы светлых колец Ньютона в отраженном свете (темных колец в проходящем свете):
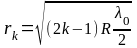 при
при
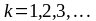
и радиусы темных колец Ньютона в отраженном свете (светлых колец в проходящем свете):
 при
при
где
 -
радиус кривизны линзы;
-
длина световой волны в воздухе (вакууме),
находящемся между линзой и стеклянной
пластинкой.
-
радиус кривизны линзы;
-
длина световой волны в воздухе (вакууме),
находящемся между линзой и стеклянной
пластинкой.
Радиусы зон Френеля, построенных на сферической волновой поверхности:
 при
,
при
,
где - радиус сферической волновой поверхности точечного источника света; - расстояние от волновой поверхности до точки наблюдения;
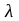 -
длина световой волны в данной среде.
-
длина световой волны в данной среде.
Дифракция Фраунгофера на одной щели:
а)
условие максимумов интенсивности света
 ;
;
б)
условие минимумов интенсивности света
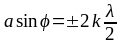 ,
,
где
- ширина щели;
 - угол дифракции, определяющий направление
максимума или минимума интенсивности
света;
- длина световой волны в данной среде;
- угол дифракции, определяющий направление
максимума или минимума интенсивности
света;
- длина световой волны в данной среде;
При
падении параллельного пучка света на
щель под углом
 условие дифракционных максимумов имеет
вид:
условие дифракционных максимумов имеет
вид:
 .
.
Дифракция Фраунгофера на дифракционной решетке:
а) условие главных минимумов интенсивности света
при ;
б) условие дополнительных минимумов интенсивности света
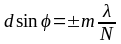 при
при
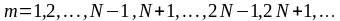 (
( );
);
в) условие главных максимумов интенсивности света
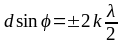 при
при
 ,
,
где
-
ширина одной щели;
-
постоянная решетки;
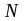 -
общее число щелей;
- угол дифракции, определяющий направление
максимума или минимума интенсивности
света;
-
длина световой волны в данной среде;
-
общее число щелей;
- угол дифракции, определяющий направление
максимума или минимума интенсивности
света;
-
длина световой волны в данной среде;
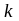 -
порядок спектра.
-
порядок спектра.
При
падении параллельного пучка света на
дифракционную решетку под углом
условие главных максимумов имеет вид:
 .
.
Разрешающая способность дифракционной решетки:
 ,
,
где
и
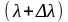 -
длины двух световых волн, еще разрешаемых
решеткой по критерию Рэлея;
-
общее число щелей;
- порядок спектра.
-
длины двух световых волн, еще разрешаемых
решеткой по критерию Рэлея;
-
общее число щелей;
- порядок спектра.
При дифракции рентгеновских лучей на кристаллической решетке направления максимальных интенсивностей этих лучей определяются по формуле Вульфа-Брэггов:
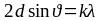 при
,
при
,
где
-
расстояние между параллельными
кристаллографическими плоскостями;
-
длина волн рентгеновских лучей;
 -
угол скольжения рентгеновских лучей.
-
угол скольжения рентгеновских лучей.
