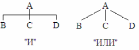Предикатная модель представления знаний.
Для представления математических знаний в математической логике давно используют исчисление предикатов, которое имеет формальную семантику и для него разработаны механизмы вывода. Поэтому исчисление предикатов было исторически первым логическим языком, который применим для формального описания предметных областей в СИИ. Однако логике предикатов, как и продукционной модели присущи такие недостатки как:
чрезмерный уровень формализации представленных знаний;
трудность их прочтения;
слабая производительность обработки знаний из-за того что все отношения описываются предикатами, а это не очень согласуется со структурами данных, принятыми для компьютерной обработки.
Допустимые выражения логики предикатов называются правильно построенной формой (ППФ). Элементарными компонентами языка исчисления предикатов являются:
предикатные символы;
символы переменных;
символы констант;
функциональные символы.
Используют комбинации этих элементарных компонентов. С учётом синтаксиса формы можно построить различные предикатные атомарные формулы.
читать А(кто читает) В(что читает)
А читает В читать(А,В), здесь А-символ, В-переменная
А читает книгу читать(А,«книга»), здесь читать - предикатный символ, «книга»-символ константы,
В конкретной области ППФ имеют свою интерпретацию. Предикатному символу приписывается соответствующее отношение этой предметной области. Каждому символу констант приписывается элемент этой предметной области. Каждому функциональному элементу функция этой предметной области. Как только интерпретация формулы для которой предметные области определены, можно сказать, что формула имеет значение истина в том случае, когда соответствующее утверждение об области обсуждения истинно, в противном случае формула принимает значение ложь. Атомарные формулы можно комбинировать для образования более сложных ППФ, для этого используются логические связи И, ИЛИ, НЕ и импликация.
А живёт в кирпичном доме.
жить(А,«дом»)
материал(«дом»,«кирпичный»).
А играет в центре поля или у сетки.
играть(А,«в центре») V играть(А,«у сетки»).
Мышь не сочиняет стихи.
сочинять(«мышь»,«стих»).
Если у кого-то есть собака, значит, он любит животных.
владеть(А,«собака») => любить(А,«животные»).
Также используются кванторы:
квантор общности КА(х);
Все читают книги.
(КА(х)) читать (х,«книги»). – для всех х следующих за квантором общности, формула является истиной.
квантор существования Е(х);
Существует кто-то, кто читает книги.
(Е(х)) читать (х,«книги»).
Если некоторая переменная ППФ проквантифицирована, то говорят, что она называется связанной переменной. В противном случае она называется свободной.
Редукционная модель представления знаний.
Предикатные и продукционные модели хотя и являются достаточно универсальными, но при их применимости процедура обработки знаний очень неэффективна из-за того, что каждый раз просматривается весь перечень продукции или предикатов.
Редукционные модели представляют собой гибрид системы продукций с И-ИЛИ графами. В виде И-ИЛИ графа задаётся взаимосвязь продукций и за счёт этого в процессе обработки удаётся отсечь заведомо ненужные продукции.
