1.4 Смешанные стратегии

Смешанной стратегией (с.с.) игрока в матричной игре называется вероятностное распределение на множестве его ч.с. Таким образом, если i=1,…,m – чистые стратегии игрока I, а j=1,…,n – чистые стратегии игрока II, то с.с. игрока I – это вероятностный вектор , где – вероятность выбора игроком I чистой стратегии i, i=1,…,m. Очевидно, что вектор x должен удовлетворять условиям:

. (1.1)

Аналогично с.с. игрока II – это вероятностный вектор , удовлетворяющий условиям

. (1.2)

Обозначим множество всех с.с. игрока I через X, а игрока II – через Y. Если I выбрал с.с. , а II – , то выигрышем игрока I (соответственно, проигрышем игрока II) в ситуации (x,y) естественно считать математическое ожидание

. (1.3)

В соответствии с принципом минимакса гарантированный, то есть наименьший выигрыш игрока I при выборе им с.с. x будет

. (1.4)

Поэтому игроку I выгодно выбрать x так, чтобы максимально увеличить u(x):

. (1.5)

Аналогично гарантированный, то есть наибольший, проигрыш игрока II при выборе им с.с. y будет

, (1.6)

и игроку II выгодно минимизировать v(y):

. (1.7)

Числа u*, v* называются соответственно нижней и верхней ценой игры в смешанных стратегиях.

Замечание. Строго говоря, следовало бы доказать, что все минимумы и максимумы в (1.4)-(1.7) существуют. Однако это очевидно, так как в силу (1.1), (1.2) множества X, Y компактны, а функции (1.3), (1.4) и (1.6) непрерывны.

Следующая лемма дает более простые, чем (1.4), (1.6) выражения величин u(x), v(y).

Лемма 1.1 [2] (о гарантированных выигрышах).

для всякой с.с. ;

для всякой с.с. .

Матричная игра называется разрешимой в с.с., если u* = v*, а стратегии u*, v*, для которых u(x*) = u* = v* = v(y*), называются оптимальными с.с. Пара (x*,y*) оптимальных с.с. образует ситуацию равновесия в с.с., а величина u* = v* – цена игры в с.с. – равна ожидаемому среднему выигрышу игрока I (и, соответственно, ожидаемому среднему проигрышу игрока II ).

Как и в случае чистых стратегий, несложно показать, что всегда u*≤v*. Однако, заметим, что в случае смешанных стратегий строгое неравенство u*<v* невозможно. Это вытекает из следующей основной теоремы матричных игр, доказанной Дж. фон Нейманом в 1928 г.

Теорема 1.2 [2] (о минимаксе). Для любой матричной игры имеет место равенство u* = v*. Другими словами, любая матричная игра разрешима в с.с.

Оптимальные с.с. игроков, а также цена игры в с.с. могут быть найдены как решения пары двойственных задач линейного программирования:

,

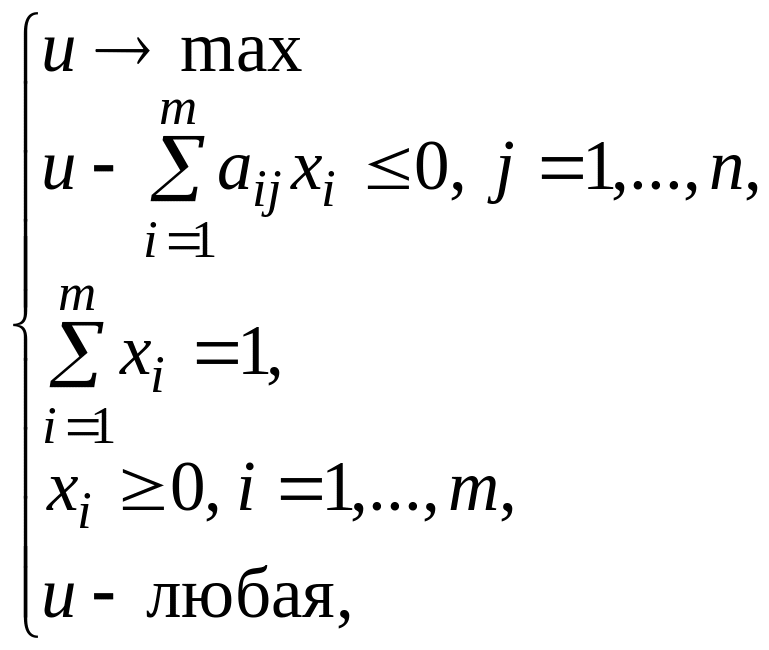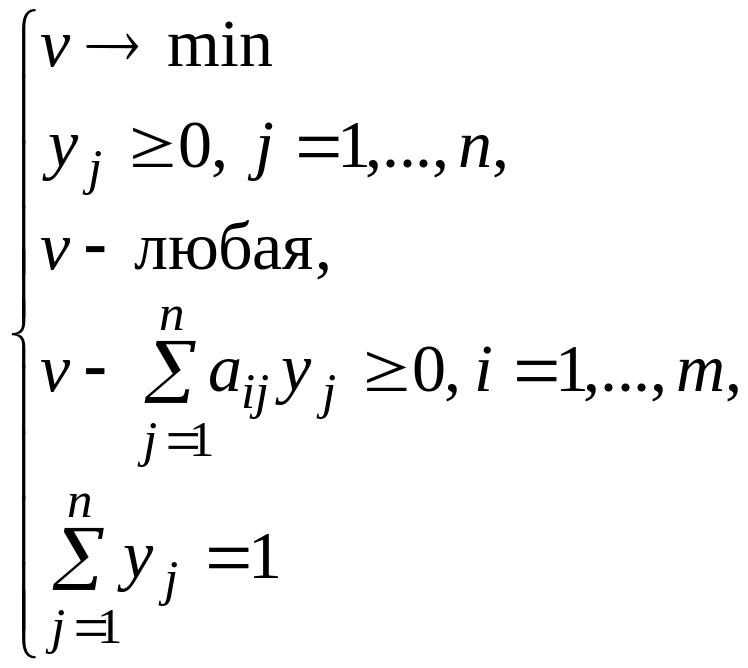
Здесь – элементы платежной матрицы A, переменные , – компоненты смешанных стратегий игроков I, II соответственно, u – гарантированный выигрыш игрока I, v – гарантированный проигрыш игрока II в с.с.

1.5 Пример полного решения матричной игры

Задача. Решить игру с платежной матрицей

.

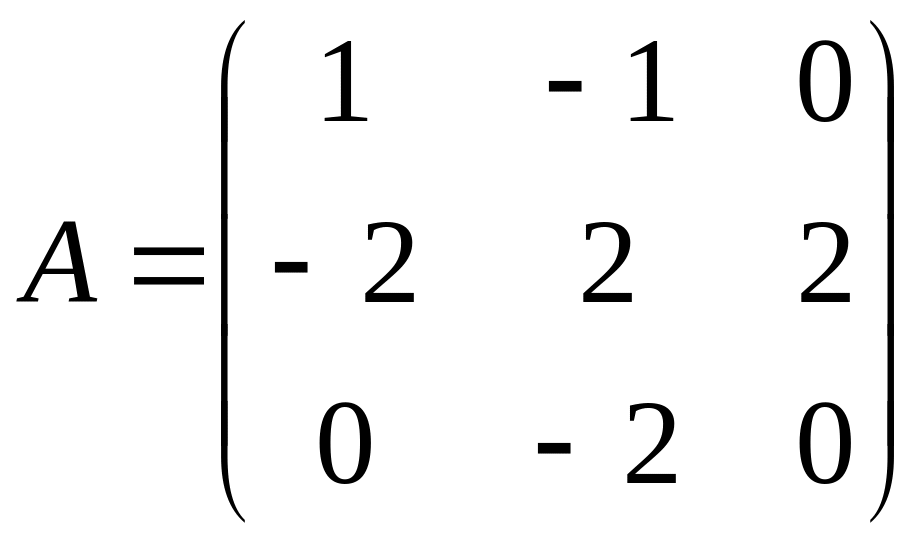Решение.

1. Выясним, имеет ли игра решение в ч.с. Для этого вычислим нижнюю и верхнюю цены игры в ч.с.:

; .

Получим, что a < b, следовательно, матрица A не имеет седловой точки, и игра не разрешима в ч.с.

2. Будем искать решение игры в с.с. Смешанная стратегия игрока I – это вероятностный вектор:

, где ; .

Аналогично смешанная стратегия игрока II – это вероятностный вектор:

, где ; .

3. Заметим, что каждый элемент строки 1 не меньше соответствующего элемента строки 3, то есть выигрыш игрока I при выборе им ч.с. 1 не меньше его выигрыша при выборе им ч.с. 3. Ясно, что разумный игрок I предпочтет стратегию 1 стратегии 3. В этом случае говорят, что ч.с. 1 игрока I доминирует над его ч.с. 3. Аналогично каждый элемент столбца 2 не больше соответствующего элемента столбца 3, и ч.с. 2 игрока II доминирует над его ч.с. 3. Легко понять, что в оптимальные с.с. доминируемые ч.с. войдут с нулевыми вероятностями , . Поэтому в дальнейшем мы можем рассматривать сокращенную матрицу игры, полученную из исходной вычеркиванием третьей строки и третьего столбца:

.

4. «Сдвиг» матрицы. Вместо матрицы рассмотрим матрицу

,

полученную из матрицы добавлением одного и того же числа ко всем ее элементам. Число это (в данном случае 2) выбирается так, чтобы все элементы матрицы стали неотрицательными. Несложно показать, что такой сдвиг платежной матрицы не приводит к изменению оптимальных смешанных стратегий игроков. Изменяется только значение цены игры, в данном случае оно увеличивается на 2.

Смысл такого сдвига в следующем. В игре с платежной матрицей выигрыш игрока I в любой ситуации неотрицателен, а значит, неотрицательны и все его гарантированные выигрыши, а также цена игры в с.с. Это дает нам право, составляя пару двойственных задач ЛП, считать переменные u, v неотрицательными.

5. Составляем пару двойственных задач для игры с платежной матрицей :

Прежде чем решать их, удобно сделать замену переменных , , i=1,2. Тогда задачи принимают вид

6. Приводим вторую задачу к канонической форме (вводя дополнительные переменные ), и решаем ее симплекс-методом [1]

Первая итерация

F	0	-1	-1	0	0
	1	3	1	1	0
	1	0	4	0	1

Вторая итерация

F	1/3	0	-2/3	1/3	0
	1/3	1	1/3	1/3	0
	1	0	4	0	1

Третья итерация

F	1/2	0	1	1/3	1/6
	1/4	1	0	1/3	-1/12
	1/4	0	1	0	1/4

Оптимальное решение , . Используя вторую теорему двойственности, находим оптимальное решение двойственной задачи: , . Возвращаясь к исходным переменным и вспоминая, что , , получаем оптимальные с.с. игроков: , . Цена игры в с.с. равна 0 (с учетом сдвига матрицы).

Комментарий. Оптимальные с.с. игроков диктуют им следующие действия при многократном повторении игры: игроку I следует выбирать свою первую ч.с. с вероятностью , а вторую – с вероятностью . Игроку II – выбирать как первую, так и вторую ч.с. с вероятностью . При этом ожидаемый средний выигрыш игрока I (и проигрыш игрока II) будет равен нулю – ничья.