
- •Учебное пособие по теоретической механике
- •Введение
- •Цели и задачи курсовой работы
- •Требования к уровню подготовки студентов
- •Календарный план выполнения курсовой работы
- •Пояснения по тексту заданий курсовой работы
- •Требования к оформлению курсовой работы
- •Структура пояснительной записки
- •Защита курсовой работы
- •Часть 1. Статика Задание с1. Определение реакций опор балки.
- •Пример выполнения задания с1.
- •Задание с2. Определение реакций опор угольника.
- •Пример выполнения задания с2.
- •Задание с3. Определение центра тяжести фигуры
- •Пример выполнения задания с3.
- •Кинематика Задание к1 Определение кинематических характеристик движения материальной точки
- •Пример решения задания к1
- •Задание к2
- •Пример решения задания к2
- •Решение
- •Форма задания на курсовую работу
- •Титульный лист пояснительной записки курсовой работы
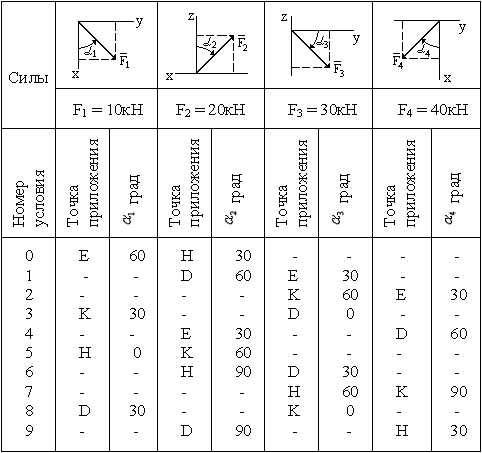
Задание с2. Определение реакций опор угольника.
Две однородные прямоугольные пластины,
приваренные под прямым углом друг к
другу, образуют угольник, который
закреплен с помощью различного типа
связей в точках А, В, О (на рис. С2.8 и С2.9
еще и в точке L). Размеры пластин в
направлениях, параллельных координатным
осям х, у, z равны
соответственно или
![]() ,
,
![]() и
(рис.С2.0 – С2.4), или
,
и
и
(рис.С2.0 – С2.4), или
,
и
![]() (рис.
С2.5 – С2.9). Вес одной из пластин равен G1
= 5 кН, вес второй – G2 =
2 кН. Каждая из пластин расположена
параллельно одной из координатных
плоскостей (плоскость ху горизонтальная).
(рис.
С2.5 – С2.9). Вес одной из пластин равен G1
= 5 кН, вес второй – G2 =
2 кН. Каждая из пластин расположена
параллельно одной из координатных
плоскостей (плоскость ху горизонтальная).
На пластины действуют: пара сил с моментом
М = 10 кНм, лежащая в
плоскости одной из пластин, и две силы.
Величины этих сил, их направления и
точки приложения указаны в таблице С2
при этом силы
![]() и
и
![]() лежат в плоскостях, параллельных
плоскости ху, сила
лежат в плоскостях, параллельных
плоскости ху, сила
![]() - в плоскости параллельной хz,
и сила
- в плоскости параллельной хz,
и сила
![]() в плоскости, параллельной уz.
Точки приложения сил (D,
E, H, K)
находятся в углах или в серединах сторон
пластин.
в плоскости, параллельной уz.
Точки приложения сил (D,
E, H, K)
находятся в углах или в серединах сторон
пластин.
Определить реакции связей. При расчетах принять = 0,5 м. Толщиной пластин пренебречь.
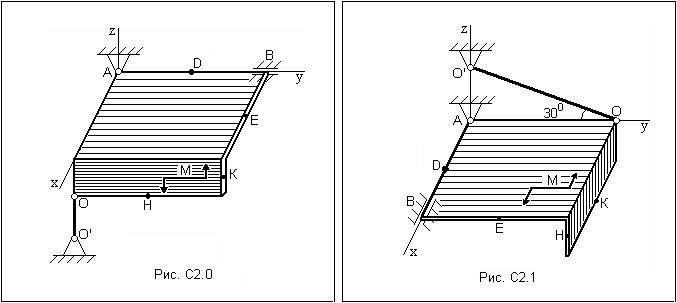
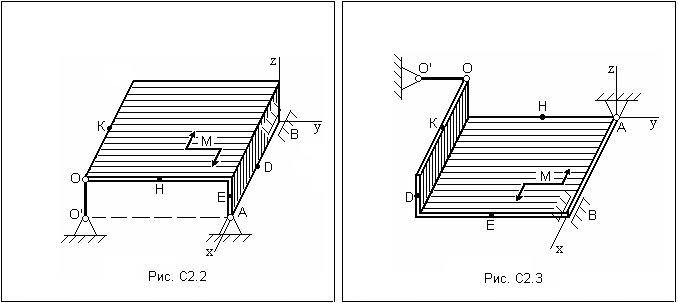
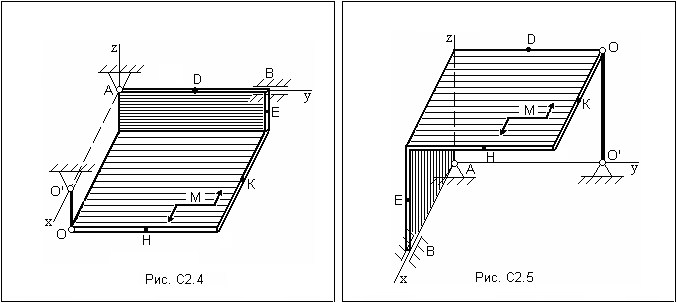
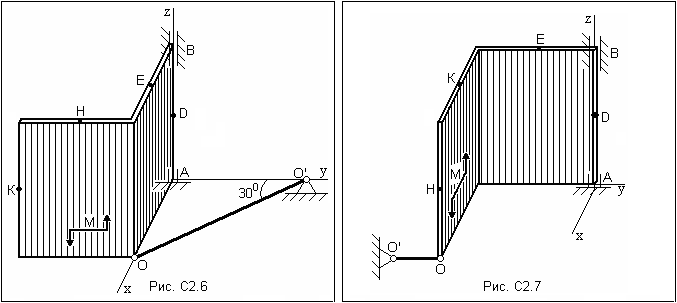
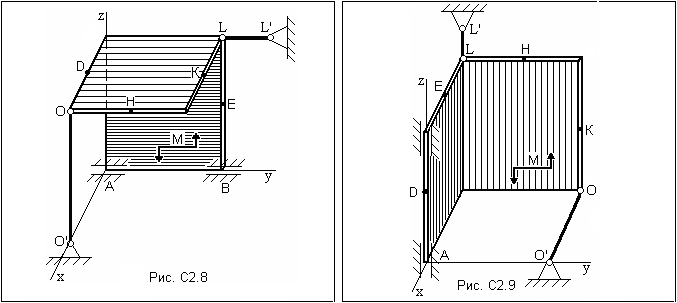
Таблица С2
Указания. Для определения реакций
связей следует использовать уравнения
равновесия тела, находящегося под
действием пространственной произвольной
системы сил. При решении учесть, что
реакция сферического шарнира (или
подпятника) раскладывается на три
составляющие, реакция цилиндрического
шарнира (подшипника) – на две составляющие,
лежащие в плоскости, перпендикулярной
оси шарнира, а реакция стержня, шарнирно
закрепленного по обоим концам, направлена
вдоль стержня. При вычислении моментов
каждой из сил
![]() удобно разложить эту силу на составляющие,
например,
удобно разложить эту силу на составляющие,
например,
![]() и
(если
необходимо, то и
и
(если
необходимо, то и
![]() )
параллельные координатным осям, и
воспользоваться теоремой Вариньона;
тогда Мo(
)
= Mo(
)
+ Mo(
)
параллельные координатным осям, и
воспользоваться теоремой Вариньона;
тогда Мo(
)
= Mo(
)
+ Mo(![]() )
и т.д.
)
и т.д.
Пример выполнения задания с2.
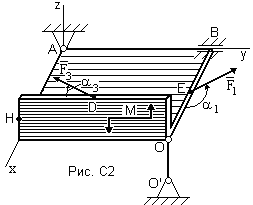
Две однородные прямоугольные пластины, сваренные под прямым углом друг к другу, закреплены с помощью связей в точках А, В, О. Размеры пластин в направлениях, параллельных координатным осям х, у, z равны соответственно или , и . Вес большей пластины равен G1 = 5 кН, вес меньшей - G2 = 2 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (оси ху образуют горизонтальную плоскость).
На пластины действуют пара сил с
моментом М = 5 кНм
и две силы
и
при этом сила
лежит в плоскости хАу, сила
![]() лежит в плоскости, параллельной плоскости
уАz. Точки приложения
сил находятся в серединах сторон пластин.
лежит в плоскости, параллельной плоскости
уАz. Точки приложения
сил находятся в серединах сторон пластин.
Определить реакции связей в точках А, В, О. При расчетах принять = 0,5 м, F1= 20 кН, α1 = 1350, F3 = 30 кН, α3 = 300. Толщиной пластин пренебречь.
Решение
Для нахождения реакций связей покажем заданные по условию задачи активные воздействия: силы F1 и F3, момент пары сил M, силы тяжести каждой из пластин. Объектом равновесия является твердое тело – угольник, образованный двумя жестко соединенными пластинами. На это тело связи наложены в точках А, В, О. Применим принцип освобождаемости от связей и покажем в этих точках реакции:
- в точке А связью является сферический шарнир, его реакции ХА, УА, ZА,
- в точке В связью является цилиндрический шарнир, его реакции ХВ, ZВ,
- в точке О связью является тонкий невесомый стержень, шарнирно опертый по обоим концам, реакция RО.
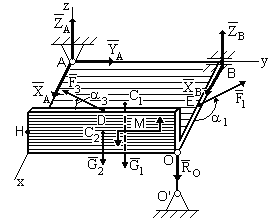
Величины сил тяжести пластин G1 и G2 приложены в центрах тяжести плит С1 и С2, которые находятся на пересечении диагоналей.
На рисунке получилась произвольная пространственная система сил; запишем условия и составим уравнения равновесия для этой системы сил. При составлении уравнений моментов сил целесообразно использовать теорему Вариньона, для чего силы и раскладываются на составляющие, параллельные осям координат
![]() и
и
![]() ,
,
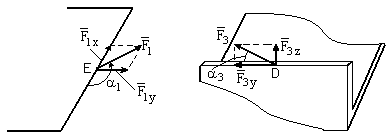
где
![]()
![]() ,
,
![]()
![]() .
.
Уравнения равновесия имеют вид:
∑Fix
= 0 XА + ХВ –
F1cos![]() = 0;
(1)
= 0;
(1)
∑Fiy
= 0 YA
+ F1sin
– F3 cos![]() = 0; (2)
= 0; (2)
∑Fiz
= 0
![]() ;
(3)
;
(3)
∑Mхi
= 0
![]() ;
(4)
;
(4)
∑Mуi
= 0
![]() ;
(5)
;
(5)
∑Mzi
= 0
![]() .
(6)
.
(6)
Из уравнения (6) найдем реакцию ХВ
![]() (
(![]() ,
,
из уравнения (5) найдем величину реакции
в точке О
![]()
![]() ,
,
из уравнения (4) найдем
![]()
![]() .
.
После нахождения
![]()
![]() ,
,
![]() ,
не представляет труда из уравнений (1),
(2), (3) найти выражения для остальных
неизвестных реакций
,
не представляет труда из уравнений (1),
(2), (3) найти выражения для остальных
неизвестных реакций
XА = – ХВ + F1cos ,
YA
= – F1sin
+ F3 cos![]() ,
,
![]() .
.
Подставляя в полученные выражения значения параметров можно вычислить числовые значения реакций связей.
