
- •1 Курс, 2 семестр
- •Практические занятия
- •Перечень типовых задач по теме «Скалярное, векторное и смешанное произведения векторов»
- •Перечень типовых задач по теме «Плоскости в пространстве»
- •1. Аффинные задачи
- •2. Метрические задачи
- •Перечень типовых задач по теме «Прямые в пространстве»
- •1. Аффинные задачи
- •2. Метрические задачи
- •Перечень типовых задач по теме «Прямые и плоскости в пространстве»
- •1. Аффинные задачи
- •2. Метрические задачи
- •Перечень типовых задач по теме «Эллипс»
- •Перечень типовых задач по теме «Гипербола»
- •Перечень типовых задач по теме «Парабола»
- •Перечень типовых задач по теме «Понятие о классификации линий второго порядка»
- •2 Курс, 3 семестр
- •III семестр
- •Список литературы для подготовки к практическим занятиям
- •Перечень типовых задач по теме «Поверхности вращения. Цилиндрические поверхности. Конические поверхности»
- •Перечень типовых задач по теме «Эллипсоиды. Гиперболоиды. Параболоиды. Прямолинейные образующие поверхностей второго порядка»
- •Перечень типовых задач по теме «Движения плоскости. Виды, свойства и аналитическое выражение движений»
- •Перечень типовых задач по теме «Построение сечений многогранников»
- •2 Курс, 4 семестр
- •IV семестр
- •Перечень типовых задач по теме «Расширенное евклидово пространство»
- •Перечень типовых задач по теме «Проективные координаты. Уравнение проективной прямой»
- •Перечень типовых задач по теме «Теорема Дезарга. Приложение к решению задач»
- •Перечень типовых задач по теме «Сложное отношение четырёх точек прямой и четырёх прямых пучка. Гомология»
- •Перечень типовых задач по теме «Гармонизм. Полный четырёхвершинник. Приложение свойств полного четырёхвершинника к решению задач»
- •Перечень типовых задач по теме «Полюс и поляра. Поляритет и его свойства»
- •Перечень типовых задач по теме «Теоремы Паскаля и Брианшона. Приложение к решению задач»
- •Перечень типовых задач по теме «Система аксиом Гильберта»
- •Перечень типовых задач по теме «Решение задач на плоскости Лобачевского»
- •Перечень типовых задач по теме «Понятие об интерпретации системы аксиом. Требования, предъявляемые к системе аксиом»
- •Перечень типовых задач по теме «Система аксиом Вейля трёхмерного евклидова пространства»
Список литературы для подготовки к практическим занятиям
1. Линейная алгебра и аналитическая геометрия: Учебное пособие для студентов высших учебных заведений по специальности «Информатика». − 2-е изд., перераб. / Составители: Л.Т. Крежевских, И.Л. Мирошниченко. − Глазов: Глазов. гос. пед. ин-т, 2007. − 96 с.
2. Линейная алгебра и аналитическая геометрия: Пособие к практическим занятиям для студентов факультета социальных и информационных технологий. / Составители: Л.Т. Крежевских, И.Л. Мирошниченко. − Глазов: Изд. центр ГГПИ, 2005. − 96 с.
3. Методическая разработка к практическим занятиям по геометрии (электронный вариант) / Составитель: Л.Т. Крежевских. − Глазов: 2007.
4. Практические занятия по проективной геометрии и методам изображений (Методические рекомендации в помощь студентам). − Глазов, 1993. − 60 с.
Перечень типовых задач по теме «Поверхности вращения. Цилиндрические поверхности. Конические поверхности»
Предварительно необходимо:
изучить теоретические сведения по указанной теме;
ответить на контрольные вопросы I.17 − I.22 занятия 16 из методического пособия [1];
познакомиться с решениями следующих задач из методического пособия [3]: тема 1, задачи 1.1, 1.2; тема 2, задачи 1.1 − 1.3; тема 3, задачи 1.1 − 1.3.
Задачи для решения на практическом занятии: [3], тема 1, №№ 2.1− 2.7; тема 2, №№ 2.1 − 2.4; тема 3, №№ 2.1 − 2.5.
Задачи для самостоятельного решения: [3], тема 1, №№ 3.1 − 3.9; тема 2, №№ 3.1 − 3.4; тема 3, №№ 3.1 − 3.5.
Перечень типовых задач по теме «Эллипсоиды. Гиперболоиды. Параболоиды. Прямолинейные образующие поверхностей второго порядка»
Предварительно необходимо:
изучить теоретические сведения по указанной теме;
ответить на контрольные вопросы I.1 − I.16 занятия 16 из методического пособия [1];
познакомиться с решениями следующих задач из методического пособия [3]: тема 4, задачи 1.1 − 1.3; тема 5, задачи 1.1, 1.2.
Задачи для решения на практическом занятии: [3], тема 4, №№ 2.1− 2.6; тема 5, №№ 2.1 − 2.4.
Дополнительно:
1. Привести уравнение к каноническому виду и определить вид поверхности:
а) 3х + 10у2 = 0; д) 2у2 – 17 = 0;
б) 5х2 − 12у2 = 0; е) 9х2 + у2 − z2 = 0;
в) 4х2 − 2у2 + 3z2 = 0; ж) х2 − у2 + z2 = 0;
г) 6у2 − 25z2 + 150 = 0; з) 100х2 − 16z2 − 1 = 0.
2. Привести уравнение к каноническому виду и определить вид поверхности:
а)
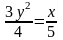 ; г)
3х2
+ 2у2
− z2
+ 1 = 0;
; г)
3х2
+ 2у2
− z2
+ 1 = 0;
б)
х2
−
 у2
− 1 = 0; д) 25х2
− 4у2
− 100z2
− 25 = 0;
у2
− 1 = 0; д) 25х2
− 4у2
− 100z2
− 25 = 0;
в) х2 − 3у2 − 7z2 +1 = 0; е) 9х2 − у2 − 9z2 + 9 = 0.
Задачи для самостоятельного решения: [1], занятие 16, №№ III.1 − III.4, IV.1 − IV.3, V.2, V.3; [3], тема 4, №№ 3.1 − 3.7; тема 5, №№ 3.1 − 3.6.
Перечень типовых задач по теме «Движения плоскости. Виды, свойства и аналитическое выражение движений»
Предварительно необходимо:
изучить теоретические сведения по указанной теме;
познакомиться с решениями следующих задач из методического пособия [3]: тема 6, задачи 1.1 − 1.3; тема 7, задачи 1.1, 1.2.
Задачи для решения на практическом занятии: [3], тема 6, №№ 2.1− 2.6; тема 7, №№ 2.1 − 2.4, 2.6.
Задачи для самостоятельного решения: [3], тема 6, №№ 3.1 − 3.5; тема 7, №№ 3.1 − 3.4.
Перечень типовых задач по теме
«Подобия плоскости. Гомотетия.
Их свойства и аналитическое выражение»
Предварительно необходимо:
изучить теоретические сведения по указанной теме;
познакомиться с решениями следующих задач из методического пособия [3]: тема 9, задачи 1.1 − 1.3.
Задачи для решения на практическом занятии: [3], тема 9, №№ 2.1− 2.3, 2.5.
Задачи для самостоятельного решения: [3], тема 9, №№ 3.1 − 3.4.
Перечень типовых задач по теме
«Аффинные преобразования плоскости,
их свойства и аналитическое выражение.
Перспективно-аффинные преобразования плоскости»
Предварительно необходимо:
изучить теоретические сведения по указанной теме;
познакомиться с решениями следующих задач из методического пособия [3]: тема 10, задачи 1.1 − 1.3.
Задачи для решения на практическом занятии: [3], тема 10, №№ 2.1− 2.7.
Задачи для самостоятельного решения: [3], тема 10, №№ 3.1 − 3.3.
Перечень типовых задач по теме
«Изображение плоских и пространственных фигур
в параллельной проекции»
Предварительно необходимо:
изучить теоретические сведения по темам: «Параллельное проектирование и его свойства», «Изображение плоских фигур в параллельной проекции», «Изображение многогранников, цилиндра, конуса и шара в параллельной проекции»;
ответить на контрольные вопросы и выполнить следующие задания: [4], занятие 6, №№ II.1 − II.12; занятие 8, №№ II.1 − II.6.
Задачи
Построить изображение: а) прямоугольника с отношением сторон 2:3; б) равнобокой трапеции с отношением оснований 2:5.
Построить изображение правильного треугольника, вписанного в окружность.
Построить изображение: а) правильного шестиугольника, вписанного в окружность; б) правильного восьмиугольника, вписанного в окружность.
Построить изображение правильного шестиугольника, используя свойства правильного шестиугольника.
Дано изображение A, B, D трёх вершин
 ,
,
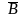 и
и
 правильного шестиугольника
правильного шестиугольника
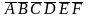 .
Достроить его изображение.
.
Достроить его изображение.Дано изображение С, D и Е трёх соседних вершин правильного шестиугольника. Достроить изображение остальных его вершин.
Построить изображение произвольного семиугольника.
Построить изображение окружности и её сегмента с углом: а) 30º; б) 60º; в) 45º; г) 75º; д) 105º.
Построить изображение окружности и её сектора с углом: а) 30º; б) 60º; в) 45º; г) 75º; д) 105º.
Дано изображение произвольного треугольника и двух его высот. Построить изображение центра описанной около этого треугольника окружности.
Дано изображение произвольного треугольника, вписанного в окружность. Построить изображение его высот.
Построить изображение: а) треугольной призмы, вписанной в цилиндр; б) треугольной призмы, описанной около цилиндра.
Построить изображение: а) пятиугольной призмы, вписанной в цилиндр; б) пятиугольной призмы, описанной около цилиндра.
Построить изображение: а) треугольной пирамиды, вписанной в конус; б) треугольной пирамиды, описанной около конуса.
Построить изображение: а) правильной четырёхугольной пирамиды, вписанной в конус; б) правильной четырёхугольной пирамиды, описанной около конуса.
Построить изображение треугольной пирамиды, вписанной в шар.
