Перечень типовых задач по теме «Гипербола»
Предварительно необходимо:
● изучить § 29 по электронным текстам и по конспектам лекций по аналитической геометрии, выучить все определения, формулировки свойств, формулы и уравнения;
● ответить на контрольные вопросы и задания I.7 – I.13 занятия 15 (см. методическое пособие «Линейная алгебра и аналитическая геометрия»);
● ознакомиться с решением задачи II.1 занятия 15.
Задачи
(решаются в прямоугольной декартовой системе координат О )
43. Дано каноническое уравнение гиперболы . Найти действительную и мнимую полуоси, фокальное расстояние, координаты вершин, фокусов, эксцентриситет, уравнения асимптот и директрис, уравнение сопряженной с ней гиперболы и выполнить чертеж гиперболы, ее фокусов, асимптот и директрис, если:
а)
;
б)
;
в)
.
44. Дано уравнение гиперболы . Привести его к каноническому виду и найти действительную и мнимую полуоси, фокальное расстояние, координаты вершин, фокусов, эксцентриситет, уравнения асимптот и директрис и выполнить чертеж гиперболы, ее фокусов, асимптот и директрис, если:
а)
;
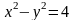б)
;
в)
.
45. Найти каноническое уравнение гиперболы и выполнить чертеж гиперболы, ее фокусов, асимптот и директрис, если известно, что:
а)
мнимая полуось равна 4, эксцентриситет
равен
,
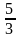Оу
– мнимая ось гиперболы;
б)
фокальное расстояние равно
,
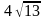уравнения асимптот
,
,
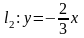Оу – мнимая
ось гиперболы;
в)
гипербола проходит через точку
,
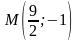уравнения асимптот
,
,
Оу – мнимая
ось гиперболы;
г)
гипербола проходит через точку
,
эксцентриситет равен
,
Оу – мнимая
ось гиперболы;
д)
мнимая полуось равна
,
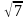уравнения директрис
,
.
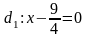46. Падающая на крышу тень имеет форму гиперболы, расстояние между фокусами которой равно 20. Найти каноническое уравнение этой гиперболы, если ее эксцентриситет равен .
Перечень типовых задач по теме «Парабола»
Предварительно необходимо:
● изучить § 30 по электронным текстам и по конспектам лекций по аналитической геометрии, выучить все определения, формулировки свойств, формулы и уравнения;
● ответить на контрольные вопросы и задания I.14 – I.19 занятия 15 (см. методическое пособие «Линейная алгебра и аналитическая геометрия»);
● ознакомиться с решением задачи II.3 занятия 15.
Задачи
(решаются в прямоугольной декартовой системе координат О )
47. Дано каноническое уравнение параболы . Определить фокальный параметр, координаты фокуса, уравнение директрисы, эксцентриситет параболы и выполнить чертеж параболы, ее фокуса и директрисы:
а)
|
г)
|
б)
|
д)
|
в)
|
|
;
;
;
.
;48. Дано уравнение параболы . Привести его к каноническому виду и определить ось и фокальный параметр параболы:
а)
|
г)
|
б)
|
д)
|
в)
|
|
;
;
;
.
;49. Найти каноническое уравнение параболы, вершина которой находится в начале координат, и выполнить чертеж параболы, ее фокуса и директрисы, если:
а)
фокус имеет координаты
;
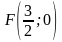б)
уравнение директрисы
;
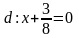в)
парабола проходит через точку
,
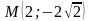Ох
– ось параболы.
50. Камень, брошенный под острым углом к горизонту, описал дугу параболы и упал на расстоянии 16 м от начального положения. Определить фокальный параметр параболической траектории, зная, что наибольшая высота, достигнутая камнем, равна 12 м.
51. Мостовая арка имеет форму параболы. Определить фокальный параметр этой параболы, зная, что пролет арки равен 24 м, а высота – 6 м.
52. Зеркало автомобильной фары имеет в разрезе форму параболы. Диаметр зеркала 20 см, глубина – 10 см. Найти фокальный параметр зеркала.
53. Струя воды,
выбрасываемая фонтаном, имеет форму
параболы, фокальный параметр которой
р
= 0,1 м. определить высоту
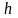струи, если известно, что она падает в
бассейн на расстоянии 2 м от места выхода.
54. Поперечное сечение крыши вагона имеет форму параболы. Ширина крыши 3,6 м. Определить высоту крыши, если на расстоянии 1,44 м от края высота крыши 0,48 м.
55. Стальной трос подвешен за два конца. Точки крепления расположены на одинаковой высоте. Расстояние между ними равно 20 м. Величина его прогиба на расстоянии 2 м от точки крепления, считая по горизонтали, равна 14,4 см. Определить величину прогиба этого троса в середине между точками крепления, приближенно считая, что трос имеет форму дуги параболы.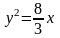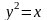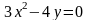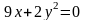