
- •1 Курс, 2 семестр
- •Практические занятия
- •Перечень типовых задач по теме «Скалярное, векторное и смешанное произведения векторов»
- •Перечень типовых задач по теме «Плоскости в пространстве»
- •1. Аффинные задачи
- •2. Метрические задачи
- •Перечень типовых задач по теме «Прямые в пространстве»
- •1. Аффинные задачи
- •2. Метрические задачи
- •Перечень типовых задач по теме «Прямые и плоскости в пространстве»
- •1. Аффинные задачи
- •2. Метрические задачи
- •Перечень типовых задач по теме «Эллипс»
- •Перечень типовых задач по теме «Гипербола»
- •Перечень типовых задач по теме «Парабола»
- •Перечень типовых задач по теме «Понятие о классификации линий второго порядка»
- •2 Курс, 3 семестр
- •III семестр
- •Список литературы для подготовки к практическим занятиям
- •Перечень типовых задач по теме «Поверхности вращения. Цилиндрические поверхности. Конические поверхности»
- •Перечень типовых задач по теме «Эллипсоиды. Гиперболоиды. Параболоиды. Прямолинейные образующие поверхностей второго порядка»
- •Перечень типовых задач по теме «Движения плоскости. Виды, свойства и аналитическое выражение движений»
- •Перечень типовых задач по теме «Построение сечений многогранников»
- •2 Курс, 4 семестр
- •IV семестр
- •Перечень типовых задач по теме «Расширенное евклидово пространство»
- •Перечень типовых задач по теме «Проективные координаты. Уравнение проективной прямой»
- •Перечень типовых задач по теме «Теорема Дезарга. Приложение к решению задач»
- •Перечень типовых задач по теме «Сложное отношение четырёх точек прямой и четырёх прямых пучка. Гомология»
- •Перечень типовых задач по теме «Гармонизм. Полный четырёхвершинник. Приложение свойств полного четырёхвершинника к решению задач»
- •Перечень типовых задач по теме «Полюс и поляра. Поляритет и его свойства»
- •Перечень типовых задач по теме «Теоремы Паскаля и Брианшона. Приложение к решению задач»
- •Перечень типовых задач по теме «Система аксиом Гильберта»
- •Перечень типовых задач по теме «Решение задач на плоскости Лобачевского»
- •Перечень типовых задач по теме «Понятие об интерпретации системы аксиом. Требования, предъявляемые к системе аксиом»
- •Перечень типовых задач по теме «Система аксиом Вейля трёхмерного евклидова пространства»
2. Метрические задачи
(решаются в прямоугольной декартовой системе координат О )
19. Найти канонические
уравнения прямой
,
проходящей через точку
 и перпендикулярной прямым
и перпендикулярной прямым

 и
и
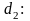
 .
.
20. Найти величину угла между прямыми:
а)
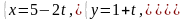 и
и
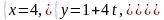
б)
 и
и

21. Выяснить, будут
ли прямые
 и
и
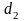 взаимно перпендикулярными:
взаимно перпендикулярными:
а)
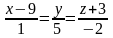 ;
;

б)
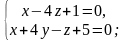
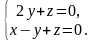
Перечень типовых задач по теме «Прямые и плоскости в пространстве»
Предварительно необходимо:
● изучить §§ 26 (п. 2), 27 (п. 3, 4) по электронным текстам и по конспектам лекций по аналитической геометрии, а также знать материал §§ 20 – 22, 24 (п. 1), 25;
● ответить на контрольные вопросы и выполнить в тетрадях для практических занятий все контрольные задания из пункта I занятия 14 (см. методическое пособие «Линейная алгебра и аналитическая геометрия»);
● ознакомиться с решениями всех задач из пункта II занятия 14.
1. Аффинные задачи
(решаются в аффинной системе координат О )
22. Найти уравнение
плоскости
,
проходящей через точку
и параллельной прямым
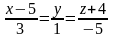 и
и

23. Найти уравнение
плоскости
,
содержащей прямую
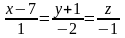 и параллельной прямой
и параллельной прямой
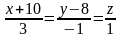 .
.
24. Найти уравнение
плоскости
,
содержащей прямые
 и
и
 .
.
25. Найти уравнение
плоскости
,
содержащей прямые
 и
и
 .
.
26. Найти уравнение
плоскости
,
проходящей через точку
и содержащей прямую

27. Найти уравнение
плоскости
,
содержащей прямую
 и параллельной прямой
и параллельной прямой
 .
.
28. Найти уравнение
плоскости
,
проходящей через точки
 и
и
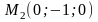 и параллельной прямой
и параллельной прямой
 .
.
29. Выяснить взаимное
расположение прямой
 и плоскости
:
и плоскости
:
а)
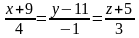 ;
;
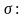
 ;
;
б)

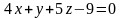 ;
;
в)
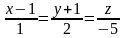 ;
;
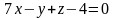 .
.
2. Метрические задачи
(решаются в прямоугольной декартовой системе координат О )
30. Найти уравнение
плоскости
,
проходящей через точку
и перпендикулярной прямой
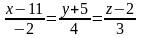 .
.
31. Найти уравнение
прямой
,
проходящей через точку
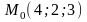 и перпендикулярной плоскости
и перпендикулярной плоскости
 .
.
32. Найти уравнение
плоскости
,
проходящей через точку
 ,
параллельной прямой
,
параллельной прямой
 и перпендикулярной плоскости
и перпендикулярной плоскости
 .
.
33. Найти уравнение плоскости , содержащей прямую и перпендикулярной плоскости .
34. Найти синус угла
между прямой d:
 и плоскостью σ:
и плоскостью σ:
 .
.
35. Выяснить, будут ли прямая и плоскость взаимно перпендикулярными:
а)
 б)
б)

 ;
;
 .
.
Перечень типовых задач по теме «Эллипс»
Предварительно необходимо:
● изучить § 28 по электронным текстам и по конспектам лекций по аналитической геометрии, выучить все определения, формулировки свойств, формулы и уравнения;
● ответить на контрольные вопросы и задания I.1 – I.6 занятия 15 (см. методическое пособие «Линейная алгебра и аналитическая геометрия»);
● ознакомиться с решением задачи II.2 занятия 15.
Задачи
(решаются в прямоугольной декартовой системе координат О )
36. Дано каноническое
уравнение эллипса
.
Найти большую и малую полуоси, фокальное
расстояние, координаты вершин, фокусов,
эксцентриситет, уравнения директрис,
фокальные радиусы точки
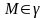 и выполнить чертеж эллипса, его фокусов
и директрис, если:
и выполнить чертеж эллипса, его фокусов
и директрис, если:
а)

 ,
,
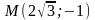 ;
;
б)
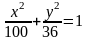 ,
,
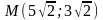 ;
;
в)
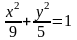 ,
,
 .
.
37. Найти каноническое уравнение эллипса и выполнить чертеж эллипса, его фокусов и директрис, если известно, что:
а) фокальное расстояние равно 6, а большая полуось равна 5;
б)
малая полуось равна 3, уравнения директрис
 ,
,
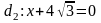 ;
;
в)
малая полуось равна 4, эксцентриситет
равен
 ;
;
г)
эллипс проходит через точку
 ,
эксцентриситет равен
,
эксцентриситет равен
 .
.
38. Меридиан Земного шара имеет форму эллипса, отношение осей которого равно 299 : 300. Определить эксцентриситет земного меридиана.
39. Орбита Земли
относительно Солнца – эллипс с полуосью
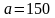 млн. км и эксцентриситетом
млн. км и эксцентриситетом
 .
Найти разность максимального и
минимального расстояний от Земли до
Солнца, если Солнце находится в одном
из фокусов орбиты Земли.
.
Найти разность максимального и
минимального расстояний от Земли до
Солнца, если Солнце находится в одном
из фокусов орбиты Земли.
40.Масимальное удаление ракеты от поверхности Земли – 197 млн. км, минимальное – 147 млн. км. Составить уравнение траектории движения ракеты, если она движется вокруг Земли по эллипсу, в одном из фокусов которого находится Земля.
41. Орбита космической ракеты представляет собой эллипс, эксцентриситет которого равен 0,14. Найти отношение полуосей этого эллипса.
42. Земля движется по эллипсу, в одном из фокусов которого находится Солнце. Наименьшее расстояние от Земли до Солнца равно приблизительно 147500000 км, а наибольшее – 152500000 км. Найти большую полуось и эксцентриситет орбиты Земли.
