Перечень типовых задач по теме «Понятие об интерпретации системы аксиом. Требования, предъявляемые к системе аксиом»
Предварительно необходимо изучить теоретические сведения по темам «Понятие о математической структуре», «Понятие об интерпретации системы аксиом. Содержательная и внутренняя непротиворечивость системы аксиом. Изоморфизм интерпретаций», «Независимость и полнота системы аксиом».
Доказать, что I группа аксиом Гильберта содержательно непротиворечива.
Доказать, что аксиома I.1 Гильберта не зависит от остальных аксиом первой группы.
Сформулированы следующие аксиомы инцидентности:
А1. Любым двум различным точкам можно отнести прямую, им инцидентную.
А2. Любым двум различным точкам можно отнести не более одной прямой, им инцидентной.
А3. На каждой прямой существует по крайней мере две точки, ей инцидентные.
А4. Существует тройка точек, не инцидентных одной прямой.
Доказать независимость каждой из аксиом А1−А4 от остальных.
Дана аксиоматика:
А1. Существуют три точки, не лежащие на одной прямой.
А2. Для любых двух различных точек существует единственная прямая, проходящая через эти точки.
А3. Если точка М
не принадлежит прямой а,
то существует единственная прямая l
такая, что
и
.
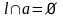Доказать содержательную непротиворечивость этой системы аксиом.
Точкой назовём каждую из следующих троек чисел (0; 0; 0), (1; 0; 0), (0; 1; 0) и (0; 0; 1). Три числа − это координаты точки. Прямая − это каждая из следующих систем:
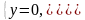
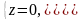
Плоскость
− это каждое из четырёх уравнений: х
= 0, у
= 0, z
= 0 и
.
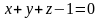Точка А
принадлежит прямой а
(плоскости α)
тогда и только тогда, когда её координаты
удовлетворяют системе уравнений а
(уравнению α).
Доказать, что выполняются все аксиомы
первой группы Гильберта.
Перечень типовых задач по теме «Система аксиом Вейля трёхмерного евклидова пространства»
Предварительно необходимо изучить теоретические сведения по теме «Система аксиом Вейля трёхмерного евклидова пространства и основные следствия из неё».
Сформулировать аксиоматику Вейля n-мерного евклидова пространства и доказать её непротиворечивость.
Доказать, что в аксиоматике Вейля трёхмерного евклидова пространства аксиомы третьей группы не зависят от остальных аксиом.
Назовём вектором любую квадратную матрицу
,
где
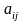− действительные числа, i,
j
= 1, 2; суммой векторов − сумму матриц;
произведением числа λ
на вектор − произведение λ
на матрицу. Доказать, что аксиома III.2
Вейля не зависит от остальных аксиом
I
– III
групп.Назовём суммой векторов произведение матриц. Остальные соглашения − как в задаче 39. Проверить выполнимость аксиом I и II групп Вейля.
Назовём скалярным произведением векторов
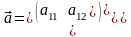и
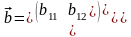число
.
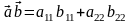Остальные соглашения − как в задаче
39. Проверить выполнимость аксиом IV
группы Вейля.Доказать с помощью аксиом Вейля I и II групп, что если
,
то
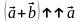и
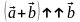.Доказать с помощью аксиом Вейля, что в любом треугольнике АВС имеет место соотношение: а) АС < АВ + ВС; б) АС > АВ − ВС.
В треугольнике АВС проведена высота CD. Доказать с помощью аксиом Вейля, что если: 1) CD >
,
то
<
90º;
2) CD = , то = 90º;
3) CD < , то > 90º.
Доказать с помощью аксиом Вейля, что если в треугольнике АВС медиана СС1 перпендикулярна к стороне АВ, то он равнобедренный, т.е СА = СВ.
С помощью аксиом Вейля доказать, что диагонали квадрата взаимно перпендикулярны и равны.
В треугольнике АВС проведена медиана CD. Доказать с помощью аксиом Вейля, что если ВС > AC, то
−
тупой.В треугольнике АВС проведена медиана CD. Доказать с помощью аксиом Вейля, что 1) если СD >
AB,
то
−
острый;
2) если СD = AB, то − прямой;
3) если СD < AB, то − тупой.
Доказать с помощью аксиом Вейля теорему о трёх перпендикулярах: прямая, проведённая на плоскости через основание наклонной и перпендикулярная к её проекции, перпендикулярна и к самой наклонной и наоборот.
Доказать с помощью аксиом Вейля, что в произвольном тетраэдре отрезки, соединяющие середины противоположных рёбер, пересекаются в одной точке и делятся в ней пополам.
Доказать с помощью аксиом Вейля, что в правильном тетраэдре отрезки, соединяющие середины противоположных сторон, попарно перпендикулярны и равны.