3. 2. 3. Добавление элемента
Наиболее простой способ добавить элемент в список - это вставить его в самое начало так, чтобы он стал его новой головой. Если Х - это новый элемент, а список, в который Х добавляется - L, тогда результирующий список - это просто
[X | L]
Таким образом, для того, чтобы добавить новый элемент в начало списка, не надо использовать никакой процедуры. Тем не менее, если мы хотим определить такую процедуру в явном виде, то ее можно представить в форме такого факта:
добавить( X, L, [X | L] ).
3. 2. 4. Удаление элемента
Удаление элемента Х из списка L можно запрограммировать в виде отношения
удалить( X, L, L1)
где L1 совпадает со списком L, у которого удален элемент X. Отношение удалить можно определить аналогично отношению принадлежности. Имеем снова два случая:
(1) Если Х является головой списка, тогда результатом удаления будет хвост этого списка.
(2) Если Х находится в хвосте списка, тогда его нужно удалить оттуда.
удалить( X, [X | Хвост], Хвост).
удалить( X, [Y | Хвост], [ Y | Хвост1] ) :- удалить( X, Хвост, Хвост1).
как и принадлежит, отношение удалить по природе своей недетерминировано. Если в списке встречается несколько вхождений элемента X, то удалить сможет исключить их все при помощи возвратов. Конечно, вычисление по каждой альтернативе будет удалять лишь одно вхождение X, оставляя остальные в неприкосновенности. Например:
?- удалить( а, [а, b, а, а], L].
L = [b, а, а]; L = [а, b, а]; L = [а, b, а];
nо (нет)
При попытке исключить элемент, не содержащийся в списке, отношение удалить потерпит неудачу.
Отношение удалить можно использовать в обратном направлении для того, чтобы добавлять элементы в список, вставляя их в произвольные места. Например, если мы хотим во все возможные места списка [1, 2, 3] вставить атом а, то мы можем это сделать, задав вопрос: "Каким должен быть список L, чтобы после удаления из него элемента а получился список [1, 2, 3]?"
?- удалить( а, L, [1, 2, 3] ).
L = [а, 1, 2, 3]; L = [1, а, 2, 3]; L = [1, 2, а, 3]; L = [1, 2, 3, а];
nо (нет)
Вообще операция по внесению Х в произвольное место некоторого списка Список, дающее в результате БольшийСписок, может быть определена предложением:
внести( X, Список, БольшийСписок) :- удалить( X, БольшийСписок, Список).
В принадлежит1 мы изящно реализовали отношение принадлежности через конк. Для проверки на принадлежность можно также использовать и удалить. Идея простая: некоторый Х принадлежит списку Список, если Х можно из него удалить:
принадлежит2( X, Список) :- удалить( X, Список, _ ).
3. 2. 5. Подсписок
Рассмотрим теперь отношение подсписок. Это отношение имеет два аргумента - список L и список S, такой, что S содержится в L в качестве подсписка. Так отношение
подсписок( [c, d, e], [a, b, c, d, e, f] )
имеет место, а отношение
подсписок( [c, e], [a, b, c, d, e, f] )
нет. Пролог-программа для отношения подсписок может основываться на той же идее, что и принадлежит1, только на этот раз отношение более общо (см. рис. 3.4).
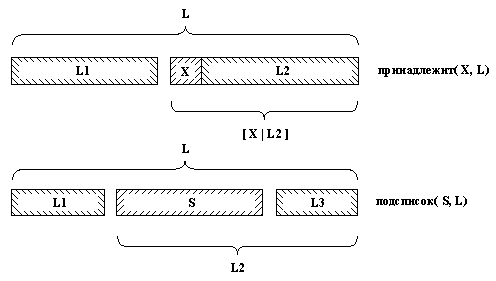
Рис. 3. 4. Отношения принадлежит и подсписок.
Его можно сформулировать так:
S является подсписком L, если
(1) L можно разбить на два списка L1 и L2 и
(2) L2 можно разбить на два списка S и L3.
Как мы видели раньше, отношение конк можно использовать для разбиения списков. Поэтому вышеприведенную формулировку можно выразить на Прологе так:
подсписок( S, L) :- конк( L1, L2, L), конк( S, L3, L2).
Ясно, что процедуру подсписок можно гибко использовать различными способами. Хотя она предназначалась для проверки, является ли какой-либо список подсписком другого, ее можно использовать, например, для нахождения всех подсписков данного списка:
?- подсписок( S, [а, b, с] ).
S = [ ]; S = [a]; S = [а, b]; S = [а, b, с]; S = [b]; . . .